лекции теор. мех (копия). Предмет теоретической механики изучение механического движения и механического взаимодействия материальных тел

• Название: Предмет теоретической механики изучение механического движения и механического взаимодействия материальных тел
• Дата: 29.09.2022
• Размер: 0.97 Mb.
• Имя файла: лекции теор. мех (копия).docx
• Тип: Решение; #704473
• страница: 3 из 4

Пример. Две однородные прямоугольные плиты, сваренные под прямым углом друг к другу, закреплены сферическим шарниром в точке А, подшипником в точке В и невесомым стержнем I (рис 16.2), закреплены на концах шарнирами.

Размеры плит в направлениях, параллельных координатным осям x, y, z, равны соответственно 2а, 3а и 4а, вес большей плиты Р₁=3 кН, вес меньшей плиты Р₂=2 кН. Каждая из плит параллельна одной из координатных плоскостей.

На меньшую плиту действует пара сил с моментом M=4 кН м, лежащая в плоскости плиты, и две силы. Сила F₁ лежит в плоскости, параллельной плоскости xy; по величине F₁=6 кН, приложена в точке D и образует с осями x и y углы 30⁰ и 60⁰ соответственно. Сила F₃, величина которой равна 10 кН, параллельна оси y и приложена в середине стороны плиты.

Определить реакции сферического шарнира А, подшипника В и стержня I, если вся система находится в равновесии, a = 0,6м.

Решение

На плиты, кроме заданных сил P₁, P₂, F₁, F₃ и пары сил с моментом М, действуют реакции связей. Реакцию стержня S₁ направляем вдоль стержня, полагая, что он растянут, реакцию сферического шарнира разлагаем на составляющие X_A, Y_A, Z_A, подшипника на две составляющие Y_B и Z_B в плоскости, перпендикулярной оси подшипника. Имеем произвольную пространственную систему сил.

Составляем уравнения равновесия: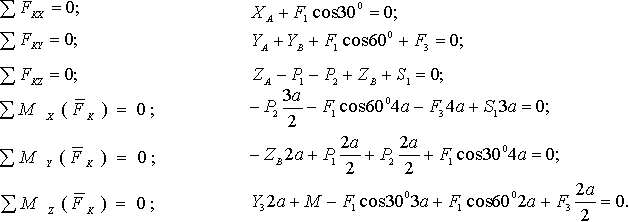

При определении моментов силы F относительно осей разлагаем ее на две составляющие F₁ и F₁, параллельные осям x и y , и применяем теорему Вариньона.

Решая составленные уравнения и подставив числовые значения заданных величин, находим неизвестные.

Получим Х_А = -5 кН, У_А = -9,5 кН, Z_A = -26 кН, У_В=-3,5 кН, Z_В=13 кН, S₁ = 18 кН. Отрицательные знаки у Х_А, У_А, Z_A, У_В указывают, что истинное направление этих составляющих сил реакций противоположно указанному на рисунке.
1. Статически определимые и статически неопределимые системы

При решении задач статики реакции связей всегда являются величинами заранее неизвестными; число их зависит от числа и вида наложенных связей. Условия равновесия, в которые входят реакции связей и которые служат для их определения, называют обычно уравнениями равновесия. Чтобы соответствующая задача статики была разрешимой, надо, очевидно, чтобы число уравнений равновесия равнялось числу неизвестных реакций, входящих в эти уравнения. Задачи, в которых число неизвестных реакций связей равно числу уравнений равновесия, содержащих эти реакции, называются статически определенными, а системы тел (конструкции), для которых это имеет место — статически определимыми. Задачи же, в которых число неизвестных реакций связей больше числа уравнений равновесия, содержащих эти реакции, называются статически неопределенными, а системы тел (конструкции) для которых это имеет место ¦— статически неопределимыми.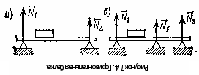

Например, подвеска, состоящая из двух тросов (рис. 7.3, а), будет статически определимой, так как здесь две неизвестные реакции Т₁ и Т₂ войдут в два уравнения равновесия (3.8)) плоской системы сходящихся сил. Подвеска же, состоящая из трех лежащих в одной плоскости тросов (рис. 7.3,б), будет статически неопределимой, так как в ней число неизвестных реакций равно трем (T_l, T₂, Т₃), а уравнений равновесия по-прежнему только два. Аналогично, горизонтальная балка, лежащая на двух опорах (рис. 7.4,а), будет статически определимой, так как и здесь две неизвестные реакции N₁ и N₂ входят в два уравнения равновесия плоской системы параллельных сил. Такая же балка на трех опорах (рис. 7.4, б) будет статически неопределимой.

Рассмотрим еще арку, изображенную на рис. 7.5, а, где связями являются неподвижная шарнирная опора в точке А и шарнирная опора на катках в точке В. Такая арка будет статически определимой, поскольку здесь три неизвестные реакции Х_А, У_А, N_В войдут в три уравнения равновесия 6.2; 6.3; 6.4) произвольной плоской

системы сил. Если же в точке В будет тоже неподвижная шарнирная опора (рис. 7.5, б), то неизвестных реакций окажется четыре (Х_А, Y_A, X_В, Y_B), a уравнений равновесия останется три и арка станет статически неопределимой.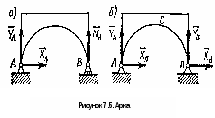

Однако трех-шарнирная арка, изображенная на рис. 7.5, будет статически определимой, так как, расчленив ее в шарнире С на две части, мы введем еще две реакции Х_с, У_с шарнира и неизвестных реакций станет шесть, но и уравнений равновесия тоже шесть (по три для каждой части). С аркой, изображенной на рис. 5,б, так поступить нельзя, поскольку разделив ее на две части, например, сечением, проведенным через точку С, мы получим в этом сечении систему распределенных сил, которую можно привести к двум неизвестным силам Х_с, У_с и паре с неизвестным моментом m_с. Следовательно, неизвестных реакций станет семь ( ) и их из шести уравнений равновесия определить нельзя.

Статическая неопределимость объясняется наложением лишних связей. Например, для обеспечения равновесия балки, изображенной на рис. 7.4, достаточно двух опор и третья опора не нужна (балка считается абсолютно жесткой и не прогибающейся). Статически неопределимые конструкции можно рассчитывать, если учесть их деформации; это делается в курсе сопротивления материалов.

2. 
   Равновесие систем твердых тел.
   

В статике твердого тела наряду с равновесием одного тела рассматриваются сочлененные системы материальных тел, т. е. совокупности твердых тел, касающихся друг друга своими поверхностями или соединенных друг с другом шарнирами, гибкими нитями или стержнями. Важной задачей статики системы твердых тел является определение реакций связей. Для этого основным является способ расчленения, при котором наряду с равновесием всей системы тел рассматривается равновесие отдельных тел (или групп тел системы). При этом все остальные тела системы и соответствующие связи мысленно отбрасываются, а их действие на тело, равновесие которого рассматривается, заменяется реакциями. Следует заметить, что при рассмотрении равновесия всей системы твердых тел реакции связей между телами, входящими в систему, не должны учитываться; они не входят в уравнения равновесия, как внутренние, взаимно уравновешенные силы. А при рассмотрении равновесия каждого тела в отдельности или какой-либо группы тел, входящих в систему, соответствующие реакции связей, которые были мысленно расчленены, становятся внешними силами и входят в уравнения равновесия.

При решении задач на равновесие системы тел недостаточно, как правило, рассмотреть равновесие этой системы в целом. Для всей системы условия равновесия сводятся или к трем уравнениям равновесия для плоской системы сил, или к двум уравнениям для плоской системы параллельных сил. В этом случае число неизвестных может быть больше числа перечисленных уравнений. Однако это обстоятельство еще не делает систему статически неопределимой, так как если разделить систему на отдельные твердые тела и составить уравнения равновесия для каждого из них, то число новых неизвестных может быть меньше числа новых уравнений равновесия. Если число всех составленных таким образом независимых уравнений равновесия для всей системы и отдельных ее частей будет равно числу всех неизвестных, то такая задача является статически определенной.

При решении задач па равновесие твердых тел надо:

1) выделить твердое тело, равновесие которого надо рассмотреть для отыскания неизвестных величин;

2) изобразить активные силы;

3) если твердое тело несвободно, то, примени» закон освобождаемости от связей, приложить к нему соответствующие реакции связей;

4) рассмотреть равновесие данного несвободного твердого тела, как тела свободного, находящегося под действием активных сил и реакций связей;

5) сопоставить число неизвестных величин и число независимых уравнений равновесия; эти числа должны быть равны, если задача является статически определенной;

6) выбрать наиболее удобные системы координат; при этом для каждого тела и для всей системы тел может быть избрана своя система координат;

7) составить уравнения равновесия для каждого твердого тела или для каждой системы твердых тел, равновесие которых исследуется;

8) решить систему всех уравнений равновесия.
Если система твердых тел разделяется па отдельные тела, то при замене их взаимодействия реакциями связей следует ввести реакции, приложенные к одному телу, и на основании закона равенства действия и противодействия выбрать реакции, действующие па второе тело, равными по модулю и направленными прямо противоположно

В том случае, когда значение неизвестной силы окажется по ответу отрицательным, направление этой силы следует взять противоположным тому, которое было изображено на рисунке. При составлении уравнений равновесия целесообразно оси координат и точки, относительно которых составляются уравнения моментов сил, выбирать так, чтобы в каждое уравнение входила только одна неизвестная величина. Если по условию задачи требуется определить лишь некоторые неизвестные величины, то надо составить только те из уравнений равновесия, которые необходимы для получения ответа.

2. 
   Силы и нагрузки используемые при решении задачи.
   

Сосредоточенные силы. Сосредоточенными считаются силы, приложенные к малой поверхности, размеры которой малы по сравнению с размерами тела. Однако при расчете напряжений вблизи зоны приложения силы нагрузку следует считать распределенной. К сосредоточенным нагрузкам относят не только сосредоточенные силы, но и пары сил, примером которых можно счи­тать нагрузку, создаваемую гаечным ключом при закручивании гайки. Сосредоточенные усилия измеряются в кН.

Распределенные нагрузки. В инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности по тому или иному закону. Рассмотрим некоторые простейшие примеры распределенных сил, лежащих в одной плоскости. Плоская система распределенных сил характеризуется ее интенсивностью q, т. е. значением силы, приходящейся на единицу длины нагруженного отрезка. Измеряется интенсивность в ньютонах, деленных на метры (Н/м).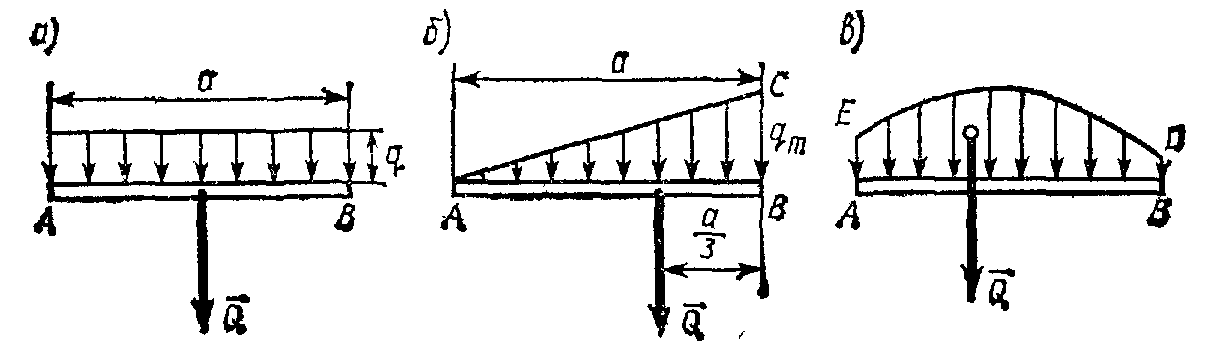



Рисунок 7.1. Распределенные нагрузки.
Примеры распределенных нагрузок.

1) Силы, равномерно распределенные вдоль отрезка прямой (рис. 7.1, а). Для такой системы сил интенсивность q имеет постоянное значение. При статических расчетах эту систему сил можно заменить равнодействующей Q

По модулю,

Q=aq.

Приложена сила Q в середине отрезка АВ.

2) Силы, распределенные вдоль отрезкапрямой по линейному закону (рис. 7.1, б). Примером такой нагрузки могут служить силы давления воды на плотину, имеющие наибольшее значение у дна и падающие до нуля у поверхности воды. Для этих сил интенсивность q является величиной переменной, растущей от нуля до максимального значения q_m. Равнодействующая Q таких сил определяется аналогично равнодействующей сил тяжести, действующих на однородную треугольную пластину ABC. Так как вес однородной пластины пропорционален ее площади, то, по модулю,



Приложена сила Q на расстоянии, а/3 от стороны ВС треугольника ABC.

3) Силы, распределенные вдоль отрезка прямой по произвольному закону (рис. 7.1, в).

Равнодействующая Q таких сил, по аналогии с силой тяжести, по модулю равна площади фигуры ABDE, измеренной в соответствующем масштабе, и проходит через центр тяжести этой площади (вопрос об определении центров тяжести площадей будет рассмотрен

Реакция жесткой заделки. Особая связь. Эта связь препятствует не только линейным перемещениям закрепленной точки тела, но и повороту вокруг этой точки. Реакцией такой опоры являются неизвестная по величине и направлению сила R_A с углом α (или X_A и Y_A) и момент Μ_A (рис. 7.2).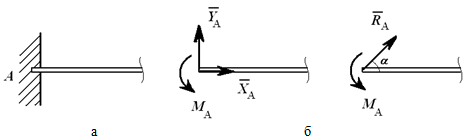



Рисунок 7.2. Жесткая (полная) заделка.

3. Задачи.

Задача 1. Определить опорные реакции системы, состоящей из двух балок, сочлененных идеальным шарниром, если Р1==10 Т, Р2 = 6 Т, а = 2 м. Конец А балки АС защемлен, конец В балки СВ укреплен в катковой опоре (рис. 7.6, а).

На рисунке 7.6, а число не известных (реакций) – четыре. Задача плоская, система сил произвольная. Количество уравнений равновесия плоской произвольной системы сил – три. Значит задача статический неопределима.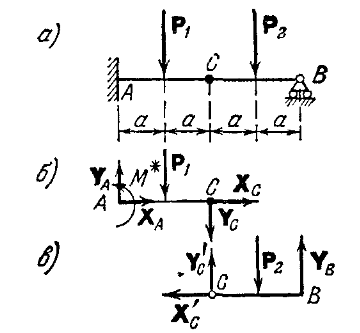



Рисунок 7.6. Равновесие систем одномерных твердых тел.
Рассмотрим равновесие каждой балки в отдельности. Мы получаем два твердых тела, на которые действуют реакции внешних связей Х_А, У_А, М*, Y_В И попарно равные силы взаимодействия Хс=— Х^, Yc= — У'с. Таким образом общее число неизвестных равно шести. Запишем уравнения равновесия для левой балки (рис. 7.6, б):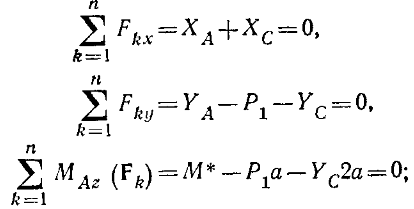



для правой балки (рис. 7.6, в):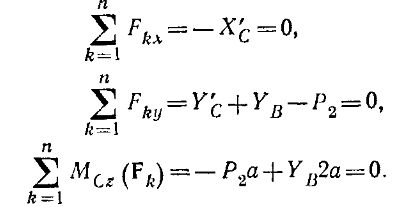



Ha основании аксиомы 4 (третьего закона Ньютона) модули сил Х_с и Х'_С а также сил Y_c и Y'_c, равны между собой, т. е Х_С=Х'_С и Y_C = Y'_C. Учитывая эти равенства и решая затем полученную систему уравнений, находим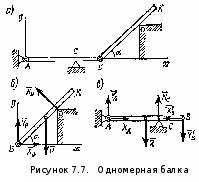


Задача 2. Горизонтальная балка А В весом Q=200 H прикреплена к стене шарниром А и опирается yа опoру С (рис. 7.7, а). К ее концу В шарнирно прикреплен брус ВК весом Р=400 Н, опирающийся на выступ В. При этом СВ=АВ/3,

DK=BK/3, угол α=45°. Определить реакции опор, считая балку и брус однородными.

Решение. Расчленяя систему на две части, рассматриваем равновесие

бруса ВК и балки АВ в отдельности. На брус ВК, (рис. 2,б) действуют сила и реакции связей 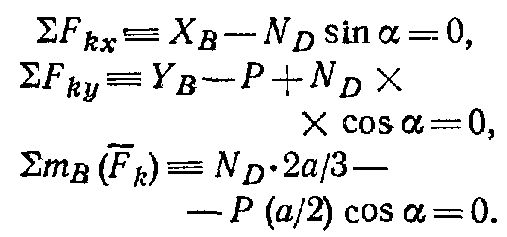Вводя обозначение ВК=а и составляя для этих сил условия равновесия), получим:




Решая эти уравнения, найдем: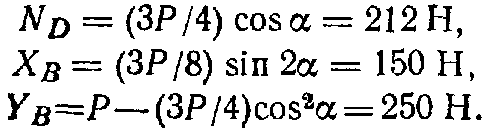



На балку АВ, если ее рассматривать отдельно, действуют сила реакции внешних связей и силы давления бруса ВК, передаваемые через шарнир В (рис. 4.5, в). При этом по закону о действии и противодействии силы должны быть направлены противоположно