1ОргЭвмИС лаб2. ОргЭвмиС лаб2. Представление информации в эвм
 Скачать 179.97 Kb. Скачать 179.97 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра Вычислительной техники отчет по лабораторной работе №2 по дисциплине «Организация ЭВМ и систем» Тема: Представление информации в ЭВМ
Санкт-Петербург 2020 ЦЕЛЬ: Изучение машинного языка. Задание 1. Для изучения структуры двух команд (MOV и ADD), в которых используются непосредственные данные, выполним следующий код: MOV AX,4629h ;в AX записывается шестнадцатеричное число 4629 ADD AX,036Ah ;к числу записанному в AX прибавляется 036А, результат ;сохраняется в AX 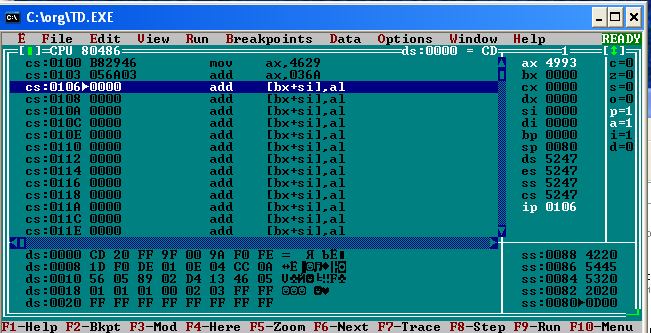 Задание 2. Для понимания правил, по которым компьютер обеспечивает доступ к данным посредством регистров SI, DI, DS, выполняем следующий код: MOV SI,3 ;записываем в SI, 0003 MOV DI,8 ;записываем в DI, 0008 MOV AX,2100 ;записываем в AX 2100, чтобы потом записать AX в DX MOV DX,AX ;т.к. в DX нельзя занести численное значение сразу же MOV byte ptr [0003], 7Ch ;в сегменте данных по адресу 0003 размещаем число 7C MOV AL,[SI] ;в AL (нижняя часть AX) записываем значение по адресу в SI MOV [DI],AL ;по адресу в DI, записываем значение из AL 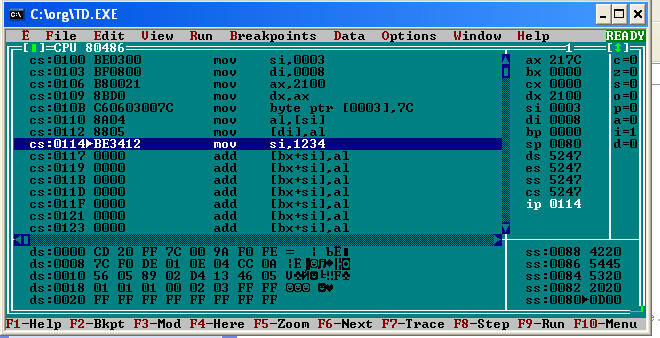 Задание 3. Для изучения способа кодирования символов представим в памяти процессора строку символов (имя и год рождения): DS:0000 41 72 74 65 6В 39 39 00 A r t e m 9 9 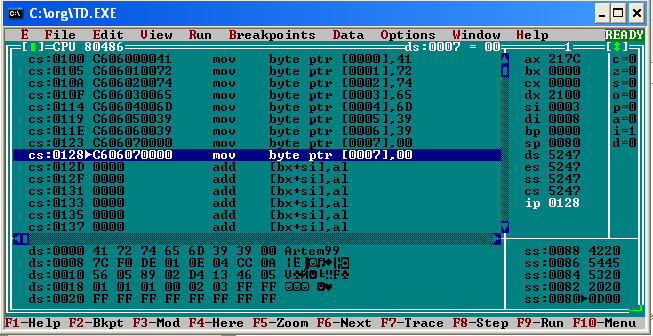 Задание 4. Для изучения машинного (двоичного) представления целой и дробной частей числа в формате с фиксированной запятой, выполним следующий код: MOV AX,1080h ;записываем в AX 1080 MOV BX,1240h ;записываем в BX 1240 ADD AX,BX ;складываем AX + BX, результат записывается в AX В AX будет значение 22С0h. Флаг чётности P изменит значение с 0 на 1 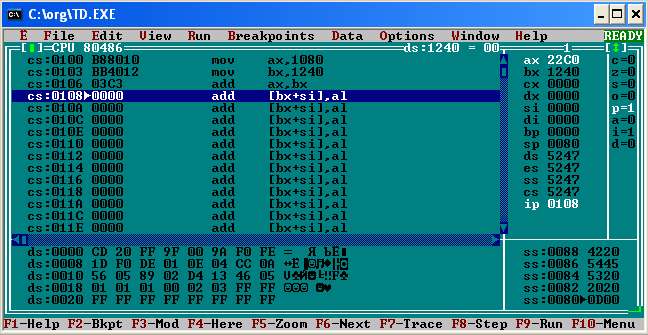 Задание 5. Для изучения машинного (двоичного) представления коротких вещественных чисел, задаваемых в формате с плавающей точкой, напишите и выполните фрагмент программы, заданный ниже. FINIT ; инициализация математического сопроцессора FPU FLDZ ; в вершину стека записывается значение 0.0 FLD1 ; в вершину стека записывается 1.0 FADD ST,ST(1) ;сложение верхнего числа в стеке с следующим за ним ;т.е. 1.0 + 0.0 Результат сохраняется в вершине стека FST dword ptr[0] ;Копирование вершины стека в сегмент данных по адресу 0000 ;dword ptr – 4 байта FLD1 ;в вершину стека записывается 1.0 FADD ST,ST(1) ; сложение верхнего числа в стеке с следующим за ним ; т.е. 1.0 + 1.0 Результат сохраняется в вершине стека FST dword ptr[4] ;копирование вершины стека в ds:0004 FLD1 ;в вершину стека записывается 1.0 FADD ST,ST(1) ;сложение верхнего числа в стеке с следующим за ним т.е. 2.0 + 1.0 Результат сохраняется в вершине стека FST dword ptr[8] ;копирование вершины стека в ds:0008 FLD1 ;в вершину стека записывается 1.0 FADD ST,ST(1) ;сложение верхнего числа в стеке с следующим за ним ; т.е. 3.0 + 1.0 Результат сохраняется в вершине стека FST dword ptr[0c] ;копирование вершины стека в ds:0008 FDIVR ST,ST(2) ; вещественной число ½ размещено в вершине стека. ;FDIVR - Деление вещественное реверсивное FST dword ptr[10] ; копирование вершины стека в ds:0010 Скриншот исходного состояния: 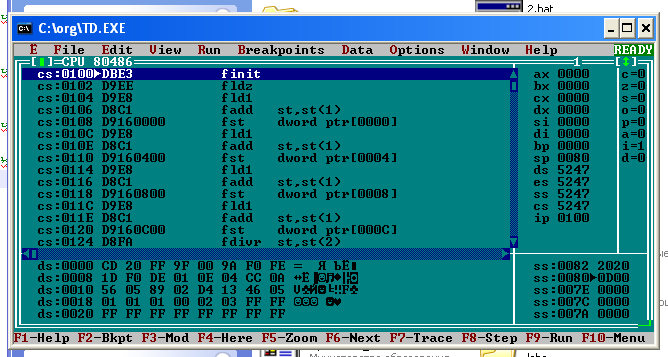 Скриншот конечного состояния: 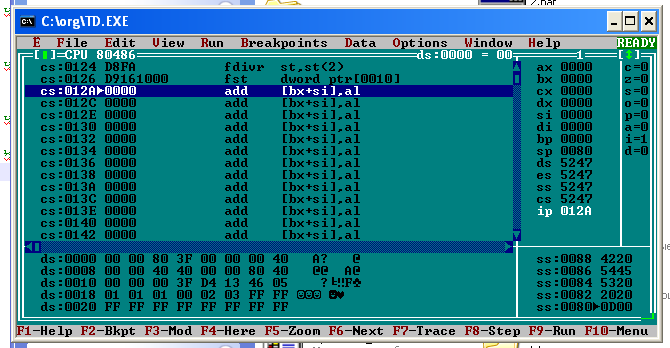 В результате в сегменты памяти заносятся следующие значения: ds:0000 00 00 80 3F 00 00 00 40 ds:0004 00 00 00 40 00 00 40 40 ds:0008 00 00 40 40 00 00 80 40 ds:000C 00 00 80 40 00 00 00 3F ds:0010 00 00 00 3F D4 13 46 05 Переводим эти числа в двоичную систему счисления: 3F 80 00 0016 = 0011 1111 1000 0000 0000 00002 40 00 00 0016 = 0100 0000 0000 0000 0000 00002 40 40 00 0016 = 0100 0000 0100 0000 0000 00002 40 80 00 0016 = 0100 0000 1000 0000 0000 00002 Знак числа Порядок Мантисса          0 011 1111 1000 0000 0000 00002
(цифры мантиссы)*2^(P-127) P-порядок. 0011 1111 1000 0000 0000 0000 = 1,0*2^128-127=1 0100 0000 0000 0000 0000 0000 = 1,0*2^128-127=2 0100 0000 0100 0000 0000 0000 = 1,1*2^128-127=3 0100 0000 1000 0000 0000 0000 = 1,0*2^128-127=0,5 Выводы по лабораторной работе: Команда MOV - пересылка данных между регистрами или регистрами и памятью. Работает с двумя операндами. Данные пересылаются из второго в первый операнд. В регистр dx нельзя положить непосредственное значение. Нужно использовать промежуточный регистр. Данная команда не изменяет регистр флагов. Команда ADD - сложение двух операндов источник и приемник размерностью байт, слово или двойное слово. Результат записывается в первый операнд. Данная команда изменяет регистр флагов. Арифметический сопроцессор предназначен для выполнения операций над числами в формате с плавающей точкой (вещ. числа) и длинными целыми числами. Он значительно ускоряет вычисления, связанные с вещ. числами. Стек - специально выделенная область памяти для передачи или сохранения данных. Верхний стек имеет адрес 0, нижний – 28. При записывании нового числа оно помещается в стек с адресом ноль (ST(0)). Число с плавающей точкой представляется в виде: (знак)(мантисса)E(знак)(порядок). Для перевода числа в формат с плавающей точкой нужно: перевести число в двоичную форму, где первый бит показывает знак числа, последующие восемь его порядок, оставшиеся – мантиссу; затем воспользоваться формулой: (1). Арифметический сопроцессор работает с нормализованными числами, поэтому поле мантиссы содержит мантиссу нормализованного числа (1). |
