|
|
Преподаватель Т. Н. Мурылева Задание на период с 13. 04 17. 04. 2020 г
Преподаватель Т.Н. Мурылева
Задание на период с 13.04 – 17.04.2020 г.
Электронная почта tatjana_15_1976@mail.ru
Курс
|
группа
|
дисциплина
|
задание
|
1
|
ССА-11
ССА-12
МТО-11
|
Математика
|
Изучить лекцию и переписать в тетрадь. (лекцию переписать в тетрадь, пересылать не надо, проверю после карантина )
Действия с векторами. Разложение вектора на составляющие.
Откладывание вектора, равного данному.
От любой точки плоскости можно отложить единственный вектор, равный данному. Построение вектора 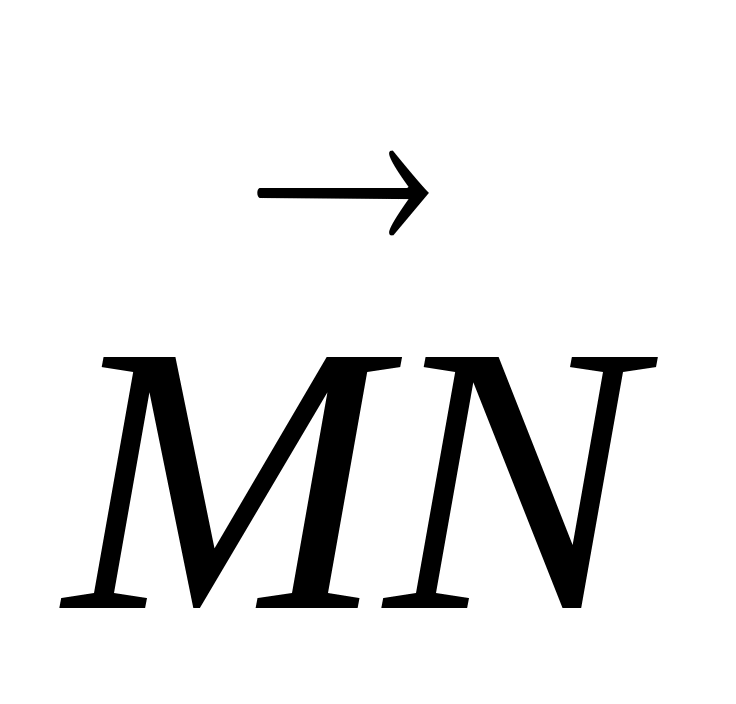 , равного вектору , равного вектору  , называют откладыванием вектора , называют откладыванием вектора  от точки М. Для этого через точку М проведем прямую p, параллельную вектору от точки М. Для этого через точку М проведем прямую p, параллельную вектору  . На прямой p отложим векторы . На прямой p отложим векторы 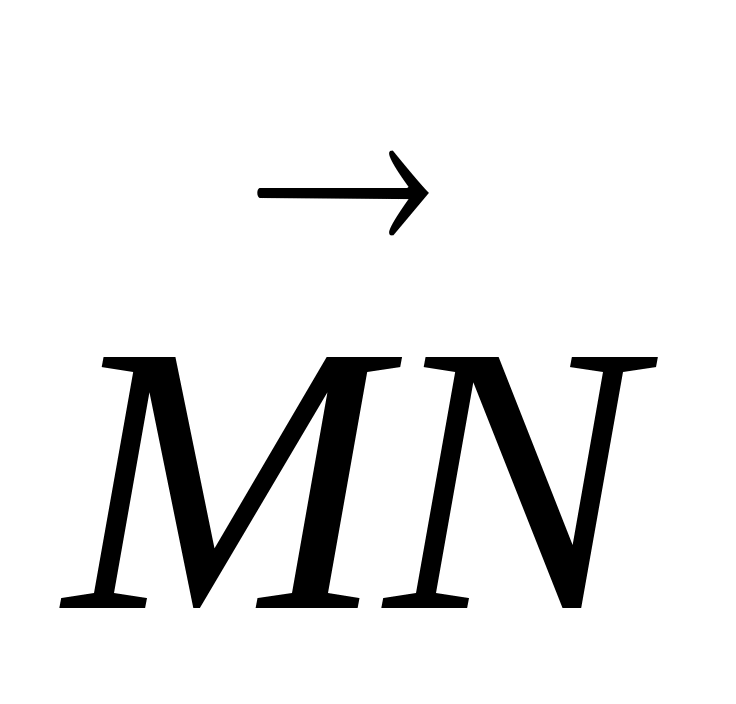 и и 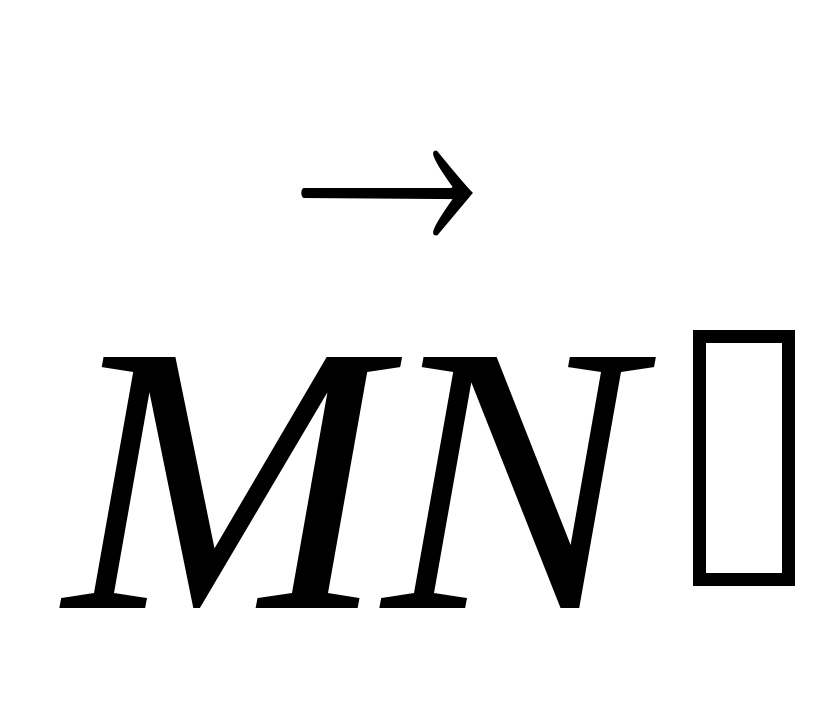 , равные вектору , равные вектору  и из двух векторов и из двух векторов 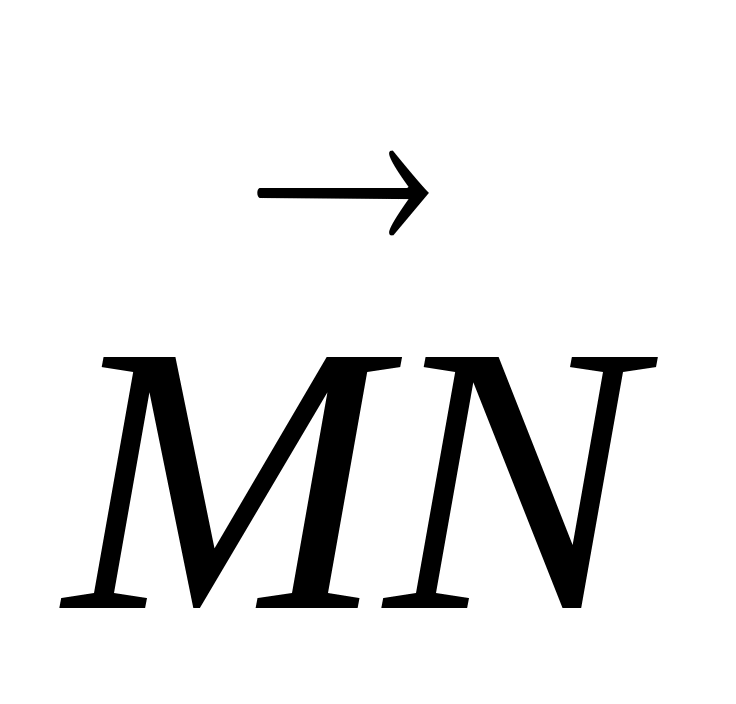 и и  выберем тот, который сонаправлен с вектором выберем тот, который сонаправлен с вектором  . .
Сложение векторов.
Пусть  и и  - два вектора. Отметим произвольную точку А и отложим от этой точки вектор - два вектора. Отметим произвольную точку А и отложим от этой точки вектор 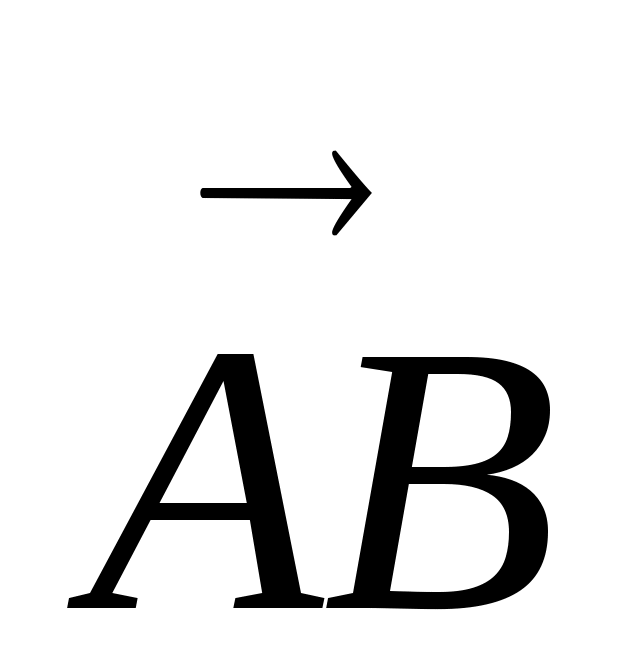 , равный вектору , равный вектору  .Затем от точки В отложим вектор .Затем от точки В отложим вектор  , равный вектору , равный вектору  . Вектор . Вектор 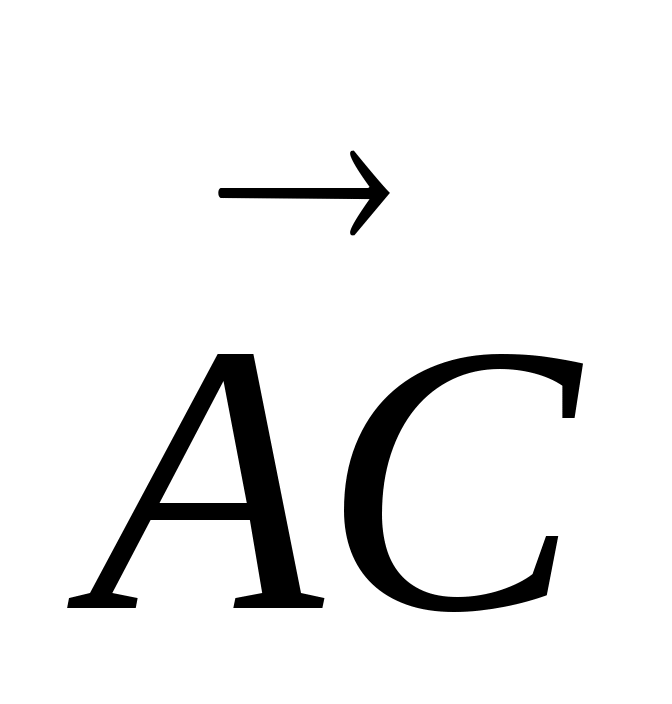 называется суммой векторов называется суммой векторов  и и  . Этот способ сложения векторов называется правилом треугольника. . Этот способ сложения векторов называется правилом треугольника.
Сумму векторов можно найти другим способом - по правилу параллелограмма. От произвольной точки О откладываем векторы 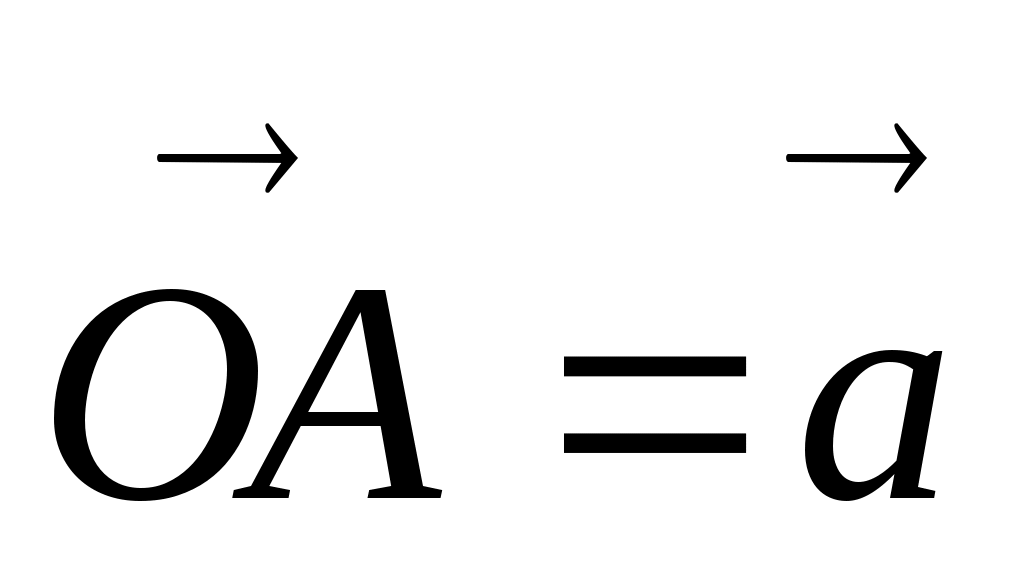 и и
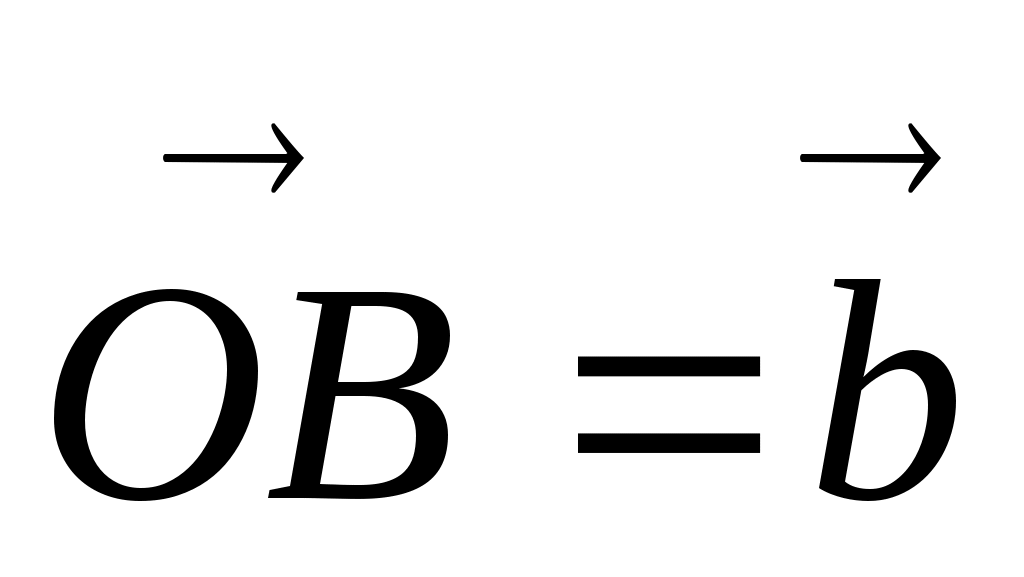 . Достраиваем до параллелограмма OABC. Тогда вектор . Достраиваем до параллелограмма OABC. Тогда вектор 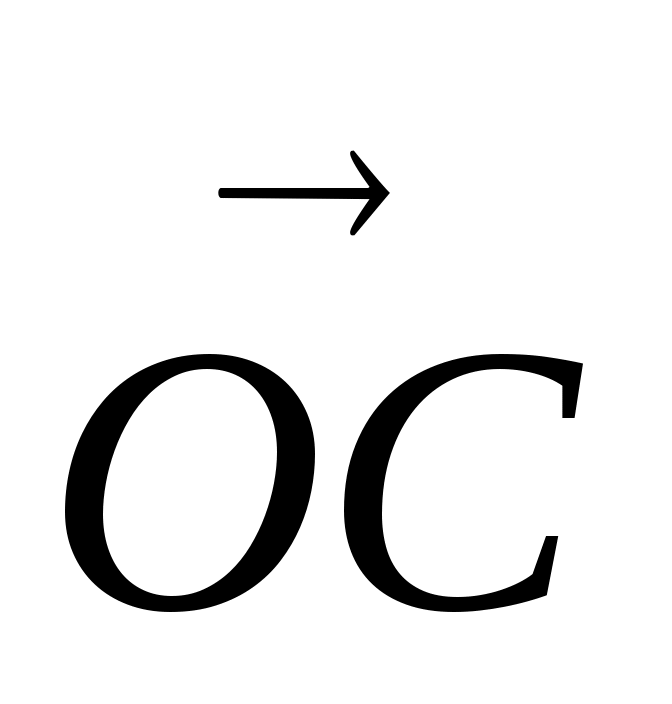 , где ОС – диагональ параллелограмма является суммой векторов , где ОС – диагональ параллелограмма является суммой векторов  и и 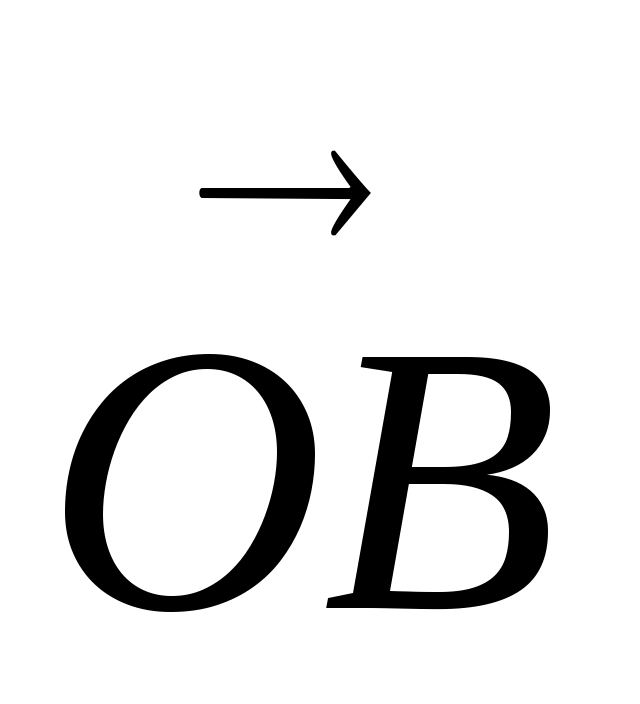 . .
Для того, чтобы сложить больше чем два вектора. От произвольной точки О откладывают первый вектор, от конца первого вектора откладывают второй вектор, от конца второго вектора - третий вектор и т. д. Суммой будет являться вектор, начало которого совпадает с началом первого вектора, а конец – с концом последнего. Данный способ сложения называется правилом многоугольника.
Вычитание векторов.
Вектор противоположный вектору  , обозначают , обозначают  . Два вектора называются противоположными, если их сумма равна нулевому вектору. Чтобы вычесть из вектора . Два вектора называются противоположными, если их сумма равна нулевому вектору. Чтобы вычесть из вектора  вектор вектор  , достаточно к вектору , достаточно к вектору  прибавить вектор, противоположный вектору прибавить вектор, противоположный вектору  , т. е. , т. е. 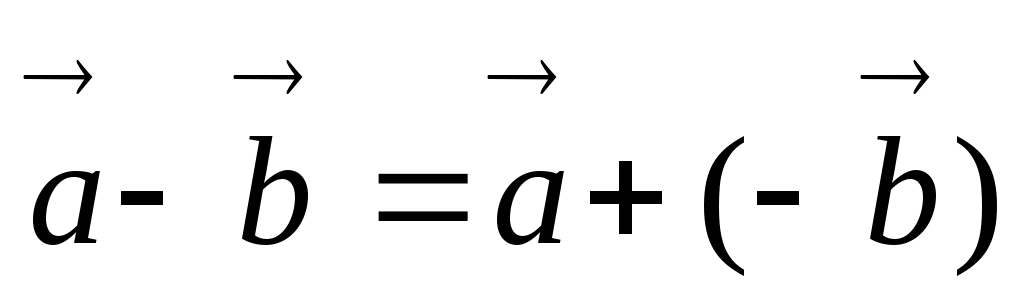 . .
Умножение вектора на число.
Произведением ненулевого вектора  на число m называется вектор, сонаправленный с вектором на число m называется вектор, сонаправленный с вектором  , если m>0; противоположно направленный, если m<0. Длина этого вектора равна произведению длины вектора , если m>0; противоположно направленный, если m<0. Длина этого вектора равна произведению длины вектора  на модуль числа m. на модуль числа m.
Домашнее задание. (по желанию. Кто не сделает оценку «2» не поставлю. Кто разберется с темой домашнюю работу делает самостоятельно и добросовестно).
1. Дан вектор  , длина которого равна 6 см. Построить векторы: , длина которого равна 6 см. Построить векторы:

2. Начертите два произвольных неколлинеарных вектора  и и  . Постройте . Постройте

3. Дан параллелограмм ADCD, диагонали которого пересекаются в точке О. Через векторы  и и 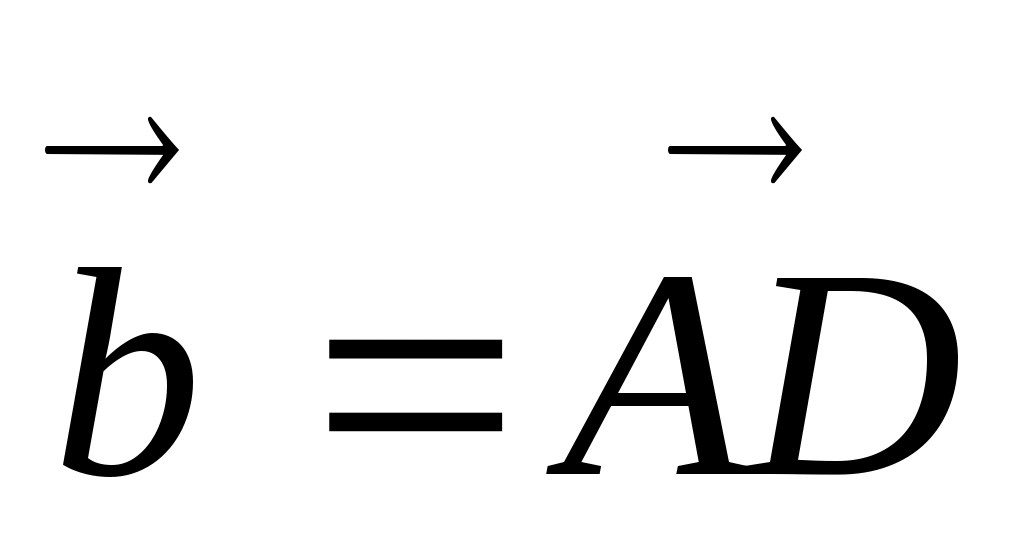 выразить векторы: выразить векторы:
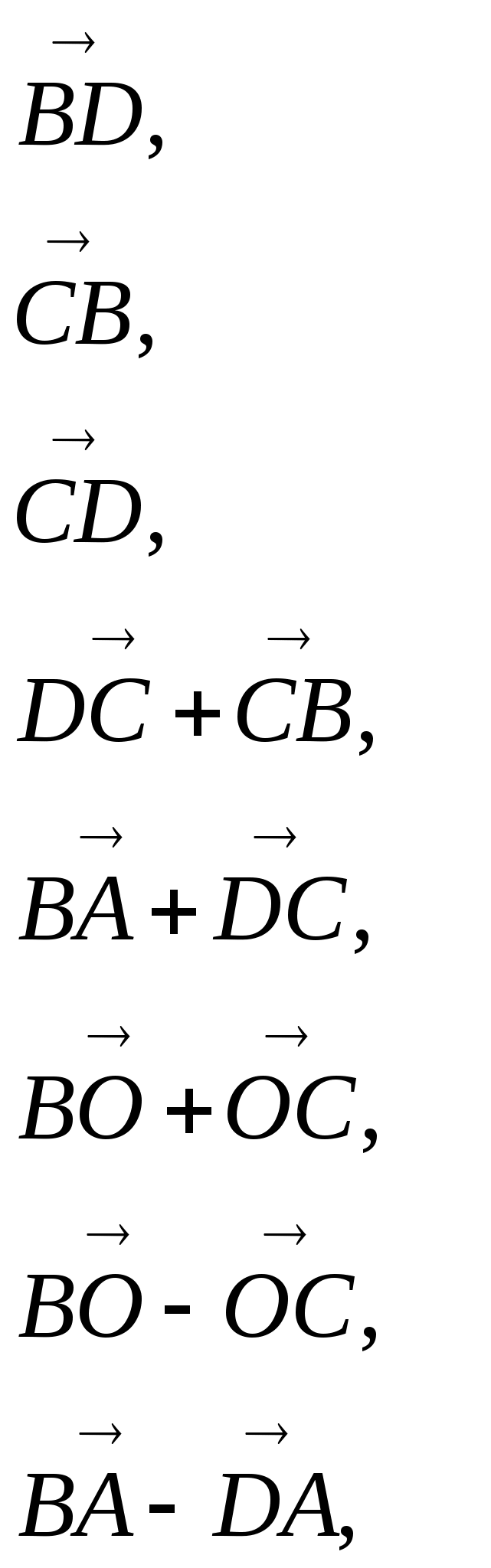
|
2
|
ССА-21
|
Элементы высшей математики
|
Практическая работа по теме: «Исследование функции и построение графиков»
1 вариант - Андронов, Бочкун, Гребенников, Задков, Калмыков, Кондидатов, Погосян, Скачков, Лопатко, Морозов, Писакина, Щипакин
2 вариант – Атаева, Гетьманенко, Гурьянов, Килочко, Куклинский, Куховаренко, Лопастейский, Малахов, Овсянников, Пронин, Розин, Трифонов
ВАРИАНТ 1
|
ВАРИАНТ 2
|

|
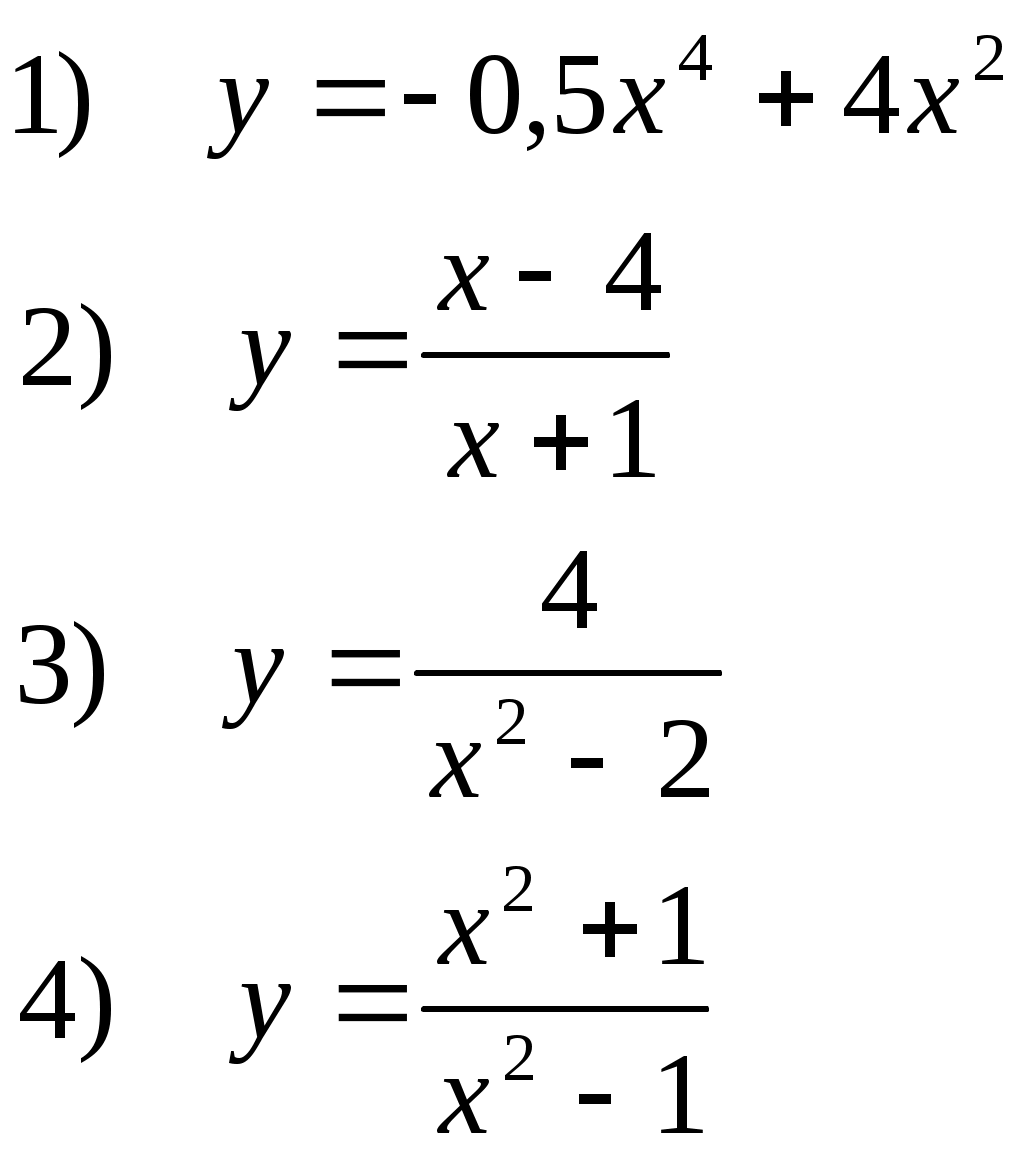
|
1) и 2) задания - правильно решенные на оценку «3»
1) - 3) задания - правильно решенные на оценку «4»
1) - 4) задания - правильно решенные на оценку «5»
Тема: Общая схема исследования функции.
1. Найти область определения функции.
2. Выяснить вопрос о четности и нечетности функции.
Функция y=f(x) называется четной, если f(-x)=f(x). График четной функции симметричен относительно оси ординат.
Функция y=f(x) называется нечетной, если f(-x)=-f(x). График нечетной функции симметричен относительно начала координат.
Остальные функции являются не четными, не нечетными.
3. Найти точки пересечения графика с осью Оу (при этом х=0) .
Найти точки пересечения графика с осью Ох (у=0) и интервалы знакопостоянства функции.
Интервалы, в которых данная функция принимает только положительные или только отрицательные значения, называются интервалами знакопостоянства этой функции. Для определения таких интервалов нужно:
а) найти точки разрыва функции;
б) найти точки пересечения графика этой функции с осью абсцисс (Ох);
в) определить знак функции в каждом из интервалов, на которые полученные в пунктах а) и б) точки разобьют область определения функции.
4. Найти интервалы возрастания и убывания функции и экстремальные точки.
Функция называется возрастающей на некотором промежутке, если большему значению аргумента соответствует большее значение функции. Возрастание дифференцируемой функции y=f(x) характеризуется тем, что f’(x)>0.
Функция называется убывающей на некотором промежутке, если большему значению аргумента соответствует меньшее значение функции. Убывание дифференцируемой точки y=f(x) характеризуется тем, что f’(x)<0.
Значение f(x0) функции y=f(x) в точке x= x0 называется максимумом, если оно больше, чем значения этой функции во всех точках, достаточно близких к x0. Сама точка x= x0 в этом случае называется точкой максимума. Точки максимума дифференцируемой функции характеризуются тем, что знак производной при переходе через такую точку меняется с + на -, а значение производной в самой точке равно нулю или не существует.
Значение f(x0) функции y=f(x) в точке x= x0 называется минимумом, если оно меньше, чем значения этой функции во всех точках, достаточно близких к x0. Сама точка x= x0 в этом случае называется точкой минимума. Точки минимума дифференцируемой функции характеризуются тем, что знак производной при переходе через такую точку меняется с - на +, а значение производной в самой точке равно нулю или не существует.
Правило для определения экстремумов функции y=f(x) и интервалов ее возрастания и убывания с помощью первой производной:
а) найти первую производную f’(x);
б) найти критические точки первого рода: точки, в которых производная равна нулю или не существует;
в) определить знак первой производной в каждом из интервалов, на которые найденные критические точки разобьют область определения данной функции, и тем самым найти интервалы возрастания и убывания функции.
г) определить, какие из критических точек являются экстремальными (какие точками максимума и какие точками минимума).
д) вычислить значения функции в найденных экстремальных точках и таким образом определить искомые экстремумы.
5. Найти интервалы выпуклости и вогнутости графика функции и точки перегиба.
Выпуклость графика дважды дифференцируемой функции y=f(x) характеризуется тем, что f˝′(x)<0. Вогнутость графика дважды дифференцируемой функции y=f(x) характеризуется тем, что f˝′(x)>0. Точка х=х0 называется точкой перегиба функции y=f(x), если при переходе аргумента х через эту точку график функции меняет вогнутость на выпуклость или на наоборот. Точка перегиба дважды дифференцируемой функции характеризуются тем, что при переходе через такую точку меняет знак второй производной, а значение производной в самой точке равно нулю или не существует.
Правило для нахождения интервалов выпуклости и вогнутости и точек перегиба функции y=f(x):
а) найти вторую производную f˝′(x).
б) найти критические точки второго рода: точки, в которых вторая производная равна нулю или не существует.
в) определить знак второй производной f˝′(x) в каждом из интервалов, на которые найденные критические точки разобьют область определения данной функции, и тем самым найти интервалы выпуклости и вогнутости.
г) определить, какие из критических точек являются точками перегиба.
д) вычислить значения функции в найденных точках перегиба.
6. Найти уравнения асимптот.
Различают три вида асимптот:
а) Горизонтальная.
Прямая у=b называется горизонтальной асимптотой. Для нахождения данной асимптоты необходимо вычислить предел данной функции при  . Асимптота, существует, если данный предел равен какому-либо числу. . Асимптота, существует, если данный предел равен какому-либо числу.
б) Вертикальная.
Прямая х=а называется вертикальной асимптотой. Вертикальная асимптота существуют у дробно-рациональных функций (это те значения переменной х, при которых знаменатель обращается в нуль).
в) Наклонная.
Прямая y=k*x+b называется наклонной асимптотой.
Коэффициент k находится по формуле k= , а число , а число  . .
7. Построить график функции, используя все собранные данные.
|
2
|
ССА-21
|
Дискретная математика
|
Изучить лекцию и переписать в тетрадь.
Тема: Алгебра логики. Понятие высказываний. Логические операции над высказываниями.
Алгебра логики (булева алгебра) - это раздел математики, изучающий высказывания, рассматриваемые со стороны логических значений: истинности или ложности и логических операций над ними.
Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать истинно оно или ложно, но не то и другое вместе. Повелительные, вопросительные и бессмысленные предложения не являются высказываниями.
Пример: «6 – четное число» - истинное; «Рим – столица Франции» - ложное.
Истинность или ложность предложения, которую мы приписываем высказыванию и есть истинностное значение высказывания. Часто истинность обозначается: и, Т, 1; а ложность - л, F, 0.
Не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения «Ученик девятого класса», «Информатика – интересный предмет». Такие предложения называются высказывательными формами. Алгебра логики рассматривает любое высказывание только с одной точки зрения – является ли оно истинным или ложным.
Логические высказывания бывают двух видов:
Элементарные (простые) – представляют собой одно утверждение и не зависят от других высказываний, например «Иванов - учитель».
Составные (сложные) – это высказывания образованные из простых высказываний с помощью логических связок «И», «НЕ», «ИЛИ», «ЕСЛИ…ТО», «ТОГДА И ТОЛЬКО ТОГДА, КОГДА». Истинность или ложность получаемых сложных высказываний зависит от истинности или ложности элементарных высказываний, входящих в состав сложного.
Простые высказывания называются логическими переменными, а сложные - логическими функциями этих переменных. Простые логические высказывания обозначают маленькими буквами латинского алфавита, а составные – заглавными.
Логические операции записывают в таблицах истинности, в которых отражаются результаты вычислений сложных высказываний при различных значениях исходных простых высказываний.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет своё название и обозначение:
1. Логическое умножение (конъюнкция) - это объединение двух или нескольких высказываний в одно с помощью союза «И».
Обозначается *,  , &. , &.
Сложное высказывание, образованное в результате конъюнкции истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.
Таблица истинности для двух переменных имеет вид:
-
х
|
у
|
х у у
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
2. Логическое сложение (дизъюнкция) – объединение двух или нескольких высказываний в одно с помощью союза «ИЛИ».
Обозначается +,  . .
Сложное высказывание, образованное в результате логического сложения истинно тогда и только тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
Таблица истинности для двух переменных имеет вид:
-
х
|
у
|
х у у
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
Примечание: Следует выделить строгую дизъюнкцию (исключающее ИЛИ, сумма по модулю 2, сумма Жегалкина)– это понимание связки «ИЛИ» , которое исключает одновременную истинность обоих высказываний (или А, или В, но не оба вместе). Обозначается  , XOR. , XOR.
-
х
|
у
|
х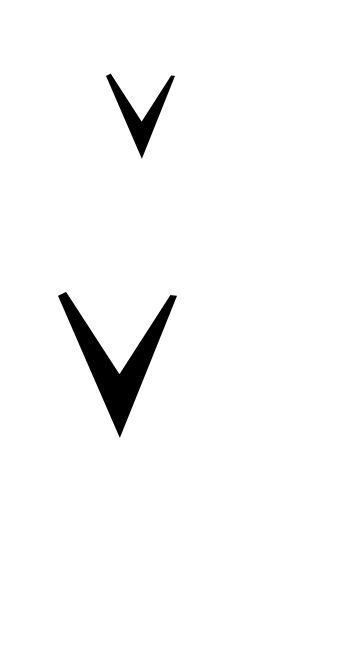 у у
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
3. Логическое отрицание (инверсия).
Присоединение частицы «НЕ» к простому высказыванию называется операцией логического отрицания или инверсией первоначального предложения.
Обозначается:  . .
Инверсия делает истинное высказывание ложным, а ложное – истинным.
Таблица истинности имеет вид:
-
х
|
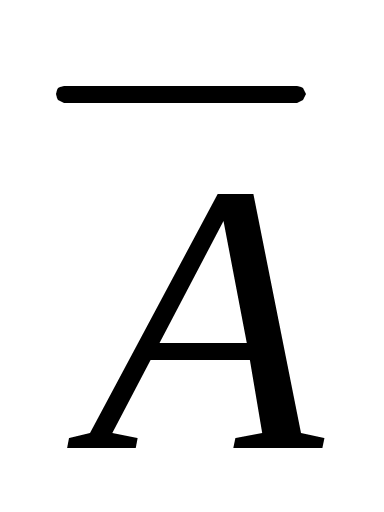
|
0
|
1
|
1
|
0
|
4. Импликация.
Это логическая операция, выражаемая связками «ЕСЛИ…ТО..», «ИЗ….СЛЕДУЕТ».
Обозначается: →.
Высказывание х→у ложно тогда только тогда, когда х – истинно, а у – ложно.
Таблица истинности для двух переменных имеет вид:
-
х
|
у
|
х→у
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
5. Эквиваленция.
Логическая операция, выражаемая связками «НЕОБХОДИМО И ДОСТАТОЧНО», «ТОГДА И ТОЛЬКО ТОГДА, КОГДА».
Обозначается: , ↔.
Высказывание х↔у истинно тогда только тогда, когда значения х и у совпадают.
Таблица истинности для двух переменных имеет вид:
-
х
|
у
|
х↔у
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
Примечание. Высказывания х и у образующие составное высказывание х↔у , могут быт совершенно не связаны по содержанию. Например: х – «3 больше 2», у – «пингвины живут в Антарктиде».
Если в логической формуле присутствует сразу несколько операций, то выполняют их в следующем порядке:
круглые скобки;
отрицание;
конъюнкция;
дизъюнкция;
импликация.
Таблица истинности логической формулы выражает соответствие между всевозможными значениями переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений четыре:
00 01 10 11
Если формула содержит три переменные, то наборов восемь:
000 001 010 011 100 101 110 111
Если формула содержит четыре переменных, то наборов шестнадцать:
-
0000
0001
0010
0011
|
0100
0101
0110
0111
|
1000
1001
1010
1011
|
1100
1101
1110
1111
|
Домашнее задание.
Задания. Построить таблицы истинности: 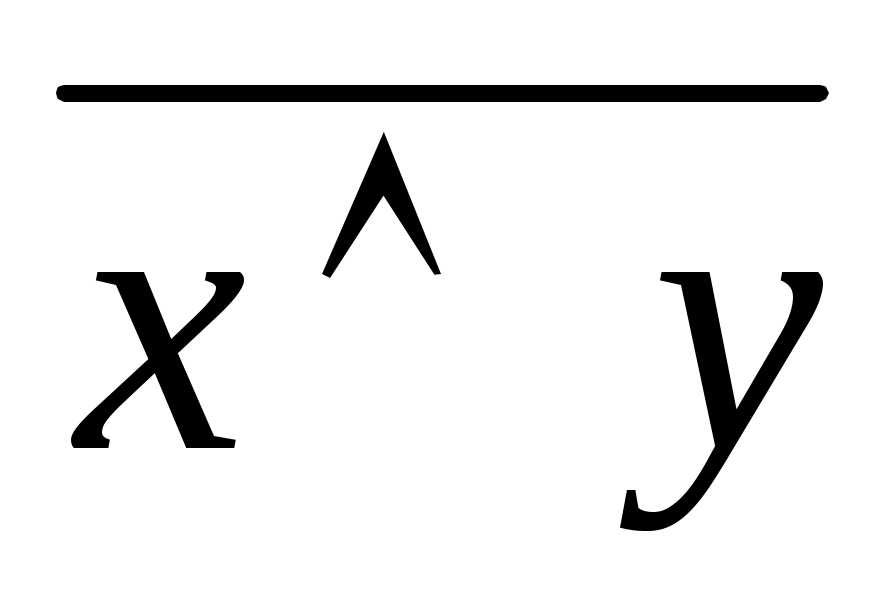 , , 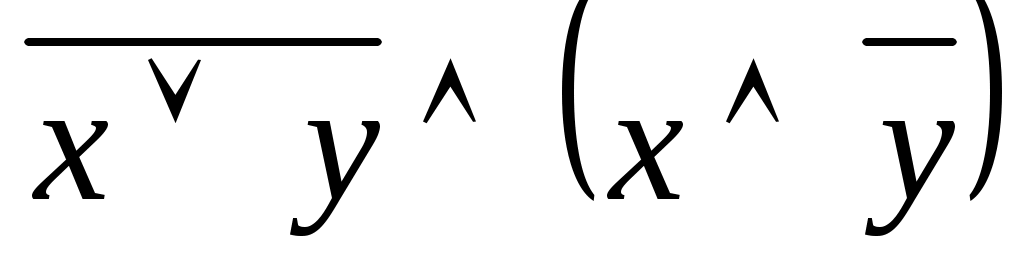 , , 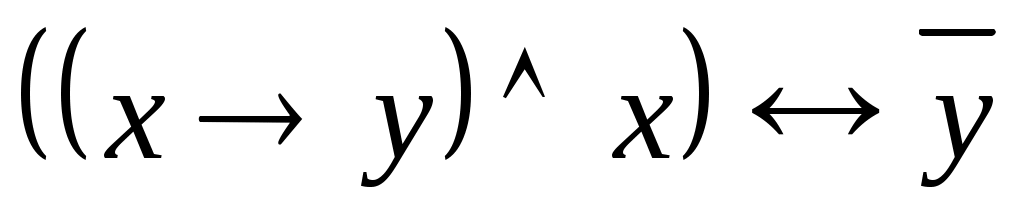 , ,  , , 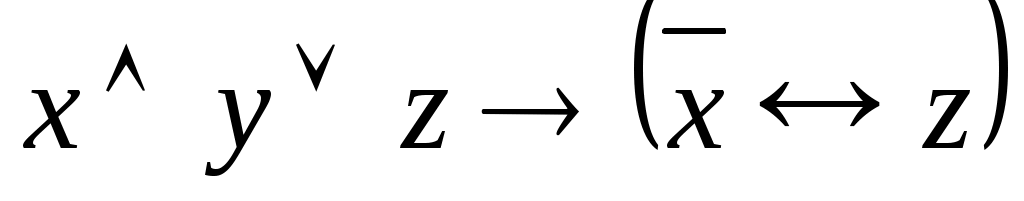 . .
|
2
|
ССА-22
|
Элементы высшей математики
|
Практическая работа по теме: Неопределенный интеграл и его свойства.
Задания смотри ниже
|
2
|
ССА-22
|
Дискретная
математика
|
Практическая работа по теме: Множества. Операции над множествами.
ВАРИАНТ 1 – Ермолаев, Ставицкий
1. Укажите все подмножества множества:
а) А={4};
б) В= {8,9};
в) С={d,u,k};
г) D=Ø;
д) четырехэлементные подмножества F={черный, синий, красный, желтый, коричневый}.
2. Найдите  С\D, D\C, если известно, что С={x С\D, D\C, если известно, что С={x R: -1 R: -1
D={ x R: -5≤x≤3}. R: -5≤x≤3}.
3. Найдите множества А и В, если 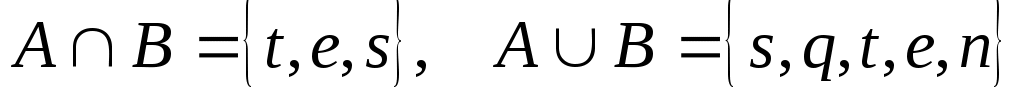 . .
4. В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и максим, и Земфиры?
5. В камеру заключен 31 заключенный, известно, что 20 заключенных отбывают наказание по ст. 105 УК РФ, по ст. 111 – 14 заключенных, по ст. 116 – 11 человек. Одновременно по двум статьям 105 и 111 осуждено 6 человек, по 105 и 116 – 5 человек, по 111 и 116 – 3 человека. Сколько человек в камере осуждено по трём статьям одновременно?
6. Известно, что в семьях, в которых содержат домашних животных, 50% кошек, 40% собак, 35% попугаев, причем собак и кошек содержат лишь 10% семей, собак и попугаев – 15%, кошек и попугаев – 10%. Сколько процентов семей содержат только одного животного?
7. Даны два множества А={-2,0,1,2,3,4} и В ={-1,0,1,2}. Найти декартовы произведения множеств: АхВ, ВхА, А2.
ВАРИАНТ 2 – Заболотный, Таран
1.Укажите все подмножества множества:
а) А={-5};
б) В= {3,-7};
в) С={g, f, a};
г) D=Ø;
д) четырехэлементные подмножества F={черный, белый, золотой, бирюзовый, оранжевый}.
2. Найдите  С\D, D\C, если известно, что С={x С\D, D\C, если известно, что С={x R: 0 R: 0
D={ x R: -6≤x≤2}. R: -6≤x≤2}.
3. Найдите множества А и В, если  . .
4. Из 17 человек в шахматы умеют играть 7 человек, в нарды – 11 человек, в шашки – 7 человек, причем в шашки и шахматы умеют играть 4 человека, в нарды и шахматы – 4 человека, в шашки и нарды – 5 человек. Сколько человек умеют играть во все игры?
5. В течение некоторого времени число дождливых дней было ровно 10, ветреных – 8, холодных – 6, дождливых и ветреных -5, дождливых и холодных – 4, ветреных и холодных – 3, и, наконец, дождливых, ветреных и холодных – 1. Сколько было всего дней с плохой погодой?
6. В библиотеку записаны 87 читателей. Известно, что 46 читателей периодически берут романы, 46 – научно-техническую литературу, 51- фантастику, причем читают и романы, и научно-техническую литературу 12 человек, романы и фантастику – 14, фантастику и научно-техническую литературу – 31 читатель. Сколько человек в библиотеке читает только романы?
7. Даны два множества А={1,2,3,4} и В ={5,6,7,8,9}. Найти декартовы произведения множеств: АхВ, ВхА, В2.
ВАРИАНТ 3 – Милютин, Юдин
1.Укажите все подмножества множества:
а) А={1};
б) В= {-3,12};
в) С={f, z, m };
г) D=Ø;
д) четырехэлементные подмножества F={зеленый, белый, голубой, фиолетовый, золотой}.
2. Найдите  С\D, D\C, если известно, что С={x С\D, D\C, если известно, что С={x R: -8 R: -8
D={ x R: -4≤x≤6}. R: -4≤x≤6}.
3. Найдите множества А и В, если 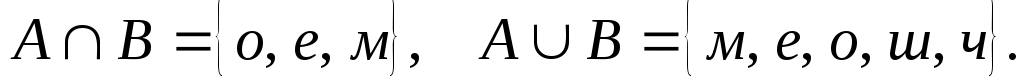
4. Из 26 зажиточных семей города N-ска у 20 как минимум по одной машине, у 8 семей имелся катер, и 6 семей - самолет. Известно, что 4 семьи одновременно владели машиной и катером, 3 – катером и самолетом и 3 семьи – машиной и самолетом. Сколько семей одновременно обладает машиной, катером и самолетом?
5. В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 – микроволновку и телевизор, 15 – холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
6. Из всего состава кафедры 95% преподавателей ведут занятия на радиотехническом факультете, 20% - на юридическом, 80% - на факультете заочного обучения. На двух факультетах: РТ и ЮФ ведут занятия 15 % преподавателей; ФЗО и РТ – 75%; ЮФ и ФЗО – 10%. На трёх факультетах работает 5% преподавателей. Известно также, что только на ФЗО никто не работает. Сколько процентов преподавателей кафедры работает только на радиотехническом факультете?
7. Даны два множества А={4,6,7,9,10} и В ={1,2,3}. Найти декартовы произведения
множеств: АхВ, ВхА, А2.
ВАРИАНТ 4 - Лизнев
1.Укажите все подмножества множества:
а) А={9};
б) В= {2,-5};
в) С={d,n,x};
г) D=Ø;
д) четырехэлементные подмножества F={красный, оранжевый, желтый, сиреневый, салатовый}.
2. Найдите  С\D, D\C, если известно, что С={x С\D, D\C, если известно, что С={x R: -4 R: -4
D={ x R: -9≤x≤2}. R: -9≤x≤2}.
3. Найдите множества А и В, если 
4. В группе 30 курсантов. У 17 из них имеются задолженности по математике, у 11 – по физике, у 13 – по информатике, причем задолженности по математике и физике имеют 4 курсанта, по математике и информатике – 5 курсантов, по физике и информатике – 6 курсантов. Из всей группы только два курсанта не имеют задолженностей по этим предметам. Сколько курсантов имеют задолженности по трём предметам?
5. В школе зимой работали 3 секции (лыжная, хоккейная, конькобежная). Всего в секциях занималось 38 учеников. В лыжной – 21 человек, среди которых трое ещё занимались коньками, шестеро – ещё в хоккейной секции, а один – сразу в трех секциях. В конькобежной секции было 13 человек, среди которых пятеро занимались сразу в двух секциях. Сколько человек занималось в хоккейной секции?
6. При наступлении холодов из 40 студентов 13 человек пришли в институт в шапках, 15 – в шарфах, 29 – в перчатках; причем одновременно надели шапки и перчатки 6 студентов, шарф и перчатки – 9 студентов, шарф и шапку – 4 студента, все три предмета одежды надели 2 студента. Сколько человек было одето только в один из предметов?
7. Даны два множества А={-1,0,4,6,8} и В ={8,5,9}. Найти декартовы произведения множеств: АхВ, ВхА, А2.
ВАРИАНТ 5 - Крымов
1.Укажите все подмножества множества:
а) А={25};
б) В= {-6,14};
в) С={e,s,h};
г) D=Ø;
д) четырехэлементные подмножества F={синий, голубой, красный, сиреневый, серый}.
2. Найдите  С\D, D\C, если известно, что С={x С\D, D\C, если известно, что С={x R: 0 R: 0
D={ x R: -3≤x≤3}. R: -3≤x≤3}.
3.Найдите множества А и В, если 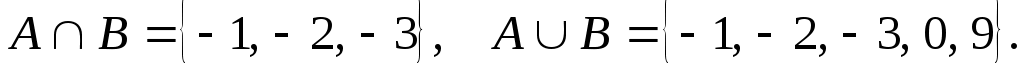
4. Из 25 человек студенческой группы по результатам психологического теста 12 человек оказались веселого характера, 16 – замкнутыми и 8 не показали себя ни веселыми, ни замкнутыми. Сколько человек оказались одновременно веселого, но замкнутого характера?
5. На контрольной работе было дано три задания. Правильно выполнили первое задание 18 студентов, второе задание – 9 студентов, третье задание – 13 студентов, причем правильно выполнивших первое и второе задания, оказались 3 студента, первое и третье – 7 студентов, второе и третье – 5 студентов. Все три задания правильно выполнили 2 студента. Сколько студентов неправильно выполнили все три задания, если в группе 32 студента?
6. В группе у 11 студентов имеются водительские права на категорию «А», у 11 студентов – на категорию «Б», у 11 – на категорию «С», у 2 студентов имеются права на все три категории. Категории «А» и «В» имеют 3 студента, «А» и «С» - 5 студентов, «В» и «С» - 4 студента. Сколько студентов в группе?
7. Даны два множества А={-1,0,3,4,2} и В ={-3,-2,-1,0}. Найти декартовы произведения этих множеств: АхВ, ВхА, А2.
ВАРИАНТ 6 - Михайлова
1.Укажите все подмножества множества:
а) А={8};
б) В= {-5,17};
в) С={t, q, y};
г) D=Ø;
д) четырехэлементные подмножества F={серый, черный, белый, бирюзовый, синий}.
2. Найдите  С\D, D\C, если известно, что С={x С\D, D\C, если известно, что С={x R: 3 R: 3
D={ x R: -1≤x≤4}. R: -1≤x≤4}.
3. Найдите множества А и В, если 
4. Некоторые ребята из нашего класса любят ходить в кино. Известно, что 12 ребят смотрели фильм «Ёлки», 9 человек – фильм «Неудержимый», из них 6 смотрели и «Ёлки», и «Неудержимый» . Сколько человек смотрели фильм «Неудержимый»?
5. В институте имеется 24 кафедры, в распоряжении которых находятся кабинеты и аудитории, расположенные на трёх этажах. Известно, что на первом этаже имеют кабинеты 7 кафедр, на втором – 8 кафедр, на третьем – 15 кафедр, причем на первом и втором этажах расположены кабинеты 2 кафедр, на первом и третьем – 3 кафедр, на втором и третьем – 3 кафедр. Сколько кафедр имеют кабинеты только на третьем этаже?
6. В спортивном лагере 100 человек, занимающихся плаванием, легкой атлетикой и лыжами. Из них 10 занимаются и плаванием, и легкой атлетикой, и лыжами, 18 – плаванием и легкой атлетикой, 15 – плаванием и лыжами, 21 – легкой атлетикой и лыжами. Число спортсменов, занимающихся плаванием, равно числу спортсменов, занимающихся легкой атлетикой, и равно числу спортсменов, занимающихся лыжами. Найти это число.
7. Даны два множества А={1,2,3} и В ={-2,0,4,6}. Найти декартовы произведения множеств: АхВ, ВхА, В2.
ВАРИАНТ 7 - Наборщиков
1.Укажите все подмножества множества:
а) А={7};
б) В= {-6,15};
в) С={h, w, v };
г) D=Ø;
д) четырехэлементные подмножества F={синий, фиолетовый, зеленый, золотой, коричневый}.
2. Найдите  С\D, D\C, если известно, что С={x С\D, D\C, если известно, что С={x R: -3 R: -3
D={ x R: -7≤x≤3}. R: -7≤x≤3}.
3. Найдите множества А и В, если 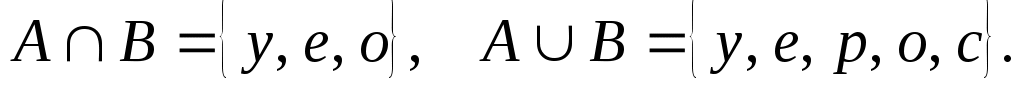
4. В группе 28 студентов, на первую пару пришли 9 студентов, на вторую – 14 студентов, на третью – 16 студентов; на первой и второй парах присутствовали 3 студента, на второй и третьей – 9 студентов, на первой и третьей – 3 студента, 2 студента не были ни на одной из пар. Сколько студентов присутствовали на трех занятиях?
5. В классе 20 детей. Из них 10 дополнительно занимаются в музыкальной школе, 6 –теннисом, 5 – китайским языком. Музыкальную школу и занятия по теннису посещают три ребёнка, музыкой и китайским языком занимаются трое, теннисом и китайским языком двое. Всеми тремя видами дополнительных занятий занимается один ребёнок. Сколько детей не занимается ни одним из перечисленных занятий?
6. Из 64 студентов на вопрос, занимаются ли они в свободное время спортом, утвердительно ответили 40 человек; на вопрос, любят ли они слушать музыку, 30 человек ответили утвердительно, причем 22 студента занимаются спортом и любят слушать музыку. Сколько человек не увлекается ни спортом, ни музыкой?
7. Даны два множества А={-2,0,1} и В ={4,6,8,9}. Найти декартовы произведения множеств: АхВ, ВхА, В2.
ВАРИАНТ 8 - Пузряков
1.Укажите все подмножества множества:
а) А={10};
б) В= {-4,11};
в) С={r, t, a};
г) D=Ø;
д) четырехэлементные подмножества F={сиреневый, салатовый, голубой, красный, желтый}.
2. Найдите  С\D, D\C, если известно, что С={x С\D, D\C, если известно, что С={x R: 2 R: 2
D={ x R: -3≤x≤5}. R: -3≤x≤5}.
3. Найдите множества А и В, если 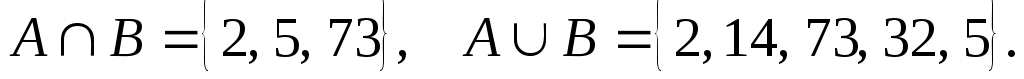
4. После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре – 11; в цирке -17; в кино, и в театре – 6; и в кино, и в цирке – 10; и в театре, и в цирке -4. Сколько человек побывали в театре, кино и цирке одновременно?
5. Группа научных работников состоит из 100 человек. Из них 70 человек владеют английским языком, 50 – немецким, 40 – французским, 30 – английским и немецким, 25 – английским и французским, 15 – французским и немецким. Хотя бы один язык знает каждый научный работник. Сколько человек владеют всеми тремя языками?
6. Из 220 школьников 163 играют в баскетбол, 175 – в футбол, 24 не играют в эти игры. Сколько школьников одновременно играют в баскетбол и футбол?
7. Даны два множества А={1,2,3} и В ={4,6,7,9,10}. Найти декартовы произведения
множеств: АхВ, ВхА, В2.
ВАРИАНТ 9 - Пярастари
1.Укажите все подмножества множества:
а) А={5};
б) В= {-3,-10};
в) С={w, q, r };
г) D=Ø;
д) четырехэлементные подмножества F={коричневый, кирпичный, красный, белый, оранжевый}.
2. Найдите  С\D, D\C, если известно, что С={x С\D, D\C, если известно, что С={x R: -1 R: -1
D={ x R: 0≤x≤6}. R: 0≤x≤6}.
3. Найдите множества А и В, если 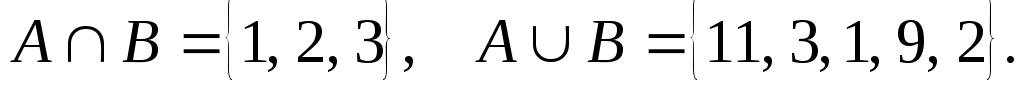
4. В классе 35 учеников. 24 из них играют в футбол, 18 – в волейбол, 12 – в баскетбол. 10 учеников одновременно играют в футбол и волейбол, 8 – в футбол и баскетбол, 5 – в волейбол и баскетбол. Сколько учеников играют и в футбол, и в волейбол, и в баскетбол одновременно.
5. В студенческой группе 25 человек. Чтобы получить допуск на экзамен по данному курсу необходимо защитить курсовую работу, выполнить лабораторную работу и сдать зачет. 15 студентов защитили курсовую работу, 20 выполнили лабораторную работу, 17 сдали зачет. Защитили курсовую работу и выполнили лабораторную работу 12 человек. Защитили курсовую работу и сдали зачет 13 человек. Выполнили лабораторную работу и сдали зачет 16 человек. Сколько студентов допущено к экзамену?
6. При обследовании рынка спроса инспектор указал в опросном листе следующие данные. Из 1000 опрошенных 811 покупают жевательную резинку "Дирол", 752 – "Орбит" , 418 – "Стиморол", 570 – "Дирол" и "Орбит", 356 – "Дирол" и "Стиморол", 348 – "Орбит" и "Стиморол", 297 – все виды жевательной резинки. Показать, что инспектор ошибся.
7. Даны два множества А={-6,3,5} и В ={1,4,5,-9 }. Найти декартовы произведения множеств: АхВ, ВхА, В2.
ВАРИАНТ 10 - Смоляков
1.Укажите все подмножества множества:
а) А={11};
б) В= {-2, -3};
в) С={I, j, t};
г) D=Ø;
д) четырехэлементные подмножества F={оливковый, оранжевый, лиловый, белый, синий}.
2. Найдите  С\D, D\C, если известно, что С={x С\D, D\C, если известно, что С={x R: 1 R: 1
D={ x R: -4≤x≤4}. R: -4≤x≤4}.
3.Найдите множества А и В, если 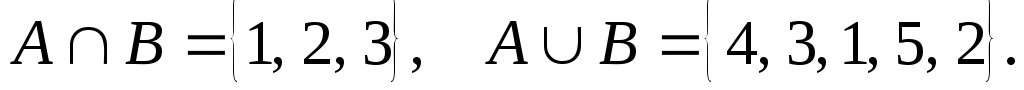
4.Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели фильм «Стиляги».
5. В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуются тремя видами транспорта?
6. Из 20 студентов группы 14 посещают дополнительные курсы английского языка, 11 – одновременно дополнительные курсы английского языка и информатики, 4 не посещают дополнительных курсов. Сколько студентов посещают дополнительные курсы информатики?
7. Даны два множества А={2,3,4,9} и В ={-8,-6,2}. Найти декартовы произведения множеств: АхВ, ВхА, А2.
|
2
|
ИСП-23
|
Дискретная математика с элементами математичес-
кой логики
|
Изучить лекцию и переписать в тетрадь.
Практическая работа: Основные законы алгебры логики. Упрощение логических выражений.
ВАРИАНТ 1 – Алхимов, Андреев, Вякин, Гордиенко, Некрылов
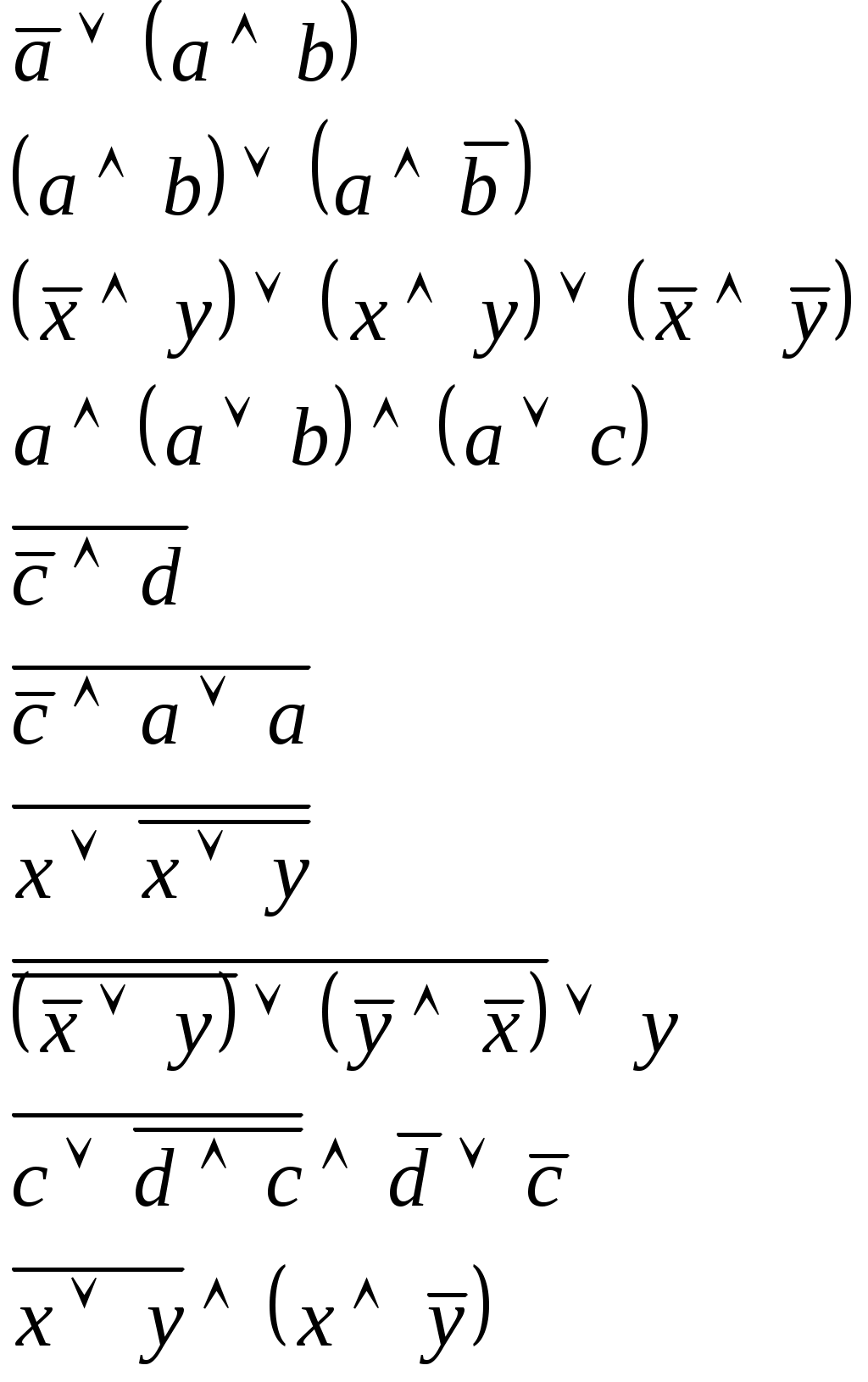
ВАРИАНТ 2 –Мещерина, Петров, Туркин, Хмелев
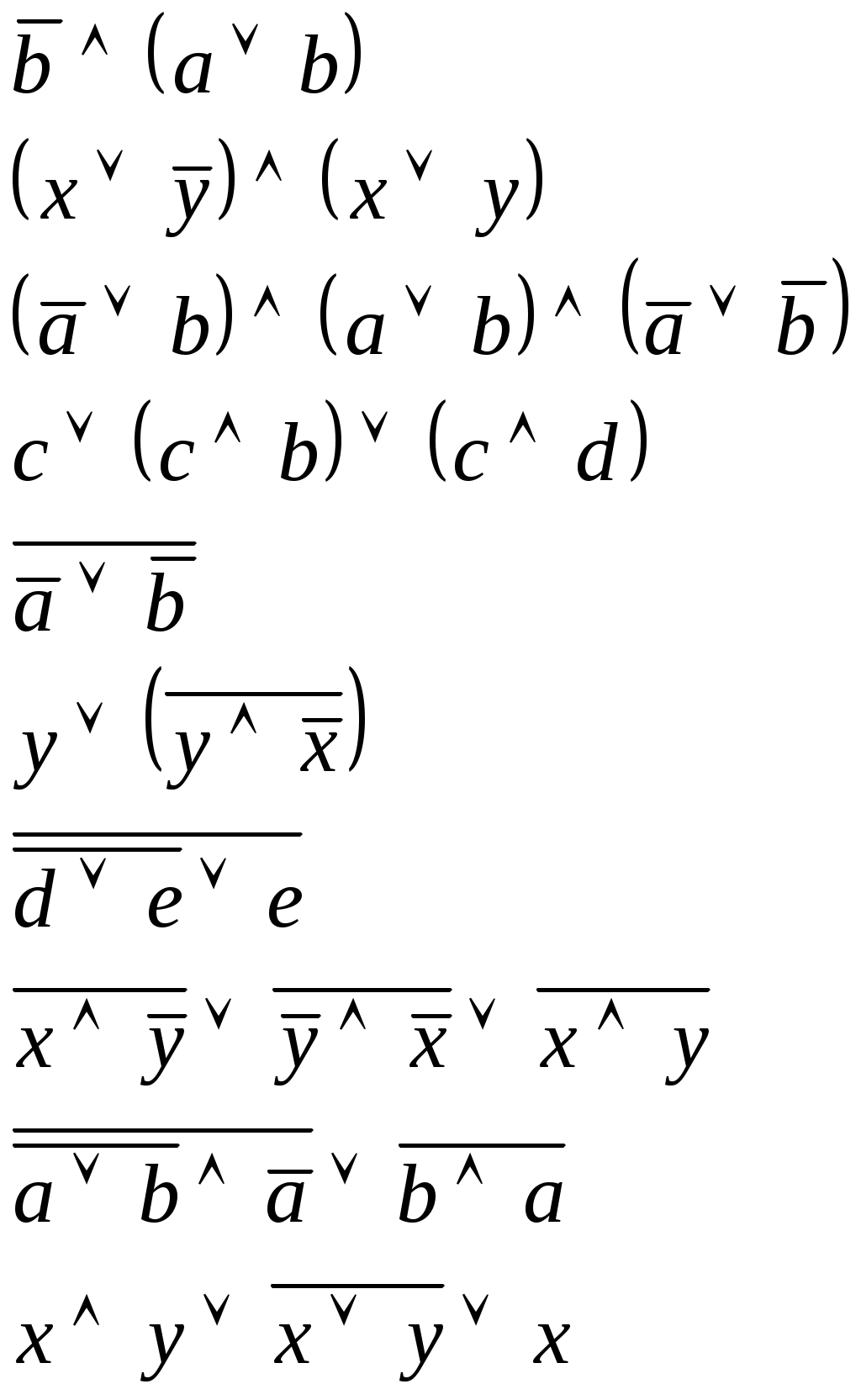
ВАРИАНТ 3 – Квитченко, Бородин, Рекун, Труевский, Тюленев
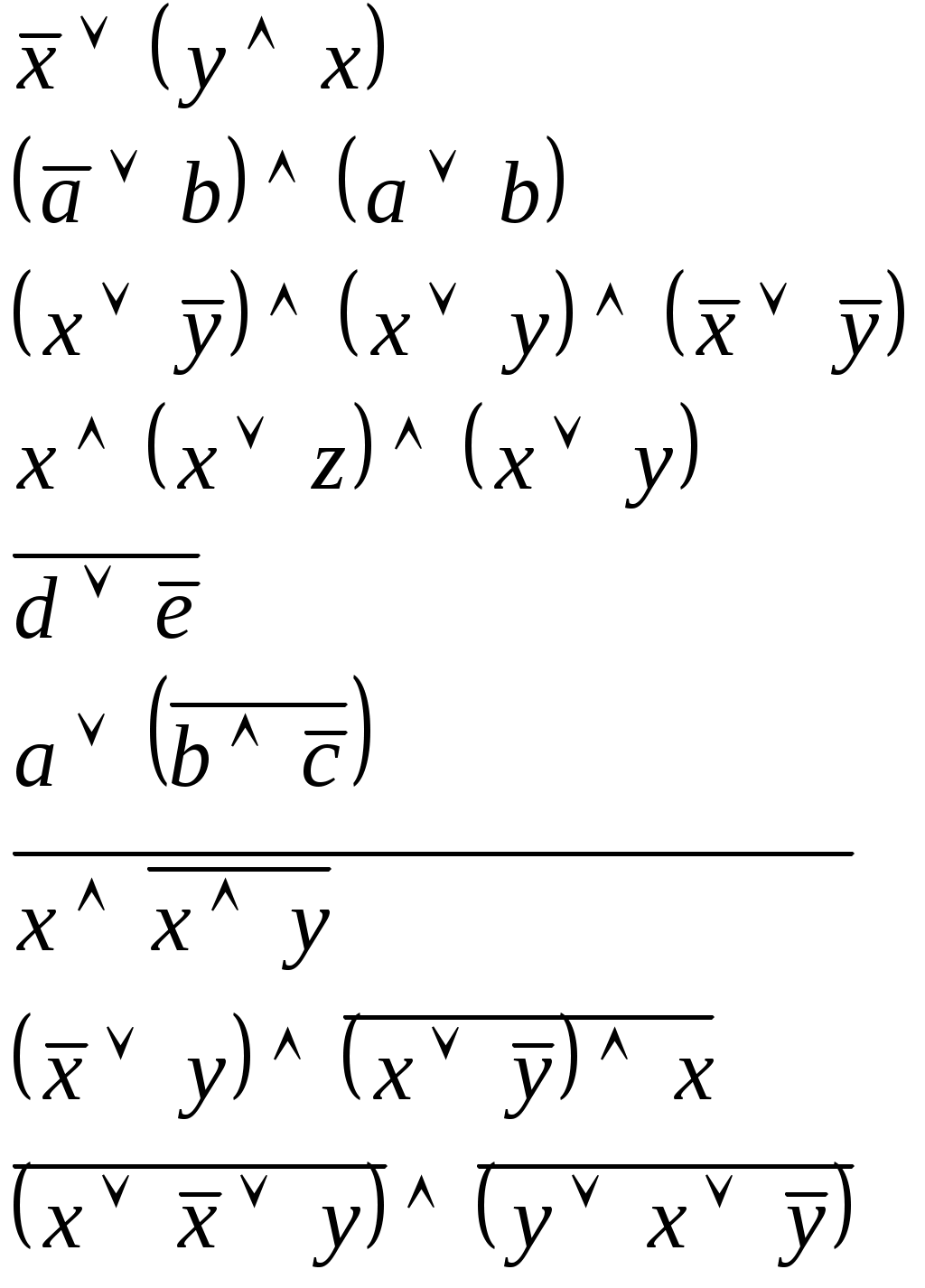
ВАРИАНТ 4 – Смирнов, Федоров, Егоров, Самсонов, Комов

Законы алгебры логики.
-
Закон
|
Для ИЛИ « » »
|
Для И « » »
|
Переместительный (коммутативный)
|

|
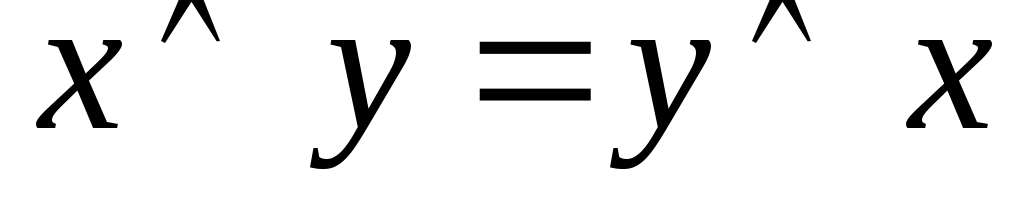
|
Сочетательный
(ассоциативный)
|

|

|
Распределительный
(дистрибутивный)
|

|

|
Закон де Моргана
|
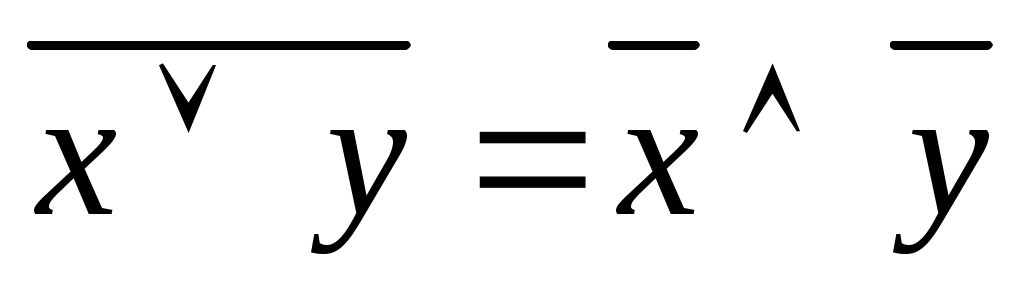
|

|
Идемпотенция
|
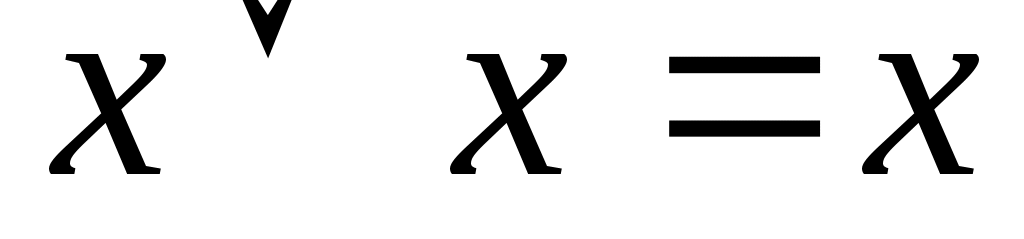
|

|
Закон поглощения
|

|
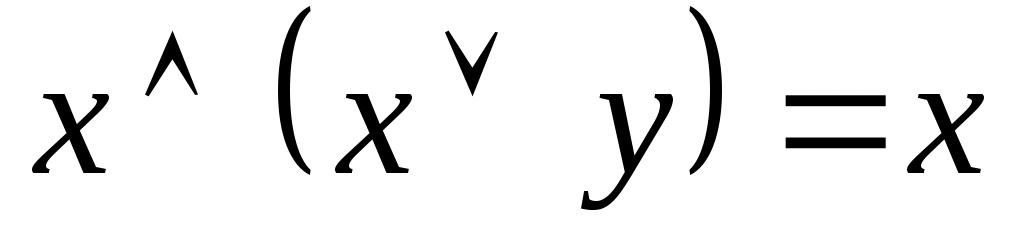
|
Закон склеивания
|
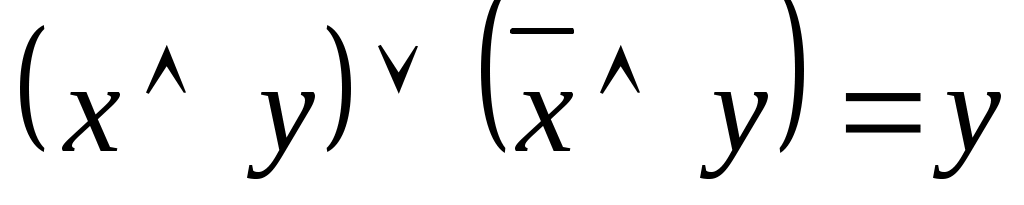
|
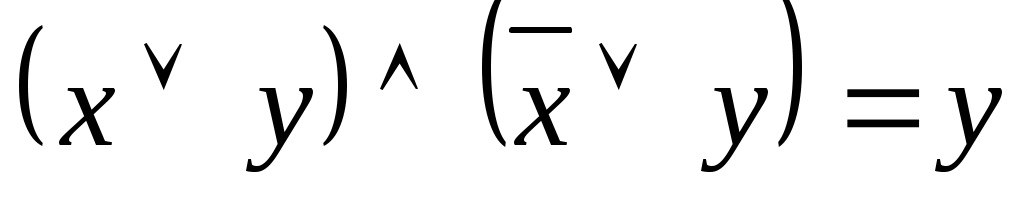
|
Операция переменной с её инверсией
|

|
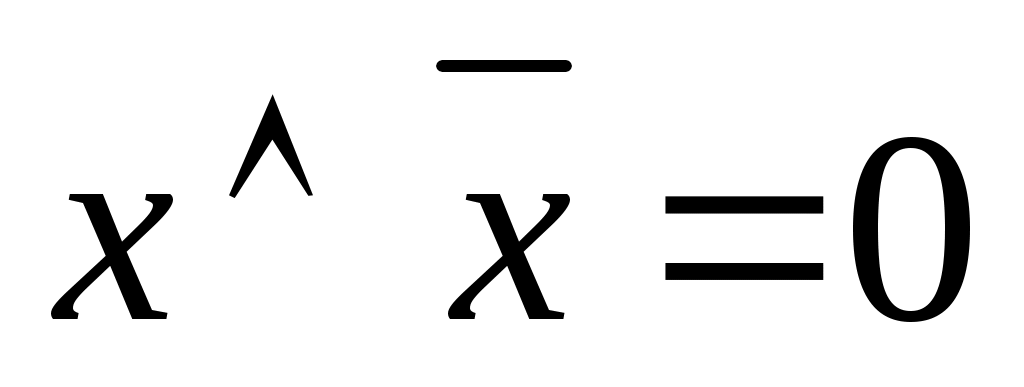
|
Операция с константами
|

|

|
Двойное отрицание
|
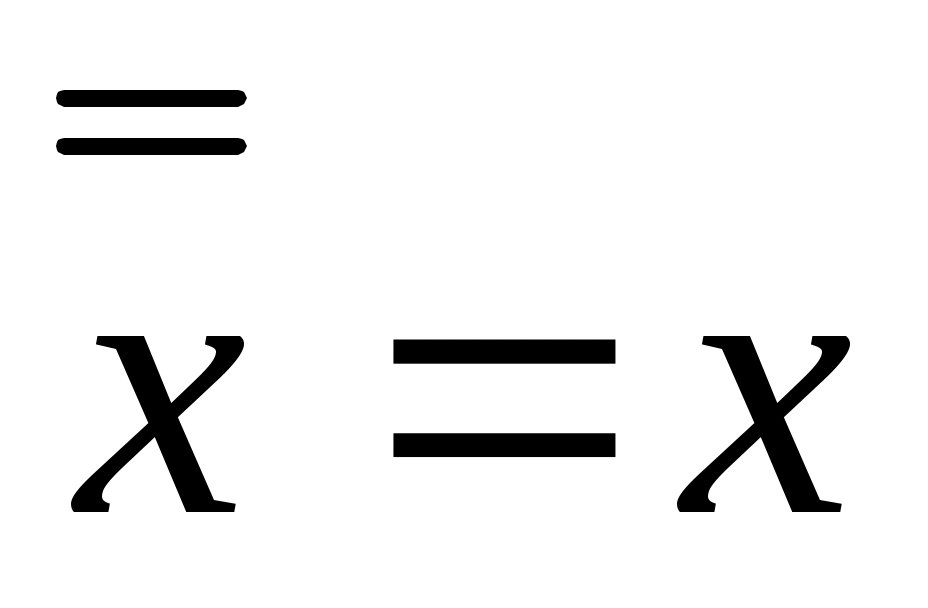
|
|
2
|
МТО-21
|
Математика
|
Практическая работа по теме: Неопределенный интеграл и его свойства.
Задания смотри ниже
|
-
ВАРИАНТ 1
Ермолаев, Юдин
Алимов, Алпатов
|
ВАРИАНТ 2
Заболотный, Таран
Жеглов, Седов
|
Найдите неопределённый интеграл:

|
Найдите неопределённый интеграл:

|
-
ВАРИАНТ 3
Крымов, Наборщиков
Янин, Косолапов
|
ВАРИАНТ 4
Лизнев
Курнин
|
Найдите неопределённый интеграл:
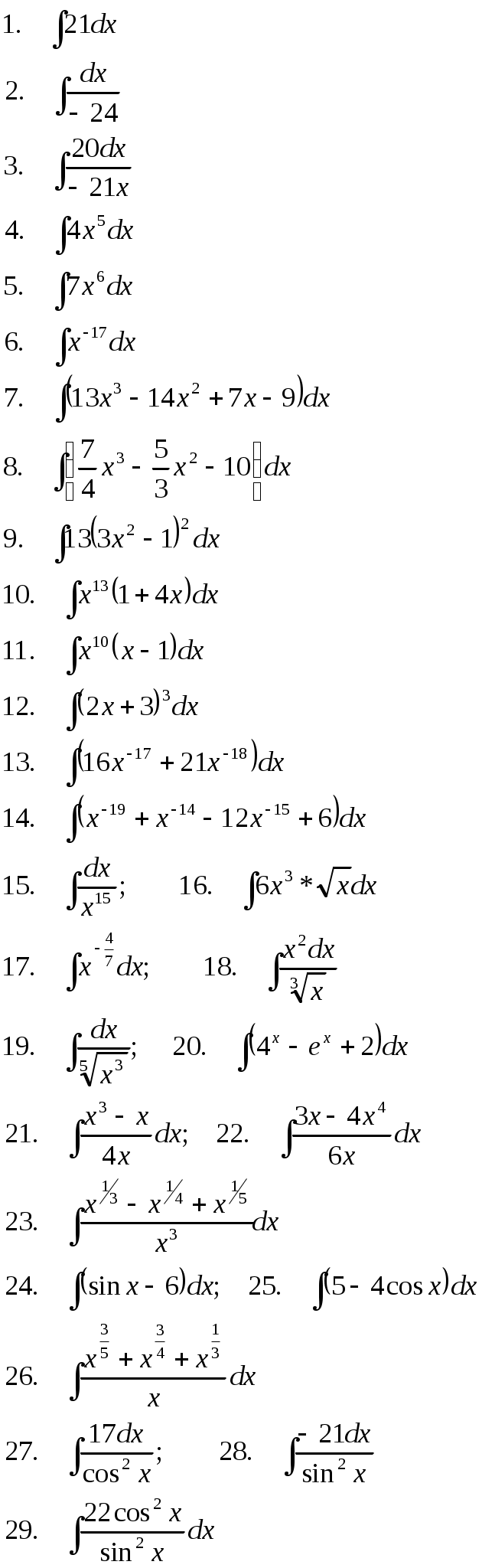
|
Найдите неопределённый интеграл:
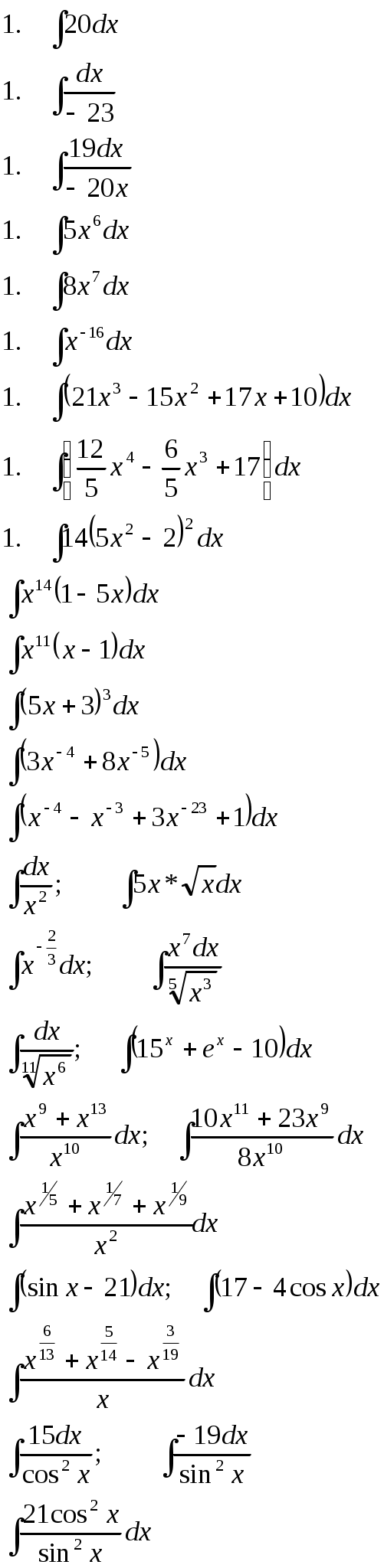
|
-
ВАРИАНТ 5
Милютин
Панин
|
ВАРИАНТ 6
Михайлова
Титов
|
Найдите неопределённый интеграл:
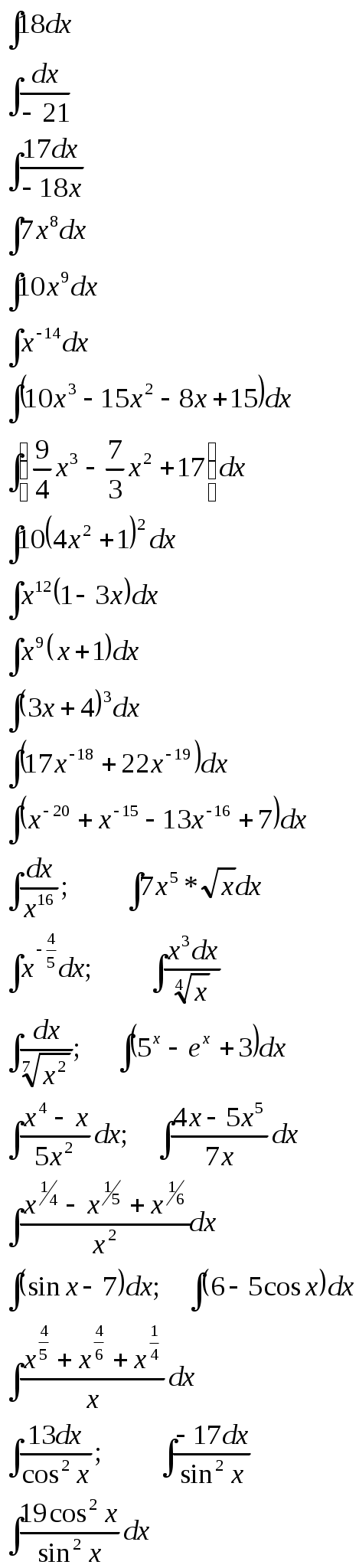
|
Найдите неопределённый интеграл:

|
-
ВАРИАНТ 7
Пузряков
Фролов
|
ВАРИАНТ 8
Пярастари
Харченко, Гурбанов
|
Найдите неопределённый интеграл:
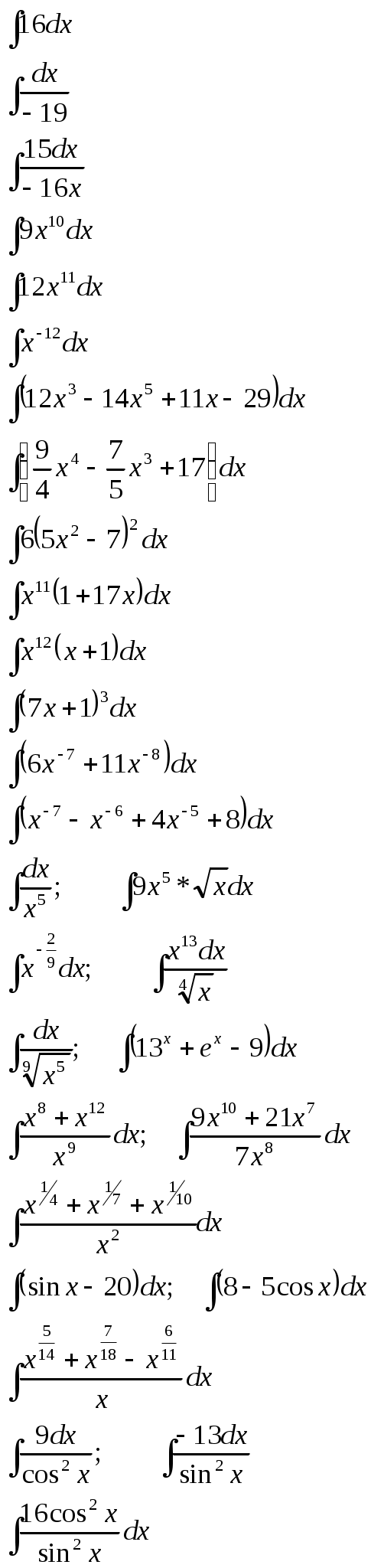
|
Найдите неопределённый интеграл:
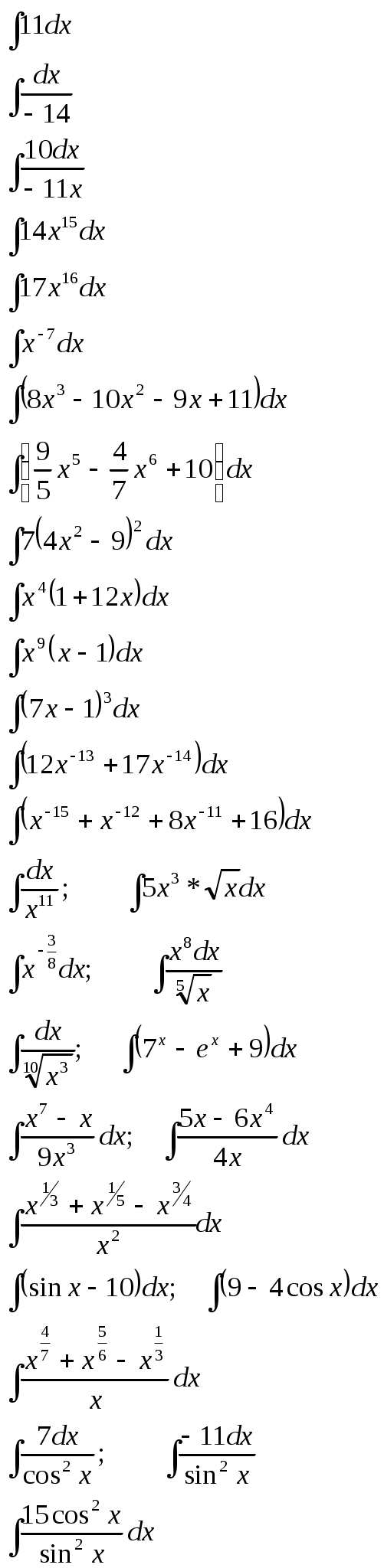
|
-
ВАРИАНТ 9
Смоляков
Юдин, Шабашов
|
ВАРИАНТ 10
Ставицкий
Куренков
|
Найдите неопределённый интеграл:
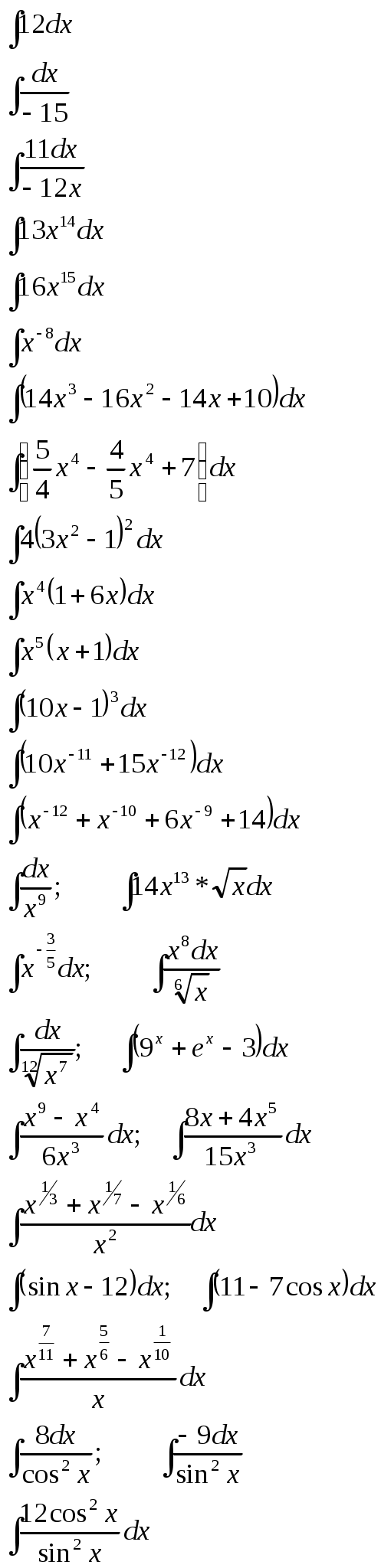
|
Найдите неопределённый интеграл:
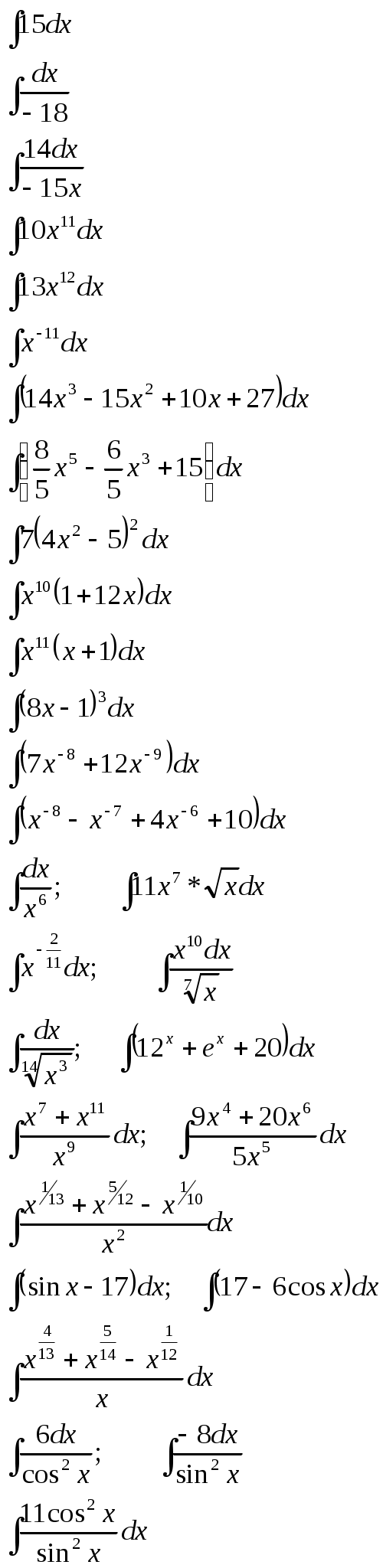
| |
|
|
 Скачать 416.5 Kb.
Скачать 416.5 Kb.