множества. 2. Множества.. Превзойти свою человеческую ограниченность и покорить Вселенную
 Скачать 56.01 Kb. Скачать 56.01 Kb.
|
|
Превзойти свою человеческую ограниченность и покорить Вселенную. Филдсовская премия. Множества.Эта глава посвящена множествам, что такое множество, какие действия можно выполнять над ними. К сожалению, нельзя дать строгого определения основному понятию теории – множества. Можно сказать, что множество — это «совокупность», «коллекция», «собрание», «группа» и т. д. Однако это не математические определения, а лишь синонимы могучего русского языка. Для определения любого понятия можно сказать, частным случаем какого более общего понятия оно является. К сожалению, для понятия множества так сделать не получится, так как более общего понятия чем множество, в математике нет. Что бы как-то определить понятие множество, мы его проиллюстрируем на примерах. Не редко мы говорим о вещах, объединённых одним признаком. Так можно сказать о множестве всех деревьев в лесу, о множестве всех соцветий на кусте сирени, о множестве рыб в океане, о множестве всех точек на плоскости и т. д. Элемент множества – это предметы составляющие данное множество. Для того чтобы указать, что множество 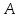 состоит из элементов состоит из элементов 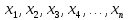 , обычно записывают в следующем виде: , обычно записывают в следующем виде: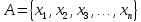 Фигурные скобки показывают, что элементы множества объединены в одно целое. Например, множество дней недели состоит из элементов {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}, множество месяцев — из элементов {январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь}, множество арифметических действий — из элементов {сложение, вычитание, умножение, деление}. Для того что бы указать принадлежность элемента x к множеству A используют знак 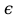 (принадлежащие), получается следующее: (принадлежащие), получается следующее: 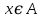 . Если элемент не принадлежит множеству, то используется знак не принадлежит ( . Если элемент не принадлежит множеству, то используется знак не принадлежит (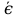 ). Например если ). Например если 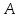 множество не четных натуральных чисел, то множество не четных натуральных чисел, то 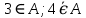 . Если . Если 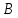 множество все дней недели, то множество все дней недели, то 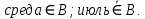 Теорию множеств основал Георг Кантор и подчеркнул, что «Множество есть многое, мыслимое нами как единое». Когда говорят о множествах, то объединяют некоторые предметы в одно целое, а именно в множество, элементами которого они являются. Чтобы понять, что такое множество, представьте непроницаемую прозрачную оболочку в виде мешка. Предположим, что внутри этой оболочки находятся все элементы множества 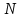 , и что больше, внутри оболочки предметов нет. Эта оболочка с предметами , и что больше, внутри оболочки предметов нет. Эта оболочка с предметами 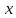 , находящимися внутри нее, и может служить образом множества , находящимися внутри нее, и может служить образом множества 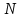 , составленного из элементов , составленного из элементов 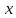 . Сама же оболочка, охватывающая все элементы, довольно хорошо изображает действие объединения элементов . Сама же оболочка, охватывающая все элементы, довольно хорошо изображает действие объединения элементов 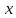 , в результате которого создается множество , в результате которого создается множество 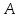 . .Конечное множество – это множество содержащее конечное число элементов. Например, множество деревьев в лесу конечно. Бесконечное множество – это множество содержащее бесконечное число элементов. Например, множество точек на окружности бесконечно. Пустое множество ( 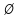 ) – это множество не содержащее ни одного элемента. Примерами пустого множества, являются количество петуний на луне, количество секунд в линейке, множество действительных корней квадратного уравнения ) – это множество не содержащее ни одного элемента. Примерами пустого множества, являются количество петуний на луне, количество секунд в линейке, множество действительных корней квадратного уравнения 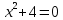 . .Состав множеств может быть совершенно различным — рыбы, дома, квадраты, чиса, точки и т. д. Собственно этим объясняется чрезвычайная распространенность теории множеств и ее применимость к различным областям (математике, биологии, информатике, механике, астрономии, физике, лингвистике и т. д.). Для математики важную роль играют множества, составленные из «математических» объектов — чисел, геометрических фигур, функций, алгебраических выражений и т. д. Школьная математика имеет дело с множествами постоянно, особенно часто встречаются числовые множества, то есть множества, составленные из чисел. Примерами таких множеств могут служить: множество всех натуральных чисел; множество всех целых чисел (положительных, отрицательных и нуля); множество всех рациональных чисел; множество всех действительных чисел; множество всех комплексных чисел. Область допустимых значений – это множество чисел, при которых, выражение, входящее в уравнение, имеет смысл. Множество решений – это множество всех возможных решений уравнения или неравенства. Подмножество – это множество которое рассматривается не самостоятельно, а как часть другого, более широкого множества. Говорят, что множество 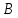 является подмножеством, множества является подмножеством, множества 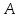 , если каждый элемент , если каждый элемент 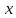 из из 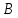 является и элементом множества является и элементом множества 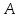 . В этом случае пишут B ⊂ A (A включает B). . В этом случае пишут B ⊂ A (A включает B).Например, множество всех волков является подмножеством в множестве всех хищных зверей, множество хищных зверей — подмножеством в множестве млекопитающих, а множество млекопитающих — подмножеством в множестве позвоночных. Если геометрическая фигура круг, является частью геометрической фигуры прямоугольник, то множество точек круга, есть подмножество множества точек прямоугольника. В геометрии часто приходится говорить о подмножестве множества геометрических фигур. Например 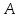 множество всех n-угольников, а множество множество всех n-угольников, а множество 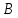 содержит все многоугольники с нечетным количеством вершин. Множество содержит все многоугольники с нечетным количеством вершин. Множество 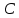 содержит все треугольники, а множество содержит все треугольники, а множество 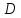 содержит все прямоугольные треугольники. В это списке фигура каждого типа является частным случаем более общего множества. содержит все прямоугольные треугольники. В это списке фигура каждого типа является частным случаем более общего множества. 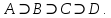 В следующем списке каждое следующее множество, является подмножеством предыдущего: множество всех комплексных чисел ( 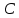 ); );множество всех действительных чисел ( 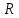 ); );множество всех рациональных чисел ( 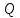 ); );множество всех целых чисел ( 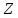 ); );множество всех натуральных чисел ( 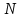 ). ).Чтобы выделить в множестве некоторое подмножество, добавляют к характеристическому признаку множества, дополнительное условие. Универсальное множество – это фиксированное множество, содержащее подмножества, с которыми имеют дело в том или ином рассуждении. Например, все числовые множества являются подмножествами множества действительных чисел, множество точек любой геометрической фигуры — подмножеством в множестве всех точек геометрического пространства, множество сторон плоского многоугольника — подмножеством в множестве всех отрезков на плоскости и т. д. Пересечение (произведение) множеств – это множество, состоящее из общих значений нескольких множеств. Пересечение множеств A, B обозначается AB или 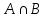 . . Произведение множеств AB. Например, врач ищет возбудитель инфекции, у одного больного есть свои микробы, у другого – другие, у третьего - третьи. Множества микробов у каждого больного различны, но хотя бы два или три будут совпадать, следовательно, хотя бы один из них может оказаться возбудителем данной болезни. После того как ссужен круг возбудителей болезни, можно провести дополнительные исследования и выявить точную угрозу, с последующим лечением. Метод геометрических мест – это один из основных метод для решения задач на построение. Сложение множеств – это множество, состоящее из элементов, которые входят хотя бы в одно из слагаемых множеств. Сумма множеств A, B обозначают A+B или 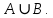    A∪B 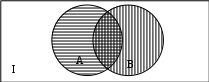 Сложение множеств A+B. С детства мы умеем складывать три яблока и две груши, по сути производя объединение двух множеств. Вообще, действие сложения натуральных чисел связано с подсчетом числа элементов объединения двух множеств. Есть небольшой нюанс при сложении множеств. Допустим у нас есть удобрение содержащее натрий, азот, марганец и кальций, а второе удобрение содержит азот, железо, калий и кальций. Если мы смешаем два удобрения, то получим смесь, содержащую шесть элементов: азот, марганец, натрий, кальций, калий, железо. Дело в том, что азот и кальций были в обоих удобрениях, то есть объединяемые множества элементов имели непустое пересечение. Поэтому будет правильно сказать, что сложение натуральных чисел связано с объединением непересекающихся множеств. Вместо вывода: теория множеств – это большой раздел математики, в котором изучаются общие свойства множеств — совокупностей элементов произвольной природы, обладающих каким-либо общим свойством. Мы рассмотрели лишь основы, которые пригодяться нам для дальнейшего понимания материала книги. Помимо сложения и умножения множеств их можно вычитать, отражать, декартово перемножать. Также у множеств есть характеристика, именуемая мощностью. Мы увидели, что множества встречаются нам в повседневной жизни постоянно, хотя мы их не всегда замечаем. Если вы хотите узнать о теории множеств больше, то советую прочитать следующую литературу: Виленкин Н.Я. Рассказы о множествах - 3. изд. МЦНМО, 2004 150с. Ануфриенко С.А. Введение в теорию множеств и комбинаторику: Учеб. пособие. Екатеринбург: УрГУ, 1998 62с. Белова, Л. Ю. Элементы теории множеств и математической логики. Теория и задачи: учебное пособие /Л. Ю. Белова, Б43 Ю. А. Белов; Яросл. гос. ун-т им. П. Г. Демидова. – Ярославль: ЯрГУ, 2012 – 204 с. Натуральные числа. Простые и составные числа. Делитель и кратное. Наибольший общий делитель. Наименьшее общее кратное. Признаки делимости на 2,3, 4, 5, 9, 10, 25. Множества целых, рациональных и действительных чисел. Координатная прямая. Модуль (абсолютная величина) действительного числа и его геометрический смысл. Степени и корни с натуральным показателем. Арифметический корень. Степени с нулевым, целым и рациональным показателями. Пропорция. Основное свойство пропорции. Проценты. Числовые выражения. Выражения с переменными. Тождественно равные выражения. Формулы сокращенного умножения. Тождественные преобразования алгебраических выражений, содержащих радикалы и модули. Разложение многочленов на множители. Алгебраические дроби. |
