Реферат. реферат приближенные вычb готовоc. Приближенные вычисления
 Скачать 32.38 Kb. Скачать 32.38 Kb.
|
|
Иссык-Кульский государственный университет Имени Касыма Тыныстанова Факультет русской филологии и иностранных языков РЕФЕРАТ на тему «Приближенные вычисления» Выполнила: студентка 1 курса группы Р-11 Коваленко. Я. Ю Проверила: Кулубекова . М .Т Каракол 2020 Содержание Введение…………………………………………………………………………...3 1.Приближенные вычисления…………………………………………………....4 2.Погрешности…………………………………………………………………….4 3.Округление………………………………………………………………………6 4.Действия над приближенными числами………………………………………7 Заключение…………………………………………………………………….….9 Литература……………………………………………………………………….10 Введение Быстрый расчет позволяет оценить без продолжительного изучения, примерное значение или вероятность. Далее мы уже можем, повышая точность и собирая факты, производить все более и более точные расчеты до тех пор, пока приближение не окажется настолько малым, что нас удовлетворит. Бывают случаи на практике , когда решая расчётную задачу, получает ответ, немного отличающийся от ответа, данного в задачнике, или ,например, у группы учащихся ответы различаются между собой. Незначительно, на десятые или даже сотые. Тем не менее возникает вопрос: какой ответ правильный при условии, что решение задачи верное? Однозначно можно утверждать, что суть этой проблемы заключена в способах вычислений, производимых учащимися. Точнее, в неправильных приближённых вычислениях. В математике есть целые разделы, где изложены правила приближённых вычислений, приведены доказательства теорем, следствия и т. п 1.Приближенные вычисления Вычисления, в которых данные и результат (или по крайней мере только результат) являются числами, лишь приближённо представляющими истинные значения соответствующих величин. Приближенные вычисления возникают в связи с численным решением задач и обусловлены неточностями, которые присущи формулировке задачи и способам её решения. Общие правила и теорию методов приближенных вычислений принято называть численными методами . Выполняя вычисления, всегда необходимо помнить о той точности, которую нужно или которую можно получить. Недопустимо вести вычисления с большой точностью, если данные задачи не допускают или не требуют этого (например, семизначная таблица логарифмов при вычислениях с числами, имеющими 5 верных значащих цифр - избыточна). Твёрдое знакомство с правилами приближенных вычислений необходимо каждому, кому приходится вычислять. . 2.Погрешности Разница между точным числом x и его приближенным значением a называется погрешностью данного приближенного числа. Если известно, что | x - a | < ∆a, то величина ∆a называется предельной абсолютной погрешностью приближенной величины a. Отношение ∆a / a = a называется предельной относительной погрешность последнюю часто выражают в процентах. Пример: 3,14 является приближенным значением числа , погрешность его равна 0,00159..., предельную абсолютную погрешность можно считать равной 0,0016, а предельную относительную погрешность v равной 0.0016/3.14 = 0,00051 = 0,051%. Для краткости обычно слово предельная опускается. Если абсолютная погрешность величины a не превышает одной единицы разряда последней цифры числа a, то говорят, что у числа все знаки верные. Приближенные числа следует записывать, сохраняя только верные знаки. Если, например, абсолютная погрешность числа 52400 равна 100, то это число должно быть записано, например, в виде 524 .102 или 0,524 .105. Оценить погрешность приближенного числа можно, указав, сколько верных значащих цифр оно содержит. При подсчете значащих цифр не считаются нули с левой стороны числа. Примеры:
Если число a имеет n верных значащих цифр, то его относительная погрешность , a 1/(z*dn-1), где z - первая значащая цифра числa a; d - основание системы счисления. У числа a с относительной погрешностью a верны n значащих цифр, где n - наибольшее целое число, удовлетворяющее неравенству 1+Z)a dl-n. Пример: Если число a = 47,542 получено в результате действий над приближенными числами и известно, что a = 0,1%, то a имеет 3 верных знака, так как (4+1)0,001 10v2. 3.Округление Если приближенное число содержит лишние (или неверные) знаки, то его следует округлить. При округлении сохраняются только верные знаки; лишние знаки отбрасываются, причем если первая отбрасываемая цифра больше или равна d/2, то последняя сохраняемая цифра увеличивается на единицу. При округлении возникает дополнительная погрешность, не превышающая половины единицы разряда последней значащей цифры округленного числа. Поэтому, чтобы после округления все знаки были верны, погрешность до округления должна быть не больше половины единицы того разряда, до которого предполагают делать округление. Правила округления Округлением десятичной дроби называютотбрасывание цифр этой дроби, следующих за некоторым разрядом. Округлением целого числа называют замену нулями цифр этого числа, следующих за некоторым разрядом -Если первая отбрасываемая цифра менше 5, то последняя сохраняемая цифра не изменяется. -Если первая отбрасываемая цифра больше 5, то последняя сохраняемая цифра увеличивается на единицу. -Если отбрасывается только цифра 5, то последняя сохраняемая цифра не изменяется, если она чётная, и увеличивается на единицу, если она нечётная. -Если отбрасывают цифру больше 5, а последняя сохраняемая цифра 9, то её заменяют нулём, а предпоследнюю цифру увеличивают на единицу. Если же несколько подряд сохраняемых цифр равны 9, то их заменяют нулями, а первая сохраняемая цифра, отличная от9(увеличивается на единиц). В итоговой записи сохраняются все десятичные знаки. Нельзя отбрасывать десятичные знаки, равные нулю. . 4.Действия над приближенными числами Результат действий над приближёнными числами представляет собой также приближённое число. Погрешность результата может быть выражена через погрешности первоначальных данных при помощи следующих теорем: 1.Предельная абсолютная погрешность алгебраической суммы равна сумме предельных абсолютных погрешностей слагаемых. 2.Относительная погрешность суммы заключена между наибольшей и наименьшей из относительных погрешностей слагаемых. 3.Относительная погрешность произведения или частного равна сумме относительных погрешностей сомножителей или, соответственно, делимого и делителя. 4.Относительная погрешность n-ой степени приближенного числа в n раз больше относительной погрешности основания (как у целых, так и для дробных n). Пользуясь этими теоремами, можно определить погрешность результата любой комбинации арифметических действий над приближенными числами. Примеры: V = r2h Dv = Vd v = V(2d r+d n) 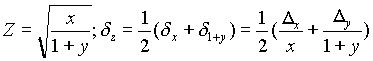 Предельная абсолютная погрешность заведомо превосходит абсолютную величину истинной погрешности, поскольку предельное значение вычисляется в предположения, что различные погрешности усиливают друг друга; практически это бывает редко. При массовых вычислениях, когда не учитывают погрешность каждого отдельного результата, пользуются следующими правилами подсчета цифр. При соблюдении этих правил можно считать, что в среднем полученные результаты будут иметь все знаки верными, хотя в отдельных случаях возможна ошибка в несколько единиц последнего знака. 1.При сложении и вычитании приближённых чисел в результате следует сохранять столько десятичных знаков, сколько их в приближённом данном с наименьшим числом десятичных знаков. 2.При умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет приближённое данное с наименьшим числом значащих цифр. 3.При возведении в квадрат или куб в результате следует сохранять столько значащих цифр, сколько их имеет возводимое в степень приближённое число ( последняя цифра квадрата и особенно куба при этом менее надежна, чем последняя цифра основания ). 4.При увеличении квадратного и кубического корней в результате следует брать столько значащих цифр, сколько их имеет приближённое значение подкоренного числа (последняя цифра квадратного и особенно кубического корня при этом более надёжна, чем последняя цифра подкоренного числа). 5.Во всех промежуточных результатах следует сохранять одной цифрой более, чем рекомендуют предыдущие правила. В окончательном результате эта запасная цифра отбрасывается. 6.Если некоторые данные имеют больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при умножении, делении, возведении в степень, извлечении корня), чем другие, то их предварительно следует округлить, сохраняя лишь одну лишнюю цифру. Если данные можно брать с произвольной точностью, то для получения результата с K цифрами данные следует брать с таким числом цифр, какое даёт согласно правилам 1-4(К+1) цифру в результате. Заключение Числа, с которыми мы имеем дело в жизни, бывают двух типов. Одни в точности дают истинную величину, другие — только приблизительно. Первые называют точными, вторые -приближенными. Часто мы сознательно берем приближенное число вместо точного, так как последнее нам не требуется. Во многих же случаях точное число невозможно найти по сути. Поэтому есть различные методы(правила) для работы с приближенными вычислениями. Список литературы 1.Дадаян А.А.Математика.-М.,2010 2. https://dic.academic.ru/dic.nsf/bse/ 3. https://ibrain.kz/matematika/priblizhennye-vychisleniya 4.Баврин И.И.Высшая математика.—М.,2002 . |
