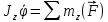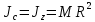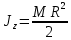Приложение общих теорем к динамике твердого тела
 Скачать 40.6 Kb. Скачать 40.6 Kb.
|
Практическое/семинарское занятие №14Тема: ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА Цель занятия: Приобретение навыков в применении теоремы об изменении кинетического момента точки и системы; вычисление кинетического момента вращающихся вокруг неподвижной оси тел. Пользоваться этой теоремой для изучения вращательного движения тел или для изучения движения систем, исключающих вращающиеся и поступательно движущиеся тела. Задания аудиторное, домашнее: 17.1-17.10; 18.1-18.7 Кинетический момент твердого тела, вращающегося вокруг неподвижной оси Oz равен 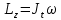 , где , где 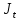 – момент инерции тела относительно оси вращения. – момент инерции тела относительно оси вращения.Теорема: Произведение момента инерции тела на его угловое ускорение равно сумме моментов всех сил приложенных к нему, относительно оси вращения
1. Моменты инерции некоторых тел Момент инерции относительно точки или оси характеризует распределение массы тела соответственно относительно точки или оси и представляет собой меру его инертности во вращательном движении. Момент инерции тела относительно точки О называется полярным моментом инерции; относительно осей Ox, Oy, Oz называются осевыми моментами инерции, причем:
1. Момент инерции стержня длиной lи массой М относительно центра масс C равен
2. Момент инерции тонкого кольца радиуса R и массы М относительно центра масс С равен
3. Момент инерции сплошного диска радиуса R массы М относительно центра масс С равен
4. Момент инерции круглого цилиндра R массы М относительно его оси равен
Пример 1: Упругую проволоку, на которой подвешен однородный шар с радиусом r и массой m, закручивают на угол 0, а затем предоставляют ей свободно раскручиваться. Момент, необходимый для закручивания проволоки на один радиан, равен C. Определить движение, пренебрегая сопротивлением воздуха и считая момент силы упругости закрученной проволоки пропорциональным углу кручения . Решение: Направим ось z по оси вращения твёрдого тела. На систему действуют: сила тяжести шара – 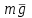 и сила упругости пружины, момент которой равен Мупр = – С. Выберем направление отсчёта угла по часовой стрелке, если смотреть с конца оси z, тогда Мупр – против часовой стрелки (отрицателен), т.к. противоположен положительному направлению. и сила упругости пружины, момент которой равен Мупр = – С. Выберем направление отсчёта угла по часовой стрелке, если смотреть с конца оси z, тогда Мупр – против часовой стрелки (отрицателен), т.к. противоположен положительному направлению.Запишем дифференциальное уравнение вращения твёрдого тела вокруг неподвижной оси: 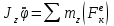 . .Jz – момент инерции шара известен и равен 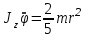 . .Момент силы тяжести относительно оси z равен 0. Следовательно, 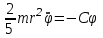 или или  , т.е. , т.е.  , где , где 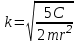 Это однородное дифференциальное уравнение. Решение его известно: 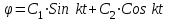 , , 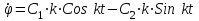 . .Определим произвольные постоянные: при t = 0, = 0 = 0,  = 0, С1 = 0, С2 = 0. = 0, С1 = 0, С2 = 0.Таким образом уравнением вращения является: 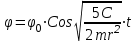 . .Ответ: 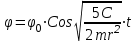 . . Примечание: Следует обратить внимание на то, что подобно теоремам о движении центра масс, об изменении главного вектора количеств движения системы материальных точек, в формулировку данной теоремы также не входят внутренние силы системы, определение которых обычно связано со значительными трудностями. Вопросы для контроля: Что называется кинетическим моментом механической системы относительно центра и оси? 1.1 Кинетическим моментом (моментом импульса) механической системы называют величину, равную сумме кинетических моментов (моментов импульса) всех тел, входящих в систему относительно центра приведения. ... - моменты импульса системы и главные моменты внешних сил относительно соответствующих осей координат. Как формулируется теорема об изменении кинетического момента системы относительно центра и оси? 2.2 Теорема формулируется так: производная по времени от кинетического момента механической системы (относительно данного неподвижного центра, данной неподвижной оси) равна главному моменту всех внешних сил системы (относительно того же центра, той же оси). Сформулировать закон сохранения кинетического момента системы. 1.1 Закон сохранения кинетического момента гласит: Если сумма моментов всех внешних сил, действующих на систему, относительно какой-либо оси равна нулю, то кинетический момент (момент импульса) системы относительно этой оси есть величина постоянная. Как определяется кинетический момент твёрдого тела, вращающегося вокруг неподвижной оси? 2.2 Кинетический момент, векторная динамич. мера механич. движения. К. м. GG материальной точки относительно неподвижной системы координат с началом в точке OO равен G=r×mvG=r×mv, где mm – масса точки, rr – её радиус-вектор, vv – скорость. К. м. материальной точки называется также моментом импульса или моментом количества движения. К. м. системы материальных точек равен геометрич. сумме К. м. всех точек системы. Что называется количеством движения механической системы? 3.3 Количеством движения (импульсом) механической системы называют величину, равную сумме количеств движения (импульсов) всех тел, входящих в систему. Импульс внешних сил, действующих на тела системы, — это сумма импульсов всех внешних сил, действующих на тела системы. Как формулируется теорема об изменении количества движения системы в дифференциальной и конечной формах? 4.4 Теорема об изменении количества движения системы утверждает: Изменение количества движения системы за некоторый промежуток времени равно импульсу внешних сил, действующих на систему, за тот же промежуток времени. Сформулируйте закон сохранения количества движения. 5.5 Закон сохранения импульса (закон сохранения количества движения) — закон, утверждающий, что сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю Могут ли внутренние силы изменить количество движения системы? 6.6 Эти результаты и выражают закон сохранения количества движения системы: при любом характере взаимодействия тел, образующих замкнутую систему, вектор полного импульса этой системы все время остается постоянным. Из них следует, что внутренние силы изменить суммарное количество движения системы не могут |