Применение численных методов в задачах программирования. Применение численных методов в задачах программирования
 Скачать 32.91 Kb. Скачать 32.91 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра радиотехнических систем (РТС) КУРСОВОЙ ПРОЕКТ по дисциплине «Информационные технологии» на тему «Применение численных методов в задачах программирования» Студент гр. - ________ - ________ Руководитель Ст.преподаватель каф. РТС ________ ________ Б.Ф. Ноздреватых ________ Томск 2022 ТЗ 1. Тема: Применение численных методов в задачах программирования. 2. Срок сдачи студентом законченной работы «16» мая 2022 г. 3. Требования: Пояснительная записка должна содержать теоретические основы используемых методов; Программа должна быть написана на языке Python и иметь графический интерфейс; Работоспособность программы должна быть протестирована на тестовых примерах, которые студент придумывает самостоятельно; Текст пояснительной записки должен содержать листинг программы с подробными комментариями; Проверка правильности программно-выполняемых расчётов должны быть подтверждена в математических пакетах Matlab и MathCAD; Оформление должно соответствовать ОС ТУСУР 01-2021. 4. Перечень подлежащих разработке вопросов: Решить нелинейное уравнение (вид определяет студент самостоятельно), методом половинного деления и методом хорд. Предоставить пользователю возможность вводить значения коэффициентов уравнения и выбор метода для расчёта. Результат выполнения задания предоставить в виде приложения под операционную систему Windows с графическим интерфейсом Оглавление Оглавление 3 Введение 4 1.ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 4 2.ПРАКТИЧЕСКАЯ ЧАСТЬ 6 Заключение 8 Приложение А 8 Введение Цель данного курсового проекта: написание программы с графическим интерфейсом для расчета нелинейных уравнений по методу хорд и половинного деления. Область исследования данного объекта: информационные технологии, математика. В этой курсовой работе рассказано о применение численных методов в задачах программирования. А именно о методе хорд и методе половинного деления, объясняется, что это за методы, по какому принципу они находят корни уравнений и их программная реализация. Так же важной деталью этого курсового проекта является создание графического интерфейса, для программы реализующей метод хорд и метод половинного деления. 1.ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 1.1 Метод хорд Метод хорд (метод также известен как Метод секущих) один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения. Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность. В отличие от метода половинного деления, метод хорд предлагает, что деление рассматриваемого интервала будет выполняться не в его середине, а в точке пересечения хорды с осью абсцисс (ось - Х). Следует отметить, что под хордой понимается отрезок, который проведен через точки рассматриваемой функции по концам рассматриваемого интервала. Рассматриваемый метод обеспечивает более быстрое нахождение корня, чем метод половинного деления, при условии задания одинакового рассматриваемого интервала. Метод хорд является итерационным алгоритмом, таким образом решение уравнения заключается в многократном повторении этого алгоритма. Полученное в результате вычислений решение является приближенным, но его точность можно сделать такой, какой требуется, задав нужное значение погрешности ε. В начале вычислений методом хорд требуется указать границы области поиска корня; в общем случае эта граница может быть произвольной. Итерационная формула для вычислений методом хорд следующая: 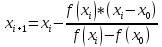 (1.1) (1.1)где, 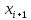 – приблизительное значение корня – приблизительное значение корня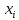 – предыдущее приблизительное значение корня – предыдущее приблизительное значение корня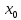 – начальное значение x – начальное значение x1.2 Метод половинного деления Метод половинного деления позволяет исключать в точности половину интервала на каждой итерации. При использовании метода считается, что функция непрерывна и имеет на концах интервала разный знак. После вычисления значения функции в середине интервала одна часть интервала отбрасывается так, чтобы функция имела разный знак на концах оставшейся части. Итерации метода деления пополам прекращаются, если интервал становится достаточно малым. 2.ПРАКТИЧЕСКАЯ ЧАСТЬ В практической части продемонстрированы навыки программирования и использования библиотек Python. Я использовал три библиотеки Math, PySide2 и PyInstaller. 2.1 Программная реализация метода хорд Программная реализация метода хорд на языке Python представлена ниже. def method_chord3(x_prev, x_curr, e): # параметры функции это левая граница, правая границы и погрешность while math.fabs(x_curr - x_prev) > e: x_prev = x_curr - (x_curr - x_prev) * f(x_curr) / (f(x_curr) - f(x_prev)) x_curr = x_prev - (x_prev - x_curr) * f(x_prev) / (f(x_prev) – f (x_curr)) return x_curr 2.2 Программная реализация метода половинного деления Программная реализация метода половинного деления на языке Python представлена ниже. def fun_findkoren(a,b): # Начальные параметры функции это правая и левая границы k = 0 f_a = f(a) f_b = f(b) while b-a > sigma and k < max_step: xm = a/2+b/2 f_xm = f(xm) if (f_a*f_xm <=0): b=xm f_b=f_xm else: a = xm f_a=f_xm return (a+b)/2 2.3 Проверка в Matlab и Mathcad Заключение В практической части показана программная реализация для метода хорд и метода половинного деления. Через эту программу пользователь может считать не линейные уравнения, подставляя свои коэффициенты, так же у пользователя есть выбор каким методом искать корни. Результатом является приложение под операционную систему Windows, с графическим интерфейсом. Приложение А (обязательное) Листинг программы на языке Python Листинг файла main.py. ##файл в котором расписаны методы решения уравнений и само уравнение import math import peremennie ##импортируем нужные библиотеки def f(x): ##функция уравнения f = pow(x, 3) + peremennie.data1 * x + peremennie.data2 return f def fun_findkoren(a,b): ##функция нахождения корня методом половинного деления k = 0 f_a = f(a) f_b = f(b) while b-a > sigma and k < max_step: xm = a/2+b/2 f_xm = f(xm) if (f_a*f_xm <=0): b=xm f_b=f_xm else: a = xm f_a=f_xm return (a+b)/2 def method_chord3(x_prev, x_curr, e): ##функция нахождения корня методом хорд while math.fabs(x_curr - x_prev) > e: x_prev = x_curr - (x_curr - x_prev) * f(x_curr) / (f(x_curr) - f(x_prev)) x_curr = x_prev - (x_prev - x_curr) * f(x_prev) / (f(x_prev) - f(x_curr)) return x_curr sigma = 0.0000001 ##переменная погрешности max_step = 1000000 ##переменная максимального количества шагов Листингфайла my_prog.py. import sys import math import peremennie ##импорт нужных библиотек from PySide2.QtWidgets import QApplication, QWidget from main import f, method_chord3, fun_findkoren from ui.ui_main import Ui_form class MainWindow(QWidget): def __init__ (self, parent=None): QWidget.__init__(self, parent) self.ui = Ui_form() self.ui.setupUi(self) self.ui.pushButton.clicked.connect(self.h) ##при нажатии на кнопку срабатывает метод хорд self.ui.pushButton_2.clicked.connect(self.j) ##при нажатии на кнопку срабатывает половинного деленеия def h(self): ##функция для считывания чисел из полей ввода и вызова метода хорд peremennie.data1 = self.ui.lineEdit_2.text().replace(',', '.') peremennie.data2 = self.ui.lineEdit_3.text().replace(',', '.') peremennie.data1 = float(peremennie.data1) peremennie.data2 = float(peremennie.data2) peremennie.data3 = self.ui.lineEdit3.text().replace(',', '.') peremennie.data4 = self.ui.lineEdit_4.text().replace(',', '.') peremennie.data3 = float(peremennie.data3) peremennie.data4 = float(peremennie.data4) self.ui.result_lineEdit.setText(str(float('{:.4f}'.format(method_chord3(peremennie.data3,peremennie.data4, 0.0000001))))) def j(self): ##функция для считывания чисел из полей ввода и вызова метода половинного деления peremennie.data1 = self.ui.lineEdit_2.text().replace(',', '.') peremennie.data1 = float(peremennie.data1) peremennie.data2 = self.ui.lineEdit_3.text().replace(',', '.') peremennie.data2 = float(peremennie.data2) self.ui.result_lineEdit.setText(str(float('{:.4f}'.format(fun_findkoren(-1000000,1000000))))) if __name__ == '__main__': app = QApplication(sys.argv) window = MainWindow() window.show() sys.exit(app.exec_()) |
