Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени. Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24
 Скачать 1.58 Mb. Скачать 1.58 Mb.
|
|
Амиров Д.Ф. ЧИСЛЕННЫЕ МЕТОДЫ Методические указания по выполнению лабораторных и самостоятельных работ Содержание: Лабораторная работа №1 5 Решение алгебраических и трансцендентных уравнений с помощью инструментальных средств. Локализация корней уравнения. Метод деления отрезка пополам. 5 Лабораторная работа №2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы № 3, 4 24 Численное дифференцирование и интегрирование. 24 Метод трапеций. Метод Симпсона. 24 Лабораторные работы № 5, 6 45 Решение дифференциальных уравнений первого порядка. 45 Методы Эйлера и Рунге-Кутта. 45 Лабораторная работа №7 63 Точные методы решения систем алгебраических уравнений. Прямые методы решения систем линейных алгебраических уравнений: метод Гаусса. 63 Список литературы 96 Лабораторная работа №1Решение алгебраических и трансцендентных уравнений с помощью инструментальных средств. Локализация корней уравнения. Метод деления отрезка пополам.Цельработы:ознакомление с численными методами решения алгебраических и трансцендентных уравнений в вычислительной системе MathCAD. Формаотчетности:выполнениезаданий. Теоретическийматериал:Численные методы служат для нахождения приближенного решения математических задач. Анализ аналитических и численных методов решения алгебраических и трансцендентных уравнений показывает, что не существует единого алгоритма определения корней уравнения. Только их совокупность позволяет найти корни уравнений, и то не всегда. Компьютерные технологии решения алгебраических и трансцендентных уравнений представляют собой выполнение следующих математических процедур: определение области изоляции каждого из вещественных корней уравнения; выбор встроенной функции решения уравнения; решение уравнения; проверка достоверности полученного решения. Любое приближенное решение связано с ошибкой (погрешностью). Оценка точности результатов вычислений является важнейшим этапом организации вычисления. Это особенно важно при отсутствии опытных данных для сравнения. Рассмотрим источники погрешностей. Математическая модель никогда во всей полноте точно не отражает описываемый объект. Кроме того, некоторые данные, входящие в математическую модель могут иметь погрешность. Это погрешность математической модели. Такая погрешность называется неустранимой погрешностью. Погрешность численного метода решения. Часто получение точного решения требует неприемлемо большого числа арифметических операций. Вычислительная погрешность - связана с погрешностью округления чисел из-за ограниченности представления чисел в компьютере. Различают абсолютнуюи относительнуюпогрешности. Пусть а– точное, вообще говоря неизвестное числовое значение некоторой величины, а а*- известное приближенное значение этой величины, тогда величину: D(а*) = | а–а*| называют абсолютной погрешностью числа а*, а величину: d(а*) = – его относительной погрешностью. (а) | а При сложении и вычитании складываются абсолютные погрешности, а при делении и умножении – относительные погрешности.  Физическая интерпретация начальных задач для определенных видов уравнений лежит в основе машинно-графических методов приближенного решения. Название графическиеметоды говорит о приближенном представлении искомого решения у(х) на промежутке [xо,b] в виде графика, который можно строить по тем или иным правилам, связанным с графическим толкованием данной задачи. Физическая интерпретация начальных задач для определенных видов уравнений лежит в основе машинно-графических методов приближенного решения. Название графическиеметоды говорит о приближенном представлении искомого решения у(х) на промежутке [xо,b] в виде графика, который можно строить по тем или иным правилам, связанным с графическим толкованием данной задачи.Задача делится на 2 этапа: Локализация корня – т.е. нахождение интервала, на котором изолирован единственный нужный нам корень. Выбор интервала производится путем анализа знака F(x)в ряде пробных точек. Уточнение положения корня на интервале локализации. Свойства функции на интервале локализации [a, b]: f(x) непрерывна на [a, b] ; f(x) монотонна на [a, b] , т.е. f(x) 0 или f(x) 0, что обуславливает единственность корня ; f(x) меняет знак на [a, b], f(a) f(b) 0 , т.е. корень существует; f(x) не имеет точек перегиба, т.е. f (x) 0 или f (x) 0. Пример 1. Решим уравнение F(x) :ln(x) (x 1)3 методом деления отрезка пополам, с применением прикладного программного средства (MathCAD). Решение: 1. Отделим корни уравнения F(x) графическимметодом. Определим ОДЗ F(x) : для F(x) х>0. F(x) :ln(x) (x 1)3 Рассмотрим диапазон х :0.1 , 0.2 .. 1 х 0,1;1 . Вычисляем значения аргумента и функции: Х= F(x)  
 8.0 8.06.0 4.0  F( x) 2.0 2.000 x Рис1. Из таблицы: при x1 0,1: F(x1) 0,972; при x2 0,2: F(x2 ) 0,119. Функция меняет знак, следовательно, в данном интервале cсуществует корень уравнения. Из графика (рис.1): 0,1; 0,2 точка пересечения графика функции с осью ОХи есть приближенный корень уравнения, т.е. интервал, в котором находится искомый корень 0,1;1 . 2. Отделим корни уравнения F(x) методомделенияотрезкапополам. F(x) :ln(x) (x 1)3 ; Заданная точность: Е:=0.001 a:0.1; b:0.2    Согласно методу деления отрезка пополам: Согласно методу деления отрезка пополам:bisection (f a b) while a b E   c (a b) c (a b)2 b c if (f(a) f(c)) 0 Bisection (f, a, b)=0.187 a c (a b)  2 2otherwise Корень уравнения: х=0.187 Проверка: f(0.187) 0.004  Т.к. f (0.187) стремится к нулю, следовательно, считаем, что корень уравнения найден верно. Найдем относительную погрешность метода деления отрезка пополам: d(х) (х) / х0,001/ 0,187 0,005348 0,54%. Упражнение 1. Отделить корни заданного уравнения, пользуясь графическим методом. Задание выполнить с применением прикладного программного средства (MathCAD). Номер варианта при выполнении задания выдается преподавателем из Таблицы 1а. Задание шага может варьироваться в зависимости от величины выбранного участка и характера поведения функции F(x) . Примечание: Во многих случаях задачу графического отделения корня можно упростить, заменив исходное уравнение вида F(x) 0 равносильным ему уравнением f(x) f 1 2 . Упражнение 2. По методу деления отрезков пополам вычислить корни заданного уравнения с точностью e103:   с помощью «ручной» расчетной таблицы и калькулятора; с помощью «ручной» расчетной таблицы и калькулятора;с применением программного табличного редактора Ms’Excel; с применением прикладного программного средства MathCAD. При выполнении сначала уточнить корни заданного уравнения методом половинного деления с заданной точностью с помощью «ручной» расчетной таблицы. Примерная форма расчетной таблицы 1, которую можно использовать для организации «ручных» вычислений, представлена ниже. Таблица 1
Номер варианта при выполнении задания выдается преподавателем из таблицы 1а. Таблица 1а
Задания для самостоятельной работы Задание 1. Число x, все цифры которого верны в строгом смысле, округлить до трех значащих цифр. Для получения числа x1 x найти предельную абсолютную и предельную относительные погрешности в строгом и широком смысле. В записи числа x1 указать количество верных цифр по абсолютной и относительной погрешности (в строгом и широком смысле). Номер варианта при выполнении задания выдается преподавателем из таблицы 2. Задание 2. Вычислить значение величины Zпри заданных значениях параметров a,b,c, используя «ручные» расчетные таблицы для пошаговой регистрации результатов вычислений, двумя способами: с систематическим учетом границ абсолютных погрешностей; по способу границ. Найти абсолютную и относительную погрешности Z и определить количество верных цифр Z, если a,b,cверны в строгом смысле. Номер варианта при выполнении задания выдается преподавателем из таблицы 2. Задание 3. Вычислить значение величины Zпри заданных значениях параметров a, b, c, используя MathCAD, с пошаговой и итоговой регистрацией результатов вычислений. Найти абсолютную и относительную погрешности Z и определить количество верных цифр Z, если a,b,cверны в строгом смысле. Номер варианта при выполнении задания выдается преподавателем из таблицы 2. Сравнить полученные результаты между собой, прокомментировать различие методов вычислений и смысл полученных числовых значений.    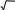     Таблица 2 Таблица 2
  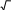 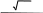      |
