Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени. Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24
 Скачать 1.58 Mb. Скачать 1.58 Mb.
|
Лабораторные работы № 5, 6Решение дифференциальных уравнений первого порядка.Методы Эйлера и Рунге-Кутта.Цель работы: научится применять численные методы для решения обыкновенных дифференциальных уравнений и систем дифференциальных уравнений различными методами; изучить влияние величины шага интегрирования на точность результатов разных методов; научиться применять встроенные в MathCAD средства для решения обыкновенных дифференциальных уравнений. Форма отчетности:выполнениезаданий. Дифференциальные уравнения устанавливают связь между независимыми переменными, искомыми функциями и их производными. Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным. Простейшим из численных методов решения дифференциальных уравнений является метод Эйлера. Это один из самых старых и широко известных методов. Метод Эйлера является сравнительно грубым методом решения дифференциальных уравнений, однако идеи, положенные в его основу, являются, по существу, исходными для очень широкого класса численных методов. Методы Рунге - Кутта обладают следующими отличительными свойствами: методы являются одноступенчатыми: чтобы найти значение функции в точке yi+1 нужна информация только о предыдущей точке (yi, xi); согласуются с рядом Тейлора вплоть до членов порядка hk, где степень kопределяет порядок метода; методы не требуют вычисления производных от f(x, y), а требуют вычисления самой функции. Метод Рунге-Кутта позволяет получить более точное решение дифференциального уравнения. Метод также часто используется для нахождения значений функций в нескольких начальных точках, что требуется в других, еще более эффективных численных методах. Преимущество метода Рунге-Кутта в том, что он совсем не использует предыдущую информацию. Каждый его шаг делается как бы заново, и для вычисления значения функции в точке xn+1 используется лишь ее значение в точке xn . Основным недостатком этого метода является его трудоемкость. Для получения следующего значения функции требуется несколько раз вычислять значение производной y′, т.е. обращаться к правой части дифференциального уравнения. Система MathCAD позволяет решать дифференциальные уравнения двумя принципиально различными способами: с помощью встроенных функций и непосредственно по формулам численных методов (Эйлера и Рунге – Кутта). Численное решение дифференциального уравнения первого порядка Y’=f(x,y)при начальных условиях Y(x0)=Y0по методу Эйлера находится в виде:
Значения X0и Y0являются начальными условиями решения уравнения. Первая строка таблицы при известном X0и шаге hвычисляется по соотношениям: X1=X0+h,X2=X1+h,…,Xn=Xn-1+h. Значения функции Y1, Y2, … , Ynвычисляются по рекуррентной формуле Эйлера: Yi+1=Yi+hf(xi,yi). Метод Эйлера основан на линейном разложении функции на участке. Пример 1. f(x y) ln(x) y x0 12 y0 5.2 y f(x y) a 12 h 0.2 a x0 b 14 i 0 10 yi fxi yi 
xi1 xi h x yi1 yi h yi 
y Самым популярным методом является алгоритм Рунге – Кутта 4-го порядка, успешно используемый для решения большинства дифференциальных уравнений. Численное решение дифференциального уравнения Y’=f(x,y)с начальным условием Y(x0)=Y0ищется в отдельных (называемых узловыми) точках промежутка [x0;x1], расстояние между которыми определяется величиной выбранного шага h. В точке xi+1значение искомой функции Y(xi+1) = Yi+1рассчитывается по формуле, исходя из полученного на предыдущем шаге значения функции Yi: yi1 : yi hk 6 1 2 k2 2 k3 k4 , k1 : fxi, yi k : h h 2 fxi 2 , yi 2 k1 где k : h h 3 fxi 2 , yi 2 k2 k : h h 4 fxi 2 , yi 2 k3 Метод Рунге – Кутта позволяет рассчитывать приращение функции на всем интервале [x0;x1].Исходя из условия Y(x0)=Y0, мы найдем значение Yiв точке Численное решение дифференциального уравнения представляет собой таблицу значений функции Yiв узловых точках xi. В MathCAD линейное дифференциальное уравнение можно решить с помощью встроенной функции rkfixed, реализующей алгоритм Рунге – Кутта 4- го порядка. Ввести ее можно с помощью команды меню Добавить – Функцию f(x). Эта функция требует задания нескольких параметров: rkfixed (y, x1, x2, npoints, D), где y - начальное значение в точке x1; x1 - начальная точка расчета; x2 - конечная точка расчета npoints - количество шагов, при котором численный метод будет решать систему (величина, обратная длине шага h); D - функция, содержащая правую часть уравнения ДУ. Результатом работы функции rkfixed является матрица, в первом столбце которой содержатся узловые точки переменной x, а во втором – рассчитанные в этих точках значения функции. Пример 2. Найти решение уравнения методом Рунге – Кутта в пяти точках отрезка [0;1] при h=0.1, удовлетворяющего условию y(0)=-1; 3 y2 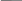  y' y'1 x 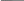 D(x y) D(x y) y:=-1 3 y2 1 x R rkfixed 1 0 1 1  0.1 0.1 D 
R Любые пять понравившихся точек вы можете выбрать по желанию. Если необходимо узнать значение функции в одной точке, то либо найдете нужный ряд в таблице при помощи строки прокрутки, либо используйте стандартную для MathCAD форму вывода с применением матричных индексов. При этом нужно учитывать, что точек, в которых были вычислены величины функции, на одну больше, чем было задано шагов: R5 1 0.451 Решения дифференциального уравнения – это использование встроенной функции odesolve, она также вводится с помощью команды меню Добавить – Функцию f(x). Рассмотрим этот вариант. Постановказадачи Дано дифференциальное уравнение n-го порядка и начальные условия его решения. Уравнение может быть линейным и нелинейным. Необходимо определить функцию Y=φ(x)и все ее производные, удовлетворяющие уравнению и начальным условиям. Решение нужно получить в виде таблиц и графиков функции и производных. Выборметодарешенияуравнения С целью получения высокой точности решения уравнения выполним методом Рунге – Кутта такого порядка, который обеспечивается системой MathCAD. Выборвстроеннойфункциирешениядифференциальногоуравнения Для решения линейного и нелинейного дифференциального уравнения n-го порядка в MathCAD имеется встроенная функция odesolve(x,b,n),где x – аргумент искомой функции Y(x) b – конец интервала интегрирования n – число шагов интегрирования с постоянным шагом. Технологиярешениядифференциальногоуравнения: вводится слово Given,указывающего на то, что далее следует решаемое дифференциальное уравнения и его начальные условия; ввод дифференциального уравнения в произвольном виде, например:  d2 Y(x) d2 Y(x) 2 x d Y(x) 1.2 Y(x) x e x dx2 dx , или так  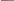  d2 Y(x) 2 x d Y(x) 1.2 Y(x) x e x 0 d2 Y(x) 2 x d Y(x) 1.2 Y(x) x e x 0 dx2 dx2 dx , или так Y''(x) 2 x Y'(x) 1.2 Y(x) x ex |
