Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени. Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24

• Название: Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24
• Дата: 23.03.2022
• Размер: 1.58 Mb.
• Имя файла: Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени.docx
• Тип: Лабораторная работа; #410752
• страница: 10 из 15

Лабораторная работа №7

Точные методы решения систем алгебраических уравнений. Прямые методы решения систем линейных алгебраических уравнений: метод Гаусса.

Цель работы: ознакомление с численными методами решения систем алгебраических уравнений в вычислительной системе MathCAD.

Форма отчетности:выполнениезаданий.
Системы уравнений могут быть линейными и нелинейными, с постоянными и переменными коэффициентами. Решение таких уравнений возможно аналитическими и численными методами. Все методы решения систем линейных алгебраических уравнений можно разделить на две основные группы. К первой относятся так называемые прямые (или матричные) методы: Крамера и Гаусса. Во вторую группу входят довольно специфические итерационные методы. В системе MathCAD реализованы в виде специальных функций методы обеих групп.
Пример 1. Решить СЛАУ методом Гаусса.

1.2 x₁ 

0.22 x₂  0.1 x₃ 

0.1 x₄  0.1 x₅ 20

0.1 x₁  1.3 x₂  0.03 x₃  0.1 x₄  0.2 x₅ 3

0.15 x₁  0.1 x₂  0.8 x₃ 

0.1 x₄ 

0.1 x₅

3.9

0.5 x₁  0.1 x₂  0.28 x₃  0.94 x₄  0.1 x₅ 5

0.2 x₁  0.3 x₂  0.2 x₃  0.1 x₄  0.93 x₅ 9
Решение:
Задаем коэффициенты а_{i, j} :

_1.2

0.22

0.1

0.1

0.1 _

_ 0.1

1.3

0.03

0.1

0.2 _

A  _ 0.15

^ 0.5

0.1

0.1

0.8

0.28

0.1

0.94

0.1 _

0.1 ^

_0.2

0.3

0.2

0.1

0.93 _

Задаем свободные коэффициенты b_i :

_ 20 _

 ³ 

B  _ 3.9 _

 ₅ 

 ⁹ 

1способ:Сформируем расширенную матрицу системы (Rm).

Rm:augment( A, B)

_1.2

0.22

0.1

0.1

0.1

20 _

_ 0.1

1.3

0.03

0.1

0.2 3 _

Rm  _ 0.15

^ 0.5

0.1

0.1

0.8

0.28

0.1

0.94

0.1 3.9 _

0.1 5 ^

_0.2

0.3

0.2

0.1

0.93 9 _

Приводим полученную расширенную матрицу к ступенчатому виду.

st:rref(Rm)

_1 0 0 0 0

_0 1 0 0 0

st  _0 0 1 0 0

^0 0 0 1 0

_0 0 0 0 1

16.86 _

2.248 _

9.766 _

11.615 ^

4.475

Формируем вектор – столбец решения системы уравнений.

x:submatrix(st, 0 , 4 , 5 , 5)





X  _

16.86 _

2.248 _

9.766 _

^ 11.615 ^

_ 4.475 _

2 способ:
S( A  B) 	c  d  x 	augment ( A  B) rref ( c) submatrix ( d  0  4  5  5)





S( A  B)  _

16.86 _

2.248 _

9.766 _

^ 11.615 ^

Проверка:

_ 4.475 _

Матричный способ:

x:A^1 B




16.86 _

2.248 _

x  _ 9.766 _

^ 11.615 ^

_ 4.475 _
Пример 2. Метод Крамера

A  1.04

_ 20
0.22
0.1
0.1
0.1 _

_ 3 1.3

0.03

0.1

0.2 _

1 

_ 3.9 0.1

^ 5 0.1

_ 9 0.3

0.8

0.28

0.2

0.1

0.94

0.1

0.1 _

0.1 ^

0.93 _

1  17.532

_ 1.2 20

0.1

0.1

0.1 _

_ 0.1

3 0.03

0.1

0.2 _

2 

_ 0.15

^ 0.5

3.9 0.8

5 0.28

0.1

0.94

0.1 _

0.1 ^

2  2.338

_ 0.2 9

0.2

0.1

0.93

_1.2

0.22 20

0.1

0.1 _

_ 0.1

1.3 3

0.1

0.2 _

3 

_ 0.15

^ 0.5

0.1 3.9

0.1 5

0.1

0.94

0.1 _

0.1 ^

3  10.156

_0.2

_1.2

0.3 0.22

9

0.1

0.1

20

0.93 _

0.1 _

_ 0.1

1.3

0.03

3 0.2 _

4 

_ 0.15

0.1

0.8 3.9 0.1 _

4  12.078

^ 0.5

0.1

0.28 5

0.1 ^

_0.2

_1.2

0.3 0.22

0.2

0.1

9

0.1

0.93 _

20 _

_ 0.1

1.3

0.03

0.1 3 _

5 

_ 0.15

^ 0.5

0.1

0.1

0.8

0.28

0.1 3.9 _

0.94 5 ^

5  4.654

_0.2

0.3

0.2

0.1 9 _

1

x₁ 

A

2

x₂ 

A

3

x₃ 

A

4

x₄ 

A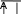

5

x₅ 

x₁  16.86 x₂  2.248 x₃  9.766 x₄  11.615 x₅  4.475

При помощи встроенной функции:

x:isolve( A,





x  _

B)

16.86 _

2.248 _

9.766 _

^11.615 ^

_ 4.475 _
Точность:

_ 16.86 <sub>

</sub> 2.248 _

x  _ 9.766 _

^11.615 ^

_ 4.475

^ 4  10<sup> 5 

</sup> 8  10^{ 5 }

 

^{A x  B } 4  10^{ 4 }





^1.2  10^{ 4 }

_1.5  10^{ 4}