Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени. Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24

• Название: Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24
• Дата: 23.03.2022
• Размер: 1.58 Mb.
• Имя файла: Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени.docx
• Тип: Лабораторная работа; #410752
• страница: 9 из 15

Примечание:

1. 
   Шаблон производной можно ввести, используя панель инструментов Матанализ.
   
2. 
   Для вывода на экран знака (‘) (штрих) используется комбинация клавиш
   

+, повторное нажатие приведет к отображению (“).

3. 
   Вводятся начальные условия: Y(x0)=Y0, Y’(x0)=Y’0;
   
4. 
   Вводится встроенная функция odesolve (x, b, n) с присвоением ей уникального имени и с численными значениями b и n;
   
5. 
   Получение решения нажатием клавиши .
   

Решение будет вычислено и находится в памяти компьютера. Теперь его можно вывести на экран в виде таблицы. Для этого необходимо:

1. 
   присвоить переменной x значения, соответствующие желаемому диапазону изменения функции Y(x);
   
2. 
   ввести имя, присвоенное функции odesolve;
   
3. 
   нажать клавишу <=> для получения решения в виде таблицы.
   

Получить график функции и ее производных можно обычным для MathCAD

способом.

Пример 3. Необходимо решить дифференциальное уравнение:

^d2 Y(x)

 ^2 x ^d Y(x) ^ 1.2 Y(x)

x e^{ x}

dx²

_ dx _

При начальных условиях Y(0)=1, Y’(0)=0.

Решение представить в виде таблицы и графика функции Y(x).

Решение:

Given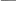

^d2 Y(x)

 ^2 x ^d Y(x) ^
1.2 Y(x)

x e^{ x}

dx²

_ dx _

Y(0) 1 Y'(0) 0

y Odesolve(x 10 200)

x 0 0.5 5

y(x) 
y(x)


^d y(x) dx


_d2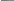

y(x)

dx²


1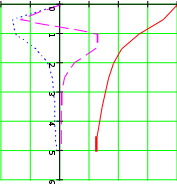

0.75

0.5

0.25

0.25

1
0.88
0.669
0.524
0.453
0.414
0.385
0.359
0.337
0.317
0.299

0.5
x

Пример 4. Найти решение обычного дифференциального уравнения

^d y( x) cos(x) 

dx

1


y( x)

на интервале [0, 100]. Функция имеет такие начальные

условия: у(0)=1.

Решение:

1. 
   Ввести ключевое слово Given.
   

2. 
   Записать, используя логический знак равенства, следующее выражение:
   

^d y( x) cos(x) 

d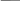x

1

.

y( x)

3. 
   Начальное условие записать следующим образом, используя логический знак равенства:
   

у(0)=1.

4. 
   Вычислить числовое решение задачи через использование функции
   

Odesolve:

у:=Odesolve(х,100).

5. 
   Построить график функции в точках интервала и отформатировать его.
   

Given

^d y(x) dx

y(0) 1

cos (x) 

1


y(x)

y Odesolve (x 100)

y(5) 2.302

y(35)

 8.011

x 

0 

100

Упражнение 1.
y(x)

15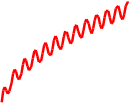




13.5

12

10.5

9

7.5

6

4.5

3

1.5

0

0 10 20 30 40 50 60 70

x

а; b

Решить задачу Коши для дифференциального уравнения y=f(x,y)на отрезке при заданном начальном условии и шаге интегрирования h.

При выполнении лабораторной работы № 5. Решить заданное

дифференциальное уравнение методом Эйлера с шагом 2h и с шагом hс применением:

1. 
   расчетной таблицы и калькулятора;
   

2. 
   программного табличного редактора Ms’Excel;
   
3. 
   прикладного программного средства MathCAD
   

Свести результаты вычисления в одну таблицу и сопоставить точность полученных значений функции. Значения искомой функции в соответствующих узлах сравнить между собой, и составить представление о точности полученного результата. По вычисленной таблице функции построить точечный график (ломаную Эйлера) и провести плавную кривую.

С помощью прикладного программного средства (MathCAD) методом Эйлера обеспечить вывод полученных решений в виде таблиц и графиков.

При выполнении лабораторной работы № 6 решить заданное дифференциальное уравнение методом Рунге – Кутта:

1. 
   с помощью «ручной» расчетной таблицы и калькулятора;
   
2. 
   с применением программного табличного редактора Ms’Excel;
   
3. 
   с применением прикладного программного средства MathCAD
   

Составить программу, которая запускается дважды – для шага hи шага h/2

(на одном и том же отрезке интегрирования а;b). Путем сравнения

полученных значений сделать вывод о точности результата, которая сопоставляется с точностью интегрирования по методу Эйлера. Обеспечить вывод полученных решений в виде таблиц и графиков.

Исходные данные для задания содержатся в таблице 8.
Таблица 8

Вариант	y=f(x,y)	a	B	y0	h
1.	xy3-x2	24	5	0.7	0.1
2.	4x2  1  3y2	2.6	4.6	1.8	0.2
3.	cos(1,5x-y2)-1,3	-1	1	0.2	0.2
4.	x2+xy+y2	2	3	1.2	0.1
5.	e  2x	0	0.5	0.3	0.05
6.	cos(1,5y+x)2+1,4	1	2	0.9	0.1
7.	4,1x-y2+0,6	0.6	2.6	3.4	0.2
8.	1  2 у1  х3 у	1.5	2	2.1	0.05
9.	x cos y 11	2.1	3.1	2.5	0.1
10.	2xy 0,4 x 4	3	5	1.7	0.2
11.	2,5x+cos(y+0,6)	1	3	1.5	0.2
12.	x+2,5y2+2	1	2	0.9	0.1
13.	2-sin(x+y)2	2	3	2.3	0.1
14.	2  х 1 х 2	0.1	0.5	1.25	0.05
15.	х cos y 2	-2	-1	3	0.1

16.	x2  0,5 y2  1	0	2	2.9	0.2
17.	sin(x+y)+1,5	1.5	2.5	0.5	0.1
18.	1  x 3 x 16,7	1.5	2	1.4	0.05
19.	e2x+0,25y2	0	0.5	2.6	0.05
20.	0,4x2+y2	1	3	1.8	0.2
21.	3x2  0,1xy	0	1	0,2	0,1
22.	0,185(x2  cos(0,7x))  1,843y	0,2	1,2	0,25	0,1
23.	x cos(y) 3	1,6	2,6	4,6	0,1
24.	x sin(y1) 13	0,2	1,2	1,1	0,1
25.	x cos(y) e	1,4	2,4	2,5	0,1
26.	x2  cos(y) p	1,7	2,7	5,3	0,1
27.	 3y 4x2  1	2,6	4,6	3,5	0,2
28.	2  sin2 (x y)	2	3	2,3	0,1
29.	1,6x 0,5y2	0	1	0,3	0,1
30.	x cos( y) 5	1,8	2,8	2,6	0,1

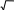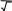Задания для самостоятельной работы
Задание 1. Найти решение обычного дифференциального уравнения

y^/=f(x,y) с использованием «блока решений».

1. 
   Ввести ключевое слово given(дано), с которого начинается блок решений.
   
2. 
   Записать уравнение, используя знак логического равенства между правой и левой частями уравнения с панели управления Вычисление.
   
3. 
   Задать начальные значения переменной, которая есть в уравнении.
   
4. 
   Ввести ключевое слово Odesolve, которым заканчивается блок решений, то есть присвоить функции, относительно которой решается уравнение, значение Odesolveс параметрами интервала интегрирования.
   
5. 
   Определить значение найденной функции в точках интервала, для чего создать соответствующий цикл.
   
6. 
   Построить и отформатировать график найденной функции в точках интервала.
   

Задание 2. Найти решение обычного дифференциального уравнения с использованием встроенной функции rkfixed.

1. 
   Задать начальные значения переменной, которая есть в уравнении.
   

2. 
   Записать уравнения, используя знак логического равенства между правой и левой частями уравнения с панели управления Вычисление.
   
3. 
   Задать количество шагов интегрирования уравнения на интервале.
   
4. 
   Присвоить функции, относительно которой решается уравнение, значение rkfixed с параметрами: функция, интервал интегрирования, количество шагов на интервале интегрирования, оператор дифференциального уравнения.
   
5. 
   Определить значение найденной функции в точках интервала, для чего создать соответствующий цикл.
   
6. 
   Построить и отформатировать график найденной функции в точках интервала.
   

Исходные данные для самостоятельной работы содержатся в таблице 9.

Таблица 9

Номер варианта	Уравнение f(x,y)	Начальные условия	Интервал нахождения решения	Шаг изменения
1	2	3	5	5
1	y cos(x) ln(y)	y(1)=1	[1,10]	1
2	tg(x)t(y)	y(0)=0	[0,5]	0.5
3	y 1  x2	y(1)=1	[1,7]
4	e  x y y	y(1)=1	[1, 5]	0.25
5	cos(x-2y)-cos(x+2y)	y(0)=/4	[0,4]	/2
6	2e-xcos(x)-y	y(0)=0	[0;3,5]	0,1
7	e-2ycos(x)-y	y(0)=0	[0;1]	0,05
8	lnx+2,5xsin(x)	y(0)=2,5	[1;3,5]	0,2
9	e35ysin(x)+y	y(0)=0	[0;1,5]	0,1

10	x2ln(x+y2)	y(0)=3,5	[1,2;2,4]	0,08
11	x2  ycos(x)	y(0)=3,6	[4,1;6,7]	0,1
12	sin(x)+cos(y2)	y(0)=2,2	[0,8;3,2]	0,1
13	e-2xsin(x+y)	y(0)=16,2	[4,8;6,4]	0,1
14	0,7y+xln(x+y)	y(0)=2,5	[12,4;14,1]	0,08
15	0,5x+ye(x-y)	y(0)=3,1	[8,5;9,7 ]	0,05
16	x2+ycos(x)	y(0)=1,4	[0;2,3]	0,1
17	y2-exy	y(0)=1,7	[2,4;3,5]	0,05
18	xy-e(x-y)	y(0)=2,8	[1,6;3,1]	0,1
19	sin(xy)-e2x	y(0)=5,7	[14,5;16,3]	0,05
20	x2  exy	y(0)=1,6	[5,2;6,8]	0,1
21	y/ln(y)	y(2)=1	[2;5]	0,25
22	e(x+y)-e(x-y)	y(0)=0	[0;2.5]	0,1
23	 1 cos(2 x) 1  sin(( y)	y(/4)=0	[/4, 3]	/8
24	1  1 x2 y	y(1)=0	[1;4]	0.3
25	sin(3x)-ytg(3x)	y(0)=1/3	[0,4]	0,25
26	cos(x-4y)-cos(x+4y)	y(0)=/4	[0,4]	/2
27	2e-xcos(x)y	y(0)=0	[0;3,5]	0,1
28	e-2ycos(x)+y	y(0)=0	[0;1]	0,05
29	lnx+sin(x)	y(0)=2,5	[1,5;3,5]	0,2
30	ey+2sin(x)	y(0)=0	[0;1,5]	0,1