Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени. Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24

• Название: Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24
• Дата: 23.03.2022
• Размер: 1.58 Mb.
• Имя файла: Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени.docx
• Тип: Лабораторная работа; #410752
• страница: 12 из 15

Пример 4. Решение СЛАУ методом последовательных приближений.

Дана СЛАУ:

1.2 x₁ 
0.22 x₂  0.1 x₃ 
0.1 x₄  0.1 x₅ 20

0.1 x₁  1.3 x₂  0.03 x₃  0.1 x₄  0.2 x₅ 3

0.15 x₁  0.1 x₂  0.8 x₃ 

0.1 x₄ 

0.1 x₅

3.9

0.5 x₁  0.1 x₂  0.28 x₃  0.94 x₄  0.1 x₅ 5

0.2 x₁  0.3 x₂  0.2 x₃  0.1 x₄  0.93 x₅ 9
Преобразуем СЛАУ:

₁₎ (1.2 

1) x₁ 

0.22 x₂  0.1 x₃ 

0.1 x₄  0.1 x₅

20  x₁

0.1 x₁ 

(1.3 

1)x₂ 

0.03 x₃  0.1 x₄  0.2 x₅

3  x₂

0.15 x₁  0.1 x₂ 

(0.8 

1) x₃ 

0.1 x₄ 

0.1 x₅

3.9  x₃

0.5 x₁  0.1 x₂  0.28 x₃ 

(0.94 

1)x₄ 

0.1 x₅

5  x₄

0.2 x₁  0.3 x₂  0.2 x₃ 

0.1 x₄ 

(0.93 

1) x₅

9  x₅

₂₎ 0.2 x₁ 

0.22 x₂  0.1 x₃ 

0.1 x₄  0.1 x₅

20  x₁

0.1 x₁  0.3 x₂ 

0.03 x₃  0.1 x₄  0.2 x₅

3  x₂

0.15 x₁  0.1 x₂ 

0.2 x₃ 

0.1 x₄ 

0.1 x₅

3.9  x₃

0.5 x₁  0.1 x₂  0.28 x₃ 

0.06x₄ 

0.1 x₅

5  x₄

0.2 x₁  0.3 x₂  0.2 x₃ 

0.1 x₄ 

0.07 x₅

9  x₅

^{3) x}1

20  0.2 x₁ 

0.22x₂  0.1 x₃ 

0.1 x₄  0.1 x₅

x₂ 3 

0.1 x₁  0.3 x₂ 

0.03x₃  0.1 x₄  0.2 x₅

x₃ 3.9 

0.15x₁  0.1 x₂ 

0.2 x₃ 

0.1 x₄ 

0.1 x₅

x₄ 5 

0.5 x₁  0.1 x₂  0.28x₃ 

0.06x₄ 

0.1 x₅

x₅ 9  0.2

x₁  0.3 x₂  0.2 x₃ 

0.1 x₄ 

0.07 x₅

Проверка условия сходимости:

0.2		0.22				0.1			0.1  0.1	1
0.1		0.3			0.03				0.1  0.2	1
0.15			0.1			0.2			0.1  0.1	1
0.5		0.1			0.28				0.06  0.1	1
0.2		0.3			0.2			0.1  0.07		1

Условие сходимости выполняется. Задаем свободные коэффициенты а_{i, j} :

_0.2

_ 0.1

A _0.15

^ 0.5

_0.2

0.22

0.3

0.1

0.1

0.3

0.1 0.03

0.2

0.28

0.2

0.1

0.1 0.1

0.06

0.1

0.1 _

0.2 _

0.1 _

0.1 ^

0.07

Задаем свободные коэффициенты b_i :

_ 20 _

 ³ 

B  _3.9 _

 ₅ 

 ⁹ 

Заданная точность: e:0.001

Проверяем достаточное условие сходимости.

Norme (A)=0.948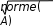

a: a

a1

0.974

Достаточное условие сходимости выполняется.

Задаем начальные приближения: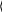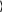

x⁰ :B

Задаем количество итераций: к:=0..15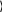

Итерационные формулы для вычисления приближений:

_xк1

:B А х^к

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	20	15.87	17.406	16.594	16.926	16.806	16.88	16.85	16.865	16.857	16.861	16.859	16.86	16.86	16.86	16.86
1	3	1.917	1.905	2.243	2.18	2.281	2.234	2.258	2.243	2.25	2.247	2.249	2.248	2.248	2.248	2.248
2	3.9	8.78	9.771	9.965	9.811	9.782	9.759	9.766	9.765	9.767	9.766	9.767	9.766	9.767	9.766	9.766
3	5	14.808	11.618	12.002	11.455	11.639	11.58	11.626	11.61	11.618	11.614	11.616	11.615	11.615	11.615	11.615
4	9	4.45	5.287	4.525	4.532	4.461	4.474	4.473	4.475	4.475	4.475	4.475	4.475	4.475	4.475	4.475

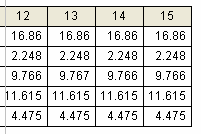x

^^x



k 1

^{  ( xk}

₀

) ₀  ( x

k 1

) ₁  ( x^k

) ₁ 

^^x





k 1

^{  ( xk}



2

) ₂ 

• 
  ( x
  

k 1

) ₃  ( x^k

) ₃ 

^^x



k 1

^{  ( xk) 4} 4

	0
0	24.451000
1	6.565460
2	2.490434
3	1.103528
4	0.504047
5	0.215564
6	0.108433
7	0.049615
8	0.025908
9	0.013094
10	0.006485
11	0.003434
12	0.001740
13	0.000890
14	0.000461
15	0.000235

Полученное тринадцатое значение суммы модулей разности (0,00089) при

e0,0001 удовлетворяет условию. Значит, что 13 столбец значений х

является решением СЛАУ.

x₁   16 ,860 ;

x₂   2,248 ;

x₃   9,766 ;

x₄   11,615 ;

x₅  4,475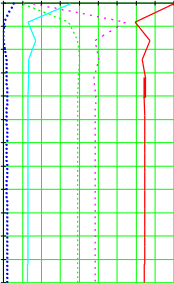

20

_x ^k^





_x ^k^


_x ^k^

17.99


15.98

0


13.97

1



11.96

2



3
_x ^k^





_x ^k^ _

9.95
7.94

4

5.93
3.92
^1.9 0 1.25 2.5 3.75 5 6.25 7.5 8.75 10 11.25 12.5 13.75 15

k

trace 1

trace 2

trace 3

trace 4

trace 5


i
Зависимость x ^(k) (i=0..4) от количества итераций (к)
Пример 5. Найти решение системы уравнений с использованием soln.



^{2 x y 2 z1}

_2 x y 3z1



^5x y 4 z3.

Решение:

1. 
   Создать матрицу А:
   

2

А:= 2

5
 1 2

 1 3 .

 1 4

2. 
   Создать вектор b:
   

1

b:= ¹ .

 3

3. 
   Найти решение системы, используя функцию soln:
   

	2	 1	2	 1 1
soln1	2	 1	3	 1	.
	5	 1	4	 3
4. Результат решения:

2	1	2
A  2	1	3
5	1	4
		 1

b 

_1

1

_3


_1.333

soln ₁  A b

soln₁ 

3.667

_ 0
Пример 6. Найти решение системы уравнений с использованием «блока решений» given…find.


^{2 x y 2 z1}

_2 x y 3z1



^5 x y 4 z3.

Решение:

1. 
   Задать начальные значения переменным, которые присутствуют в уравнении.
   

x=0; y=0; z=0.

2. 
   Ввести ключевое слово given(дано), с которого начинается блок решений.
   
3. 
   Записать уравнение, используя знак логического равенства между правой и левой частями уравнения из панели управления Вычисление.
   


^{2 x y 2 z1}

_2 x y 3z1



^5x y 4 z3.

4. 
   Ввести ключевое слово find (найти), которым заканчивается блок решений.
   

find(x,y,z) =

5. 
   Результат решения:
   

x  0

y  0

z  0

given

2x  y  2z 2x  y  3z 5x  y  4z

1

1

3

_1.333_

find (x y z)  3.667

_ 0
Пример 7. Найти решение системы уравнений с использованием встроенной функции lsolve.



^{2 x y 2 z1}

_2 x y 3z1



^5 x y 4 z3.

Решение:

1. 
   Создать матрицу А:
   

2. 
   Создать вектор b :
   

2

A: 2

5

b: 
 1 2

 1 3 _.

 1 4
1

1 _.

 3

3. 
   Найти решение системы, используя функцию lsolve:
   

_2

A  2

_5

1 2 _

1 3

1 4
b 

¹ 

1

_3

lsolve(A  b) 

_1.333

3.667

_ 0

Пример 8. Найти решение системы уравнений с использованием функции