Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени. Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24

• Название: Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24
• Дата: 23.03.2022
• Размер: 1.58 Mb.
• Имя файла: Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени.docx
• Тип: Лабораторная работа; #410752
• страница: 2 из 15

Лабораторная работа №2

Метод Ньютона (касательных). Метод итерации.

Цельработы:ознакомление с численными методами решения алгебраических и трансцендентных уравнений в вычислительной системе MathCAD.

Формаотчетности:выполнениезаданий.

В методе Ньютона в качестве x₀выбирается одна из границ интервала [a,b] и из этой точки строится касательная. В качестве приближенного значения корня x₁ принимается точка пересечения касательной с осью абсцисс.

Из точки (x₁,f(x₁))проводится новая касательная и т. д., до достижения

заданной точности f(x_n e) f(x_n e) 0 .

Уравнение касательной в точке x_nимеет вид:

y_k(x)  f(x_n)  f

(x_n)

(x x_n) _,

y_k(x_n1) 0 _,

отсюда следует итерационный процесс:

x j(x

) x

f(x_n)



. (1)

n
n 1

ⁿⁿf^(x)

Выражение для начальной точки x₀совпадает с:


^a, если

с

f(a) f

(a) 0 _.





b, если

f(b) f

^(b) 0

Метод Ньютона можно считать модификацией метода простой итерации

xj

10. 
    при
    

j(x) x^f(x) .

f ^(x)

Условия сходимости метода следуют из j

(x)

1, а именно, для всех xиз

области локализации корня должно выполняться
f(x) f^''(x)

'
q 1

( f(x))²

(2)

Из (2) следует, что чем меньше область локализации корня, тем меньше знаменатель q сходимости метода Ньютона и в пределе q→0при x→x^*. Таким образом, при достаточно малой области локализации корня сходимость метода Ньютона безусловная.

Пример 1. Вычислить корни заданного уравнения F(x)с точностью

^{e10 6} ,

используя метод Ньютона (касательных) с применением прикладного программного средства (MathCAD).

F(x):ln(x) (x1)³ ;

a:0.1;

^b:0.2,

Решение: Вычисление корней заданного уравнения методом Ньютона

(касательных).

F(x):ln(x)(x1)³ ;

a:0.1;

b:0.2

Заданная точность: ^{E:0.000001}

pr(x)-производная функции

f(x) _:

pr(x): ^d

dx

f(x).

Определяем начальную точку:

x_nt a

if a 

f(a) _b

pr(a)

b otherwise
x_ nt0.1

Согласно методу Ньютона (касательных ), находим:

q(x) :x

x:x_ nt

t :q(x)

f(x)


pr(x)

y(xe) 

while

x

t 

t  x E t

q(x)

t

y (0.1 , 0.000001) = 0.187111

Корень уравнения: х = 0.187111

Проверка:

f(0.187111) 0.003138

Т.к. ^{f (0.187111)} стремится к нулю, следовательно, считаем, что корень уравнения найден, верно. Найдем относительную погрешность метода Ньютона (касательных):

d(х) (х) / х0,000001/ 0,187111 0,000005344 0,00053%.

Пример 2. Вычислить корни заданного уравнения F(x), с точностью

e10^{ 6} ,

используя метод простой итерации с применением прикладного программного средства (MathCAD).

F(x):ln(x)(x1)³ ;

a:0.1;

^b:0.2 .

Решение: Вычисление корней заданного уравнения методом итераций.

F(x):ln(x) (x1)³ ;

a:0.1;

b:0.2

Задаем: h:=0.01 , заданная точность: e:10^6 .

х:а, а  h.. b, т.е. ^{х:0.1, 0.11, .., 0.2}

Находим значение функции

F(x)

в интервале

0,1; 0,2 :

х= F(x) =

	0			0
0	0.1		0	-0.971585
1	0.11		1	-0.839644
2	0.12		2	-0.715336
3	0.13		3	-0.597324
4	0.14		4	-0.484569
5	0.15		5	-0.376245
6	0.16		6	-0.271685
7	0.17		7	-0.170344
8	0.18		8	-0.071766
9	0.19		9	0.024428
10	0.2		10	0.118562

Находим значение производной функции

F(x)

в интервале

0,1; 0,2 :

pr(x): ^d

dx

f(x)

pr(x)

	0
0	13.63
1	12.787209
2	12.096533
3	11.523008
4	11.041657
5	10.634167
6	10.2868
7	9.989053
8	9.732756
9	9.511458
10	9.32

Находим минимальное значение функции

f(x)на интервале

0,1; 0,2 :

min

min

f:min( pr(a) ),

f0.932

pr(b) )

Находим максимальное значение функции

f(x)на интервале

0,1; 0,2 :

max

f:max( pr(a) ,

pr(b) ) ;

max f

13.63.

Находим параметр a:

a:
min

1

f max f^;

a0.043573.

Запишем в обратном виде преобразованную функцию:

f(x) :x a f(x)

pr2(x) - производная функции

f(х):

pr2(x):1 a

pr(x)

Определяем начальную точку:

x_nt 

b if

pr2 ( a)

• 
  pr2 ( b )
  

a otherwise
_ nt0.1

Определяем критерий точности: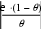

q:max fq13.63

A:
A9.266 10^6
Предположим i:=1..25

x₀ :x_ ntx₀ 0.1

x_i:f

(x_i1)

x_i x_i1 

	0
0	0.1
1	0.142335
2	0.162331
3	0.173128
4	0.179195
5	0.182664
6	0.184665
7	0.185825
8	0.186499
9	0.186891
10	0.187119
11	0.187253
12	0.18733
13	0.187376
14	0.187402
15	0.187417
16	0.187426
17	0.187432
18	0.187435
19	0.187436
20	0.187437
21	0.187438
22	0.187438
23	0.187439
24	0.187439
25	0.187439

	0
0	0.042
1	0.02
2	0.011
3	6.067·10 -3
4	3.469·10 -3
5	2.001·10 -3
6	1.16·10 -3
7	6.74·10 -4
8	3.923·10 -4
9	2.285·10 -4
10	1.332·10 -4
11	7.765·10 -5
12	4.528·10 -5
13	2.64·10 -5
14	1.54·10 -5
15	8.979·10 -6
16	5.237·10 -6
17	3.054·10 -6
18	1.781·10 -6
19	1.039·10 -6
20	6.059·10 -7
21	3.534·10 -7
22	2.061·10 -7
23	1.202·10 -7
24	7.01·10 -8

x 

Так как

^x21 ^{ x}20

6.059 10 ^7

A9.266 10 ^6 ,

то искомый корень уравнения

найден, x=x₂₁=0,187438.



Т.к. f (0.187438) стремится к нулю, следовательно, считаем, что корень уравнения найден верно. Найдем относительную погрешность метода итераций:

d(х) (х) / х0,000001/ 0,187438 0,000005335 0,00053%.
Проверка: f(0.187438)=-0.000009

Упражнение 1. Вычислить корни заданного уравнения с точностью

e10^{ 6} , используя метод простой итерации с помощью:

1. 
   расчетной таблицы и калькулятора;
   
2. 
   программного табличного редактора Ms’Excel;
   
3. 
   прикладного программного средства MathCAD.
   

При выполнении задания исходное уравнение привести к виду x f(x)

таким образом, чтобы на выбранном для выполнения задания отрезке

a; b

функция

x f(x)

удовлетворяла условию: существует такое число q,

0 q1,

что для любых

x a; b

имеет место

f^(x) q. Номер варианта при выполнении

выдается преподавателем из таблицы 3.
Упражнение 2. Вычислить корни заданного уравнения с точностью

e10^{ 6} , используя метод Ньютона с помощью:

1. 
   «ручной» расчетной таблицы и калькулятора;
   
2. 
   программного табличного редактора Ms’Excel;
   
3. 
   прикладного программного средства MathCAD.
   

Номер варианта при выполнении выдается преподавателем из таблицы 3.