Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени. Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24

• Название: Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24
• Дата: 23.03.2022
• Размер: 1.58 Mb.
• Имя файла: Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени.docx
• Тип: Лабораторная работа; #410752
• страница: 5 из 15

Формула парабол (Симпсона):

b _h


3
_f(x)dx ( y₀  4 y₁  2 y₂  4 y₃  2 y₄  4 y₅   4 y_n1  y_n)

a

В этой формуле ординаты с нечетными индексами умножаются на 4, с четными на 2. Предполагается, что n – число четное. При нечетном n формула имеет вид:

b _h


3
_f(x)dx ( y₀  4 y₁  2 y₂  4 y₃  2 y₄  4 y₅   2 y_n1  y_n)

a

Система MathCAD позволяет вычислять определенные интегралы в аналитическом и численном виде. Их технологии идентичны и отличаются лишь способом вывода результатов интегрирования.
Технология вычисления определенного интеграла состоит в выполнении следующих действий:

1. 
   вывод на экран шаблона определенного интеграла путем одновременного нажатия клавиш <Shift>+<&> или щелчка на кнопке определенного интеграла панели инструментов Исчисление;
   
2. 
   ввод в пустые маркеры подынтегральной функции, переменной интегрирования и значений пределов интегрирования;
   
3. 
   исполнение команды вычисления интеграла. Система MathCAD допускает использование трех следующих способов вызова команды вычисления интеграла:
   

• 
  клавиша <=> (равно),
  
• 
  совокупность клавиш <Shift>+<F9>,
  
• 
  вызова знака символьных вычислений <> (стрелка вправо).
  

Пример 1. Рассмотрим решения определенного интеграла методом трапеций:

p

2

^{Дан интеграл} ^{cos(2 * x)dx, f(x):=cos(2·x), интервал интегрирования [a, b],}

p

4

количество разбиений n:=25.
_{Решение:} f(x) cos (2x)

a  0.785

b 1.571

^ 0.785

4
^ 1.571

2

n 25

x_i a 
i 0 n

h i
k 1 (n  1)

_{h } ba

n

y_i f_x_i

g  ^h

2

y₀ 

_2 y _k 

k

y _n

g 0.5

Проверка:




 2



^ cos (2 x) dx 0.5

_



4

Пример 2. Вычисление интеграла от заданной функции f(x)на отрезке

a; b

при делении отрезка на 30 равных частей методом трапеций, с применением прикладного программного средства (MathCAD).

f(x) :

1 _;

x³  64

a:2;

b2;

n:30 _.

Решение: Задаем концы интервала интегрирования aи b.
х:= -2, -1.99999 .. 2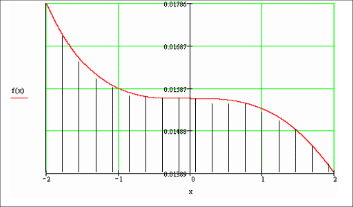




Рис.2

Площадь подынтегральной кривой, ограниченной прямыми х=-2, х=2, осью ОХ

и функцией

f(x) :
2

1 _;

x³  64

2 ₁

будет равна _f( x)dx_{ 3} dx

x  64

2 2