Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени. Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24

• Название: Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24
• Дата: 23.03.2022
• Размер: 1.58 Mb.
• Имя файла: Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени.docx
• Тип: Лабораторная работа; #410752
• страница: 7 из 15

Пример 4. Вычисление интеграла от заданной функции f(x)на отрезке
a; b

при делении отрезка на 30 равных частей методомсреднихпрямоугольников,

с применением прикладного программного средства (MathCAD).

f (x) :

1 _;

x³  64
a:2 ;
b:2;

n:30 _.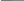

Решение: Программноерешениеметодасреднихпрямоугольников:

Integr

( a  b  n  char ) 

hf 

b  a n

for

i  0  n

xf_i  a  hf i

 

n 1
 ⁿ 

if char "left"  hf _

^f^{xf t} ^{ hf }_ ^f^{xf t}

 

Находим сумму левых прямоугольников:

Integr(a, b, n, "left") 0.062907481

t 0

 ^{t 1} 

Находим сумму правых прямоугольников:

Integr(a, b, n, "right") 0.062378381

Находим результат интегрирования:

_{Integr_ sr:}(Integr(a, b, n, "left")  Integr(a, b, n, "right")

2

Integr_ sr0.062643
Ответ:S=0.062643

"Ручное" решение метода средних прямоугольников: i:=0..n;

_h:(b a)_;

n

h0.133333

x_i :a  h i ; y_i: f(x_i).

Находим сумму левых прямоугольников:
n1

S1:h_ y_k ,

k0

S1 0.062907 ^.

Находим сумму правых прямоугольников:

n

S2 :h_y_k,

k1

S2 0.062378 _.

	0
0	0.017857
1	0.017393
2	0.017009
3	0.016693
4	0.016435
5	0.016226
6	0.016059
7	0.015927
8	0.015826
9	0.015751
10	0.015698
11	0.015662
12	0.015641
13	0.01563
14	0.015626
15	0.015625
16	0.015624
17	0.01562
18	0.015609
19	0.015588
20	0.015553
21	0.015501
22	0.015429
23	0.015334
24	0.015214
25	0.015067
26	0.014891
27	0.014685
28	0.014449
29	0.014184
30	0.013889

	0
0	-2
1	-1.867
2	-1.733
3	-1.6
4	-1.467
5	-1.333
6	-1.2
7	-1.067
8	-0.933
9	-0.8
10	-0.667
11	-0.533
12	-0.4
13	-0.267
14	-0.133
15	0
16	0.133
17	0.267
18	0.4
19	0.533
20	0.667
21	0.8
22	0.933
23	1.067
24	1.2
25	1.333
26	1.467
27	1.6
28	1.733
29	1.867
30	2

_{x } y 


Находим результат интегрирования:

_S:(S1 S2) _;

2

S0.06264

Упражнение 1.

Вычислить:

1. 
   с помощью «ручной» расчетной таблицы и калькулятора;
   
2. 
   с применением программного табличного редактора Ms’Excel;
   
3. 
   с применением прикладного программного средства MathCAD.
   

Вычислить интеграл от заданной функции f(x)на отрезке

а; b

при делении

отрезка на 30 равных частей тремя методами: методом трапеций, методом Симпсона, методом средних прямоугольников.

Произвести оценку погрешности методов интегрирования и сравнить точность полученных результатов.

Исходные данные для выполнения лабораторных работ № 3, 4 берутся из таблицы 5. Отрезок интегрирования разбивается на 30 равных частей и производится ручное вычисление интеграла по формулам трапеций, прямоугольников, Симпсона. Для расчетов по формулам трапеций рекомендуется составить единую таблицу значений подынтегральной функции по схеме:

X	yi/2(i=0,30)	yi(i=1,2,3,….,29)	2yi(i= 1,3,5,7,...,29)

По каждому из трех столбцов таблицы находятся суммы соответствующих значений подынтегральной функции (при этом по столбцу y_iдля формулы трапеций находится сумма всех элементов столбца, а для Симпсона – только с четными индексами). Вычисления ведутся с максимально возможной точностью вычислительного прибора или инструмента.
Для оценки точности методов использовать оценочные формулы:

1. 
   для метода трапеций:
   

eM
, где ^М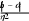

12

 max f

a,b

^{( x)} .

2. 
   для метода Симпсона: ^eM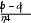
   

180
, где ^M

 max f

a, b
^{IV( x)} .

Их применение предполагает соответственно второй и четвертой производной

подынтегральной функции на отрезке а;b. В случае, когда исследование

общими методами оказывается слишком затруднительным, можно воспользоваться табулированием указанных производных на отрезке с подходящим шагом на ПК (по необходимости такая таблица может локально

уплотняться на экстремальных участках отрезка а; b).

Проанализировать полученные результаты, сделать вывод.

Таблица 5

Вариант	F(x)	а	b
1.	0,37esin x	0	1
2.	0,5+xlgx	1	2
3.	(x+1,9)sin(x/3)	1	2
4.	1 ln(x 2) x	2	3
5.	3cos x 2x 1,7	0	1
6.	(2x+0,6)cos(x/2)	1	2
7.	2,6x2lnx	1.2	2.2
8.	(x2+1)sin(x-0,5)	0.5	1.5
9.	x2cos(x/4)	2	3
10.	sin(0,2x 3) x2  1	3	4
11.	3x+lnx	1	2
12.	2 4xex	-1	0
13.	3x2+tqx	-0.5	0.5
14.	3x2  sin xx2	0	1
15.	3xecosx	0.2	1.2
16.	x2tqx 2	1.5	2.5
17.	xe x	0.1	1.1
18.	3,1xln2x	1.4	2.4
19.	(x-0,8)lnx 2	2.3	3.3
20.	(x-3,1)etqx	0	1
21.	y x2x 5	-1	1
22.	y 1 (2x 7 )(3x 4 )	0	4
23.	y x (1  2x)2	1	5

24.	y x 4  3x	1	5
25.	y 1 3x2  4x 2	-2	2
26.	y x (2x 7)(3x 4)	-1	1
27.	x2 y x2  16	0	2
28.	y 1 x3  64	-2	2
29.	2 y x x3  27	-2	2
30.	y x (1  2x)2	1	3

Задания для самостоятельной работы
Задание 1. Вычисления определенных интегралов (таблица 6) и неопределенных интегралов (таблица 7) от функций; составить программы для вычисления определенного интеграла и неопределенных интегралов.
Таблица 6

№вар.	Вычислить интеграл f(x)
1.	2 (x2  1) sin(x 0.5)dx 1
2.	5 (x x2  1)dx; 5
3.	4 (3x 2)2 (2x 2)dx; 0
4.	1 ex1  ex 0
5.	3 x3  1 (1  x2 )3
6.	1 x   (x 3)2dx 0 2
7.	1 x  2 dx 0 1  x

8.	2 2x 3cos(x)  7 sin(2.5x) 1
9.	10 sin(6x)  10 cos(3x)dx 0
10.	4 (5x 2)2 (6x 2)dx; 1
11.	3 ((2x x3 )  cos x)dx 0
12.	1 4 2x3  dx 1  x2 0
13.	2 x(1  ex) x exdx 0
14.	p 3 (sin x x)dx; p 6
15.	2 (2  x)  xexdx 1
16.	1 0,37esin xdx 0
17.	1 3cos x 2x 1,7 dx 0
18.	0 4xex2 dx 1
19.	1.1  xexdx 0.1
20.	4 1  (2x 7 )(3x 4 )dx 0
21.	5 x 4  3xdx 1
22.	1 x (2x 7)(3x 4) dx 1
23.	2 (x 1,9) sin( x3)dx 2
24.	3 x (1  2x)2 dx 1
25.	1 sin(2x2  1)dx 0

26.	2 x2 x3  27 dx 2
27.	3  1  cos2 xdx 0
28.	2 x (x 1,9) sin( 3)dx 1
29.	2 1 3x2  4x 2 dx 2
30.	2 x2 x2  16 dx 0

Таблица 7

№вар.	Вычислить интеграл f(x)
1.	 sin(x) 1  cos(x)  sin(x)
2.	 1 dx sin 3 (x) cos(x)
3.	1 ln(x 2)dxx
4.	2,6x2 ln xdx
5.	x2 cos( x)dx 4
6.	(3x2  tgx)dx
7.	 21 dx (6  7x)2
8.	 15 dx (2  x)3
9.	 3 dx (15x 9)3
10.	exsin(x2 )dx
11.	 12 dx (4x 9)2
12.	 4 dx (1  8x)2
13.	 1  cos(x) 1  cos(x)  sin(x)

14.	 1 dxx(1  x2 )
15.	tgxdx
16.	(x2  1) sin(x  0,5)dx
17.	(3x ln x)dx
18.	xe xdx
19.	 8 dx (3x 4)2
20.	 9 dx (5x 7)2
21.	1  e2x dx 5
22.	 17 dx (1  3x)3
23.	 5 dx (4x 3)3
24.	3x sin xdx x2
25.	 21 dx (6  7x)2
26.	 15 dx (2  x)3
27.	 3 dx (15x 9)3
28.	exsin(x2 )dx
29.	 12 dx (4x 9)2
30.	 4 dx (1  8x)2