Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени. Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24

• Название: Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24
• Дата: 23.03.2022
• Размер: 1.58 Mb.
• Имя файла: Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени.docx
• Тип: Лабораторная работа; #410752
• страница: 6 из 15

способ:

Найдем шаг:
_h:(b a) _;

n

h0.133333

Найдем точность метода трапеций:

1. 
   находим вторую производную
   

f(x)
_d2

pr2(x) : _dx2
f(x)

2. 
   находим максимальное значение второй производной на отрезке
   

a; b:

max pr2:=max(pr2(a), pr2(b)) max pr2=0.005466

3. 
   точность ^{emax L}
   

_h2

pr2(b a) 

12

0.00003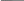

Программноерешениеметодатрапеций:

Trapec (a  b  n) 

hf 

b  a n

for

i  0 n

xf_i 

a  hf i

n 1

^f^xf₀ <sup>

f</sup>^xf_n ^

2 _

^f^xf_t

s  hf 
s

t 1

2

Находим значение интеграла:

Trapec(a, b, n) 0.06264

2. способ:

"Ручное"решениеметодатрапецийвпакетеMathCAD:

i:0 .. n; k:1.. (n1) ;

x_i:a hi y_i: f(x_i)

	0
0	-2.000
1	-1.867
2	-1.733
3	-1.600
4	-1.467
5	-1.333
6	-1.200
7	-1.067
8	-0.933
9	-0.800
10	-0.667
11	-0.533
12	-0.400
13	-0.267
14	-0.133
15	0.000
16	0.133
17	0.267
18	0.400
19	0.533
20	0.667
21	0.800
22	0.933
23	1.067
24	1.200
25	1.333
26	1.467
27	1.600
28	1.733
29	1.867
30	2.000

	0
0	0.01786
1	0.01739
2	0.01701
3	0.01669
4	0.01644
5	0.01623
6	0.01606
7	0.01593
8	0.01583
9	0.01575
10	0.01570
11	0.01566
12	0.01564
13	0.01563
14	0.01563
15	0.01563
16	0.01562
17	0.01562
18	0.01561
19	0.01559
20	0.01555
21	0.01550
22	0.01543
23	0.01533
24	0.01521
25	0.01507
26	0.01489
27	0.01469
28	0.01445
29	0.01418
30	0.01389

x  ^{y }

По формуле трапеций находим, что искомый интеграл будет равен:

 

s:0.5 h_y₀  _(2 y_k)  y_n; S:=0.06264

 k 

Ответ: S=0.06264

Пример 3. Вычисление интеграла от заданной функции f(x)на отрезке

a; b

при делении отрезка на 30 равных частей методом Симпсона, с применением прикладного программного средства (MathCAD).

f(x) :

1 _;

x³  64

a:2 ;

b:2;

n:30 _.

Решение:
_h:(b a)_;

n

h0.133333^.

Находим точность метода Симпсона:

1. 
   находим четвертую производную
   

f(x),

_d4

q(x) :_dx4

f (x) _;

2. 
   находим максимальное значение четвертой производной на отрезке
   

a; b:
max q:=max (q(a), q(b)) max q=0.015429

_h4

3. 
   точность e
   

max q(b a) 

180

0.0000001

ПрограммноерешениеметодаСимпсона:

Simpson(a b n) 

n 
hf 

n  1 if b  a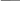

n

mod(n 2)  0

for

i  0 n ^

xf_i 



a  hf i

n n _

2 2

^{hf f}^xf  ^{ f}^xf  ^{ 4 }

_ ^f^xf

 ^{ 2 }

_ ^f^xf

_{ }

3. 
   0 n
   


iUneven 1

2iUneven1
iNeven 2

2iNeven 2



Simpson(a b n) 0.0626407

"Ручное"решениеметодаСимпсонавпакетеMathCAD:

i:0 .. n;

k:1, 3 .. (n1) ;

j:2 ,4 ..(n 2);

x_i:a hi y_i: f(x_i)

	0
0	-2.000
1	-1.867
2	-1.733
3	-1.600
4	-1.467
5	-1.333
6	-1.200
7	-1.067
8	-0.933
9	-0.800
10	-0.667
11	-0.533
12	-0.400
13	-0.267
14	-0.133
15	0.000
16	0.133
17	0.267
18	0.400
19	0.533
20	0.667
21	0.800
22	0.933
23	1.067
24	1.200
25	1.333
26	1.467
27	1.600
28	1.733
29	1.867
30	2.000

	0
0	0.0178571
1	0.0173926
2	0.0170090
3	0.0166934
4	0.0164352
5	0.0162260
6	0.0160586
7	0.0159270
8	0.0158260
9	0.0157510
10	0.0156977
11	0.0156621
12	0.0156406
13	0.0156296
14	0.0156256
15	0.0156250
16	0.0156244
17	0.0156204
18	0.0156094
19	0.0155881
20	0.0155530
21	0.0155010
22	0.0154290
23	0.0153342
24	0.0152142
25	0.0150670
26	0.0148909
27	0.0146852
28	0.0144493
29	0.0141835
30	0.0138889

_{x } y 

По формуле парабол (Симпсона) находим,

_h  

S :₃ y₀  _(4 y_k)  _(2 y_j)  y_n; S:=0.06264

_ _kj_

Ответ: S=0.06264