Курсовая работа по численным методам. ЧМ КР Медведев ТКС-20. Пояснительная записка к курсовой работе по дисциплине Численные методы
 Скачать 329.03 Kb.
|
|
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра «Автоматика и телекоммуникации» ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовой работе по дисциплине «Численные методы» Выполнил: студент группы СУА-20 Медведев А.В. Принял: ст. преподаватель кафедры АТ Долгих И.П. г. Донецк 2022 ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ Решить систему линейных уравнений, предварительно вычислить определитель, прямым методом с  ; уточнить полученное решение численным методом с  . 1) Метод Гаусса по схеме единственного деления; 2) Метод простой итерации.  2. Решить систему нелинейных уравнений графическим методом с или c  ; решить систему нелинейных уравнений с методом Ньютона, получив систему линейных уравнений и решив ее методом из первого раздела, а потом итерационным методом, указанным в задании. Сравнить между собой метод Ньютона и итерационный методы по количеству итераций, необходимых для нахождения корней с заданной точностью. 3. Решить дифференциальное уравнение ІІ порядка на отрезке в постановке задачи Коши с заданными начальными условиями. Начальные значения для метода Адамса рассчитать по методу Эйлера; краевой задачи с заданными граничными условиями. Принять  ; Задача Коши  [1,2;1,5]   М1 - Одношаговый метод Эйлера; M5 – Трёхшаговый метод Адамса Краевая задача –  
СОДЕРЖАНИЕ ВВЕДЕНИЕ Современная вычислительная техника требует познание основ численных методов (вычислительной математики) и использование этих умений на практике, которыми должен обладать каждый специалист технической направленности. Целью курсовой работы по дисциплине «Численные методы» является классификация теоретических познаний и фактических навыков, полученных при изучении дисциплины, решения систем линейных, нелинейных и дифференциальных уравнений 1 и 2 порядка. Предметом изучения является процесс и способы решения разных линейных систем уравнений, нелинейных систем уравнений и дифференциальных уравнений с максимально возможной точностью. В курсовой работе исследуем системы уравнений, чтобы изучить методы их решения. Для этого выберем методы решения в соответствии с вариантом и проведем оценку полученных результатов. Раздел первый содержит в себе прямой метод решения (метод Гаусса по схеме единственного деления) и численный метод (простой итерации) для решения систем линейных уравнений (СЛУ). Раздел второй представляет численные методы (метод Ньютона, метод Зейделя) и графический метод для решения систем нелинейных уравнений (СНУ). Раздел третий демонстрирует численные методы решения задачи Коши для дифференциальных уравнений II порядка. Применены 2 метода решения ДУ: Одношаговый метод Эйлера и трёхшаговый метод Адамса. Также приведен метод решения краевой задачи для дифференциальных уравнений II порядка. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ Постановка задачи Система  линейных уравнений с неизвестными имеет вид: (1.1)Совокупность коэффициентов запишем в виде матрицы  (1.2)Систему уравнений можно записать в матричном виде :  где  и  – вектор-столбец неизвестных и вектор-столбец правых частей: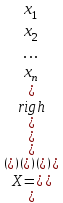 ,  .Совокупность чисел  ( вектор ), которые превращают систему в тождество называется решением этой системы, а сами числа  – ее корнями.Для существования единственного решения системы линейных уравнений необходимо и достаточно, чтобы определитель матрицы А не равнялся 0:  .1.2 Метод Гаусса по схеме единственного деления Метод Гаусса по схеме единственного деления состоит в следующем: удовлетворение на этапе прямого хода требования неравенства нулю коэффициентов  . В ином случае необходимо предварительно переставить уравнения системы.Прямой ход состоит в приведении матрицы А к верхнему треугольному виду путем последовательного исключения неизвестных из уравнений системы: При решении первого уравнения исключается х1 из второго и всех последующих уравнений, при решении второго – исключается из третьего и всех последующих и т.д., пока в левой части последнего уравнения не останется один член с неизвестным хn. Решим систему уравнений:  Выполним прямой ход. Первый шаг преобразований.Т.к. коэффициенты 1-го столбца неравны нулю, перестановка уравнений местами не требуется. Вычислим значения:  и  Для второго уравнения    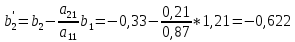 Для третьего уравнения:     Для четвертого уравнения:     Т.о. после первого шага преобразований СЛУ примет вид:  Второй шаг преобразований. Т.к. коэффициенты 2-го столбца неравны нулю, перестановка уравнений местами не требуется. Вычислим значения: Для третьего уравнения:    Для четвертого уравнения: 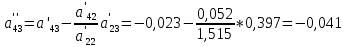   Т.о. после второго шага преобразований СЛУ примет вид:  Третий шаг преобразований. Т.к. коэффициенты 3-го столбца неравны нулю, перестановка уравнений местами не требуется. Вычислим значения: 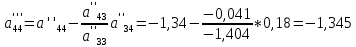  Т.о. после третьего шага преобразований СЛУ примет вид:  Матрица коэффициентов полученной СЛУ имеет треугольный вид. Выполним обратный ход:    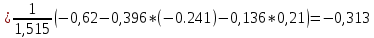   Теперь запишем результаты обратного хода с  : Выполним проверку полученного результата подстановкой в исходную СЛУ:  Абсолютные погрешности решения СЛУ составляют: Для первого уравнения – 0,0034; Для второго уравнения – 0,0098; Для третьего уравнения – 0,0061; Для четвертого уравнения – 0,0054. Таким образом корнями СЛУ с являются 1.3. Метод простой итерации Коэффициенты  должны удовлетворять условию (1.6). При этом хотя бы для одного уравнения неравенство должно выполняются строго. Преобразуем систему линейных уравнений, для этого разрешим i-ое уравнение системы относительно неизвестного  . (1.6) (1.7)В качестве начального (нулевого) приближения неизвестных xi(0),  выбираем:– значения, полученные путем решения системы прямым методом; – столбец свободных членов преобразованной системы,  ;– нулевые значения; – произвольные значения. Используя (1.8) последовательно выполняем итерации   (1.8)Первая итерация 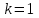 : 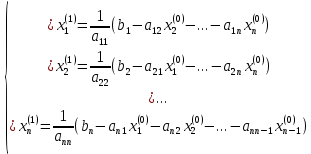Вторая итерация  :  Итерационный процесс продолжаем до момента, пока на k-ой итерации не выполнится критерий по абсолютным погрешностям:  (1.9)где  – заданная предельная абсолютная погрешность неизвестных.При выполнении условия (1.9) за искомое решение принимаем значения, вычисленные на последней k-ой итерации. Решим систему уравнений методом простой итерации с Δ=0,001: Проверим условие (1.6) для – первого уравнения:  ;–второго уравнения:  –третьего уравнения:  ;–четвертого уравнения:  .Условие (1.6) строго выполняется для каждого уравнения СЛУ. Преобразуем исходную СЛУ по (1.7).  В качестве нулевого приближения неизвестных xi(0),  выберем значения, полученные решением СЛУ Методом Гаусса прямым методом с : Используя (1.8) последовательно выполняем итерации  Первая итерация 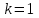:  Проверим условие (1.9) для: – первого уравнения:  ;–второго уравнения:  ;–третьего уравнения:  ;–четвертого уравнения:  .Условие (1.9) не выполняется, т.к.  > 0,001.Вторая итерация k=2: 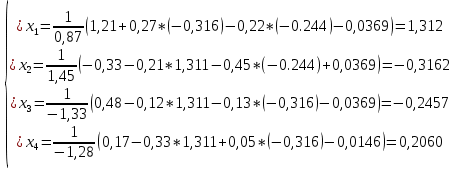 Проверим условие (1.9) для: – первого уравнения:  ;–второго уравнения:  ;–третьего уравнения: 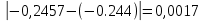 ;–четвертого уравнения:  .Условие (1.9) не выполняется, т.к.  >0,001.Третья итерация k=3:  Проверим условие (1.9) для: – первого уравнения:  ;–второго уравнения:  ;–третьего уравнения:  ;–четвертого уравнения:  .Условие (1.9) выполняется, т.к.  .Запишем результаты третьей итерации с требуемой : Выполним проверку полученного результата подстановкой в исходную СЛУ:  Абсолютные погрешности решения СЛУ составляют для первого уравнения 0,0003, для второго – 0,0005, для третьего – 0,0006, для четвертого – 0,0003 Таким образом корнями СЛУ с  являются 2. РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||