Курсовая работа по численным методам. ЧМ КР Медведев ТКС-20. Пояснительная записка к курсовой работе по дисциплине Численные методы
 Скачать 329.03 Kb. Скачать 329.03 Kb.
|
|
2.1 Постановка задачи Общий вид системы из n нелинейных уравнений с неизвестными х1, х2,…,хn 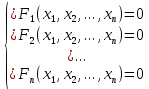 (2.1) (2.1)Для СНУ (7.1) не существует аналитических методов решения. В некоторых случаях систему можно решить непосредственно. Например, для системы из 2-х нелинейных уравнений с 2-мянеизвестными х1, х2 иногда удается выразить одно неизвестное через другое неизвестное и свести СНУ к решению одного нелинейного уравнения. 2.2 Графический метод Исходная система нелинейных уравнений имеет вид: 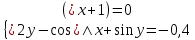 Преобразуем исходную СНУ к виду (2.1): 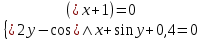 Построим графики функции 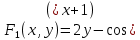 (Синий цвет в Приложение 1) и (Синий цвет в Приложение 1) и 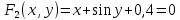 (Красный цвет в Приложении 1). С точностью (Красный цвет в Приложении 1). С точностью  . Определим координаты точки пересечения графиков (Приложение 1) : . Определим координаты точки пересечения графиков (Приложение 1) : 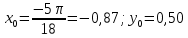 2.3 Метод Ньютона Решение системы (2.1) сводится к решению СНУ (1.1). Составляем матрицу Якоби 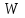 – матрицу из частных производных, вычисленных для функций – матрицу из частных производных, вычисленных для функций 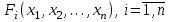 системы (2.1) по каждому неизвестному системы (2.1) по каждому неизвестному 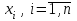 . .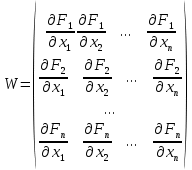 Выбираем 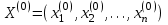 . .Последовательно выполняем итерации  , на каждой из которых составляем и решаем систему из n линейных уравнений относительно погрешностей , на каждой из которых составляем и решаем систему из n линейных уравнений относительно погрешностей 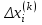 , , 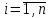 неизвестных неизвестных 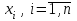 . .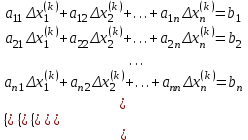 (2.7) (2.7)где 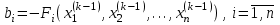 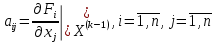 Полученные значения 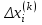 используем для уточнения значения неизвестных используем для уточнения значения неизвестных 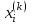 на k-ой итерации: на k-ой итерации: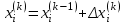 , , 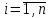 Продолжаем итерационный процесс до тех пор, пока на k-ой итерации выполнится условие: 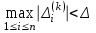 (2.8) где (2.8) где 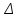 – заданная предельная абсолютная погрешность неизвестных. – заданная предельная абсолютная погрешность неизвестных.Решаем систему нелинейных уравнений с точностью до 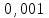 методом Ньютона. методом Ньютона. Преобразуем СНУ к виду (2.1): 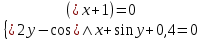 Составим матрицу Якоби 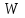 : :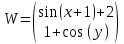 В качестве нулевого приближения неизвестных xиyвыберем значения, полученные решением системы графическим методом с  в разделе 2.2 (Приложение 1): в разделе 2.2 (Приложение 1): 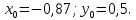 Используя (2.2) последовательно выполняем итерации  , на каждой из которых составляем и решаем систему из двух линейных уравнений относительно погрешностей , на каждой из которых составляем и решаем систему из двух линейных уравнений относительно погрешностей 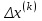 , , 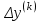 неизвестных неизвестных 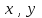 . .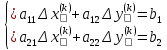 , где , где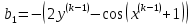 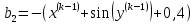 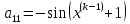 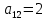 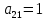 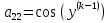 Первая итерация k=1: 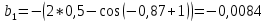 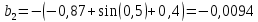 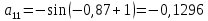 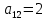 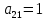 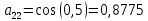 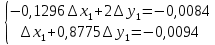 В результате решения СЛУ прямым методом находим значения погрешностей 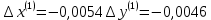 , и вычисляем первое приближение неизвестных , и вычисляем первое приближение неизвестных 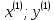 : :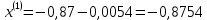 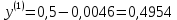 Условие (2.3) не выполняется т.к. | 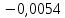 |= |=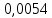 >0,001 >0,001Вторая итерация k=2: 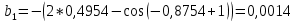 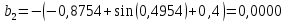 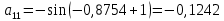 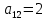 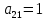 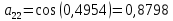 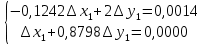 В результате решения СЛУ Методом Гаусса прямым ходом находим значения погрешностей 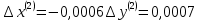 , и вычисляем первое приближение неизвестных , и вычисляем первое приближение неизвестных 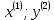 : :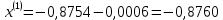 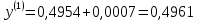 Условие (2.3) выполняется. Запишем результаты с требуемой 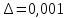 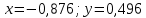 Выполним проверку полученного результата подстановкой в исходную СНУ: 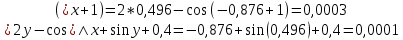 Абсолютные погрешности СНУ составляют: Для первого уравнения 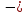 0,0003 0,0003 Для второго уравнения 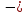 0,0001 0,0001 В обоих случаях погрешности являются меньшими заданного значения 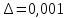 . Таким образом корнями СНУ с . Таким образом корнями СНУ с 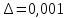 являются: являются: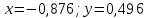 Решение получено за 2 итерации 2.4 Метод Зейделя Определим 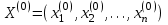 графически или аналитически. Преобразование СНУ (2.1) к виду (2.2) и проверка условия (2.3)-(2.4) аналогичны соответствующим действиям метода итераций. графически или аналитически. Преобразование СНУ (2.1) к виду (2.2) и проверка условия (2.3)-(2.4) аналогичны соответствующим действиям метода итераций. Используя (2.6), последовательно выполняем итерации  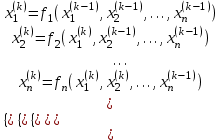 (2.6) (2.6)Итерационный процесс продолжают до тех пор, пока на k-ой итерации выполнится критерий (1.9). При выполнении условия (1.9) за искомое решения принимаем значения, вычисленные на последней k-ой итерации. Решаем систему нелинейных уравнений с точностью до 0,001 методом Зейделя: 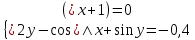 Для решения системы представим ее в виде (2.2): 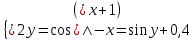 В качестве нулевого приближения неизвестных xиyвыберем значения, полученные решением СНУ графическим методом с  в разделе 2.2: в разделе 2.2: 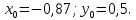 Первая итерация: 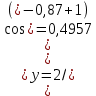 Проверим условие (1.9) для: – первого уравнения: 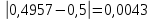 ; ;– второго уравнения: 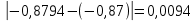 ; ;Условие (1.9) не выполняется, т.к.  . .Вторая итерация  : :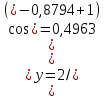 Проверим условие (1.9) для: – первого уравнения: 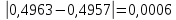 ; ;– второго уравнения: 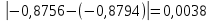 ; ;Условие (1.9) не выполняется, т.к. 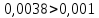 . .Третья итерация 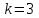 : :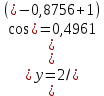 Проверим условие (1.9) для: – первого уравнения: 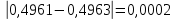 ; ;– второго уравнения: 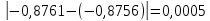 ; ;Условие (1.9) выполняется, т.к.  . .Запишем результаты третьей итерации с требуемой  : :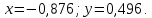 Выполним проверку полученного результата подстановкой в исходную СНУ: 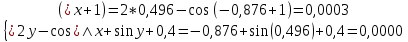 Абсолютные погрешности решения СНУ составляют для первого уравнения 0,0003, для второго – 0,0000 и являются меньшими заданного значения  . Таким образом корнями СНУ с . Таким образом корнями СНУ с  являются являются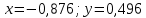 3. РЕШЕНИЕ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 3.1 Постановка задачи Система из  дифференциальных уравнений первого порядка, разрешенных относительно производных, имеет вид: дифференциальных уравнений первого порядка, разрешенных относительно производных, имеет вид: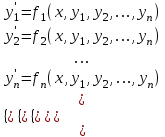 (3.1) (3.1)где 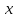 – независимая переменная. – независимая переменная.Решением СДУ (3.1) называется любая совокупность функций 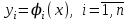 , которая после подстановки в (3.1), обращает ее в тождество. , которая после подстановки в (3.1), обращает ее в тождество.Общее решение системы (3.1) 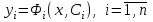 , где , где 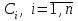 – произвольные постоянные. – произвольные постоянные.Частное решение системы получают из общего при определенных значениях произвольных постоянных, которые находят при наличии дополнительных условий. Если эти условия заданы в одной точке, получим задачу Коши. Одношаговые и многошаговые методы решения задачи Коши для дифференциальных уравнений первого порядка могут быть использованы и для решения задачи Коши СДУ. К решению СДУ сводится задача Коши для дифференциальных уравнений высших порядков. Рассмотрим ДУ второго порядка 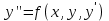 , где х – независимая переменная, с начальными условиями , где х – независимая переменная, с начальными условиями 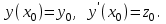 Введем вторую неизвестную функцию 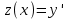 и получим систему из двух дифференциальных уравнений первого порядка, разрешенных относительно производных: и получим систему из двух дифференциальных уравнений первого порядка, разрешенных относительно производных: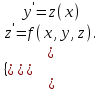 (3.2) (3.2)с начальными условиями 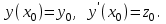 3.2 Одношаговый метод Эйлера Рассмотрим систему двух дифференциальных уравнений, где где х – независимая переменная, с начальными условиями 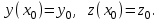 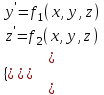 (3.3) (3.3)Формулы Эйлера решения СДУ (3.3): 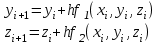 (3.4) (3.4)где 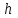 – шаг переменной – шаг переменной 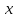 , , 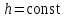 . .Решим обыкновенное дифференциальное уравнение второго порядка в поставленной задаче Коши с начальными условиями: Задача Коши  [1,2;1,5] [1,2;1,5] 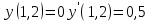 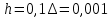 Представим дифференциальное второго порядка в постановке задачи Коши в виде системы двух дифференциальных первого порядка. Приведем исходное дифференциальное уравнение к виду 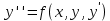 : :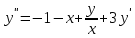 Введем вторую неизвестную функцию 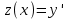 и получим по (3.2): и получим по (3.2):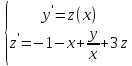 С начальными условиями 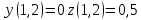 Разбив отрезок [1,2;1,5] на части с шагом 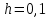 получим четыре узловые точки с абсциссами получим четыре узловые точки с абсциссами 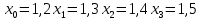 . . Точка 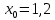 – начальная точка, тогда – начальная точка, тогда 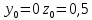 согласно исходным условиям. согласно исходным условиям.Найдем 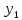 и и 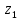 для для 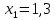 по (3.4): по (3.4):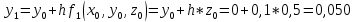 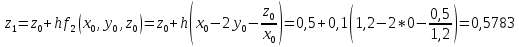 Найдем 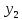 и и 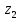 для для 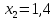 по (3.4): по (3.4):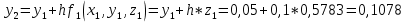 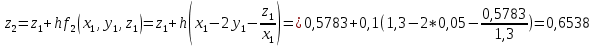 Найдем 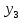 и и 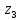 для для 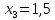 по (3.4): по (3.4):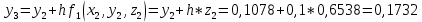 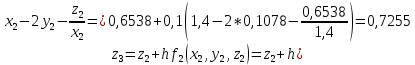 Ответ представим с 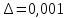 в виде таблицы в виде таблицыТаблица 1 – Результат расчетов одношаговым методом Эйлера
|
