Курсовая работа по численным методам. ЧМ КР Медведев ТКС-20. Пояснительная записка к курсовой работе по дисциплине Численные методы
 Скачать 329.03 Kb. Скачать 329.03 Kb.
|
|
3.3 Трёхшаговый метод Адамса Для использования многошаговых ( 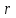 -шаговых) методов, необходимо сначала любым одношаговым методом вычислить решение на -шаговых) методов, необходимо сначала любым одношаговым методом вычислить решение на 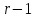 предыдущих шагах (в точках предыдущих шагах (в точках 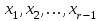 ). ).Формулы трёхшагового метода Адамса решения СДУ (3.3): 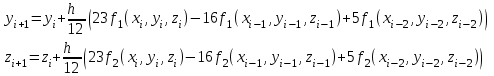 (3.8) (3.8)Решим дифференциальное уравнение второго порядка из пункта 3.2 Представим дифференциальное второго порядка в постановке задачи Коши в виде системы двух дифференциальных уравнений первого порядка 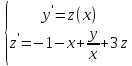 С начальными условиями 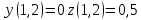 Разбив отрезок [1,2;1,5] на части с шагом 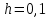 , получим четыре узловые точки с абсциссами , получим четыре узловые точки с абсциссами 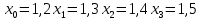 Т.к. начальной точкой является точка 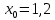 , то , то 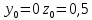 согласно исходным условиям. согласно исходным условиям.Решением в точке 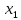 будут значения будут значения 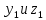 полученные с помощью Одношагового метода Эйлера в пункте 3.2 полученные с помощью Одношагового метода Эйлера в пункте 3.2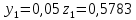 Решением в точке 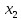 будут значения будут значения 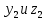 полученные с помощью Одношагового метода Эйлера в пункте 3.3: полученные с помощью Одношагового метода Эйлера в пункте 3.3: 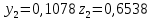 Найдем 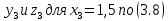 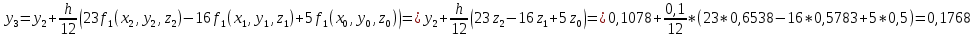 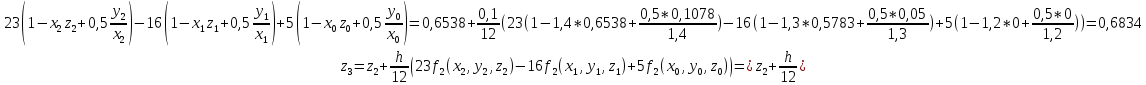 Ответ представим с 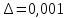 в виде таблицы в виде таблицыТаблица 2 - Результат расчетов Трёхшагового метода Адамса
3.4 Решение Краевой задачи Для дифференциального уравнения второго порядка 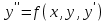 (3.6) (3.6)Краевая задача заключается в поиске функции 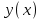 на отрезке на отрезке 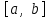 , удовлетворяющей на концах отрезка условиям, которые заданы в частном виде: , удовлетворяющей на концах отрезка условиям, которые заданы в частном виде: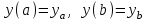 (3.7) (3.7)или в общем виде: 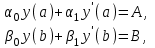 (3.8) (3.8)где 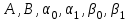 – некоторые постоянные величины. – некоторые постоянные величины.Рассмотрим метод конечных разностей, т.к. он позволяет свести решение краевой задачи для дифференциального уравнения к решению системы алгебраических уравнений относительно значений функции на заданном множестве точек. Это достигается путем замены производных, входящих в ДУ, их конечно-разностными аппроксимациями. Разобьем отрезок [a,b] на 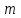 равных отрезков длиной h точками xi+1=xi+h , равных отрезков длиной h точками xi+1=xi+h , 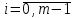 , где x0=aиxm=b. Точки , где x0=aиxm=b. Точки 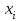 называют узлами сетки, называют узлами сетки, 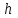 – шагом сетки, точки – шагом сетки, точки 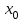 и и 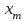 – граничными узлами, а – граничными узлами, а 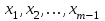 – внутренними узлами. – внутренними узлами.Решение краевой задачи заменим вычислением значений сеточной функции 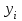 в узловых точках в узловых точках 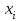 . Для этого запишем уравнение (3.6) для внутренних узлов: . Для этого запишем уравнение (3.6) для внутренних узлов: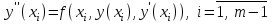 . (3.9) . (3.9)Заменим производные, входящие в эти соотношения их конечно-разностными аппроксимациями: 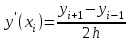 , , 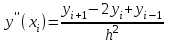 Подставляя эти выражения в (3.9), получим систему разностных уравнений, представляющей собой систему из 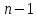 алгебраического уравнения относительно значений сеточной функции алгебраического уравнения относительно значений сеточной функции 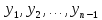 . значение . значение 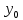 и и 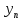 , входящих в эту систему, берут из граничных условий: , входящих в эту систему, берут из граничных условий: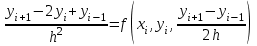 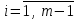 (3.10) (3.10)Если граничные условия заданы в общем виде (3.8), то их необходимо представить в разностном виде путем аппроксимации производных 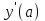 и и 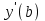 конечно-разностными соотношениями: конечно-разностными соотношениями: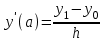 , , 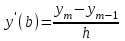 Т.о. граничные условия (3.9) примут вид: 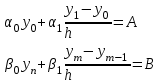 (3.11) (3.11)Система (3.10), дополненная при необходимости уравнениями (3.11), является системой из 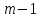 (или (или 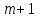 ) линейных или нелинейных уравнений, относительно значений сеточной функции ) линейных или нелинейных уравнений, относительно значений сеточной функции 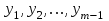 (или (или 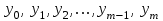 ). ). Матрица коэффициентов полученной СЛУ является трехдиагональной и может быть решена методом прогонки. Запишем трехдиагональную систему из n линейных уравнений в виде: 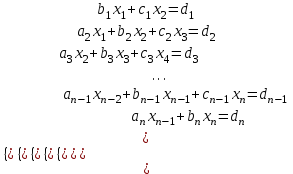 где 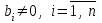 . .Метод прогонки состоит из этапов: прямой прогонки и обратной прогонки. На этапе прямой прогонки выражают из i-го уравнения неизвестное 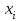 через через 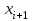 с помощью прогоночных коэффициентов: с помощью прогоночных коэффициентов: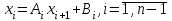 (3.12) (3.12)Из первого уравнения 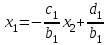 . .Поскольку 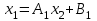 , следовательно: , следовательно: 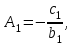 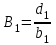 . .Из второго уравнения:  , ,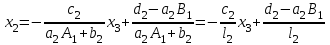 . .Поскольку 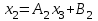 , следовательно , следовательно 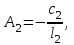 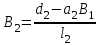 , , где 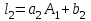 . .Для 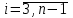 : : 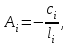 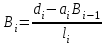 , , 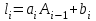 . .Обратная прогонка начинается с вычисления 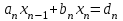 , ,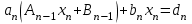 , ,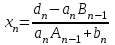 . .Далее вычисляют 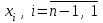 по формуле (3.15) и формулам прогоночных коэффициентов. по формуле (3.15) и формулам прогоночных коэффициентов.Решим с 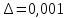 ДУ второго порядка ДУ второго порядка  в постановке краевой задачи методом конечных разностей на отрезке [1,2;1,5] c шагом в постановке краевой задачи методом конечных разностей на отрезке [1,2;1,5] c шагом 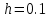 и граничными условиями: и граничными условиями:   Разбив отрезок [1,2 1,5] на части с шагом 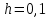 получим четыре узловые точки с абсциссами получим четыре узловые точки с абсциссами 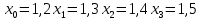 Две точки 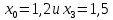 являются граничными, а остальные две – внутренними являются граничными, а остальные две – внутренними Исходное ДУ второго порядка во внутренних точках заменим конечно-разностными уравнениями по (3.10): 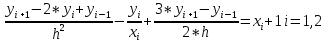 Из первого граничного условия, заданного в общем виде (3.11), составим конечно-разностное уравнение в граничной точке 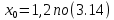 . . Из второго граничного условия, заданного в частном виде по (3.10), запишем значение 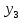 в граничной точке в граничной точке 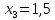 : :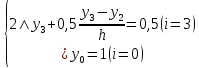 Таким образом, исходная задача сводится к решению системы уравнений 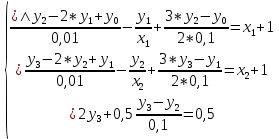 Решим полученную СЛУ методом прогонки. Из первого уравнения выразим 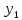 : :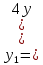 )/3 )/3Подставим выражение для 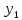 во второе уравнение и выразим из него во второе уравнение и выразим из него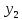 : :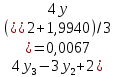 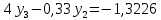 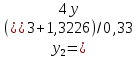 Подставим выражение для 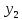 в третье уравнение и выразим из него в третье уравнение и выразим из него 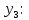 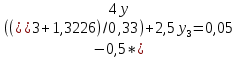 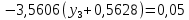 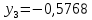 Вычислив значение 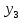 = =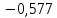 , вычислим далее , вычислим далее 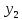 == ==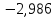 , из второго уравнения и , из второго уравнения и 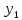 = =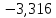 из первого уравнения. из первого уравнения.Ответ представим с  в виде таблицы. в виде таблицы.Таблица 3 - Результат решение Краевой задачи
ЗАКЛЮЧЕНИЕ В ходе выполнения курсовой работы исследованы методы решения систем линейных, нелинейных, дифференциальных уравнений. В первом разделе была решена система линейных уравнений с заданной точностью методом Гаусса по схеме единственного деления, в ходе которого найдены корни СЛУ, а так же получена абсолютная погрешность, а именно для первого уравнения – 0,0034, для второго – 0,0098, для третьего – 0,0061, для четвертого – 0,0054. После уточнено с заданной точностью полученное решение методом простой итерации, погрешностью которого не превышала 0,001. Во втором разделе исследована система из двух нелинейных уравнений. В ходе решения задействованы три метода: графический метод, метод Ньютона и итерационный метод Зейделя. Можно заключить что итерационный метод Зейделя является более точным, по сравнению с Методом Ньютона. В третьем разделе решено дифференциальное уравнение ІІ порядка на отрезке в постановке задачи Коши одношаговым методом Эйлера и методом трехшагового Адамса, а также в постановке краевой задачи с заданными графическими условиями. Можно констатировать РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА 1. Демидович Б.П, Марон И.А. Основы вычислительной математики. 3-е изд., испр. – М.: Наука, 1966. – 664 стр. 2. Краскевич В.Е., Зеленский К.Х., Гречко В.И. Численные методы инженерных исследований. – Киев: Высшая шк., 1986. – 263 стр. 3. Боглаев Ю.П. Вычислительная математика и программирование – М.: Высш. шк., 1990. – 544 стр. 4. Копченова Н.В., Марон И.В. Вычислительная математика в примерах и задачах. – М.: Наука, 1972. – 512с. 5. Самарский А.А., Гулин А.В. Численные методы: Учебное пособие для вузов. – М.: Наука. Гл. ред. физ-мат. лит., 1989. – 432 с. –C. 190 – 195. (Приложение 1) – Решение СНУ графическим методом. 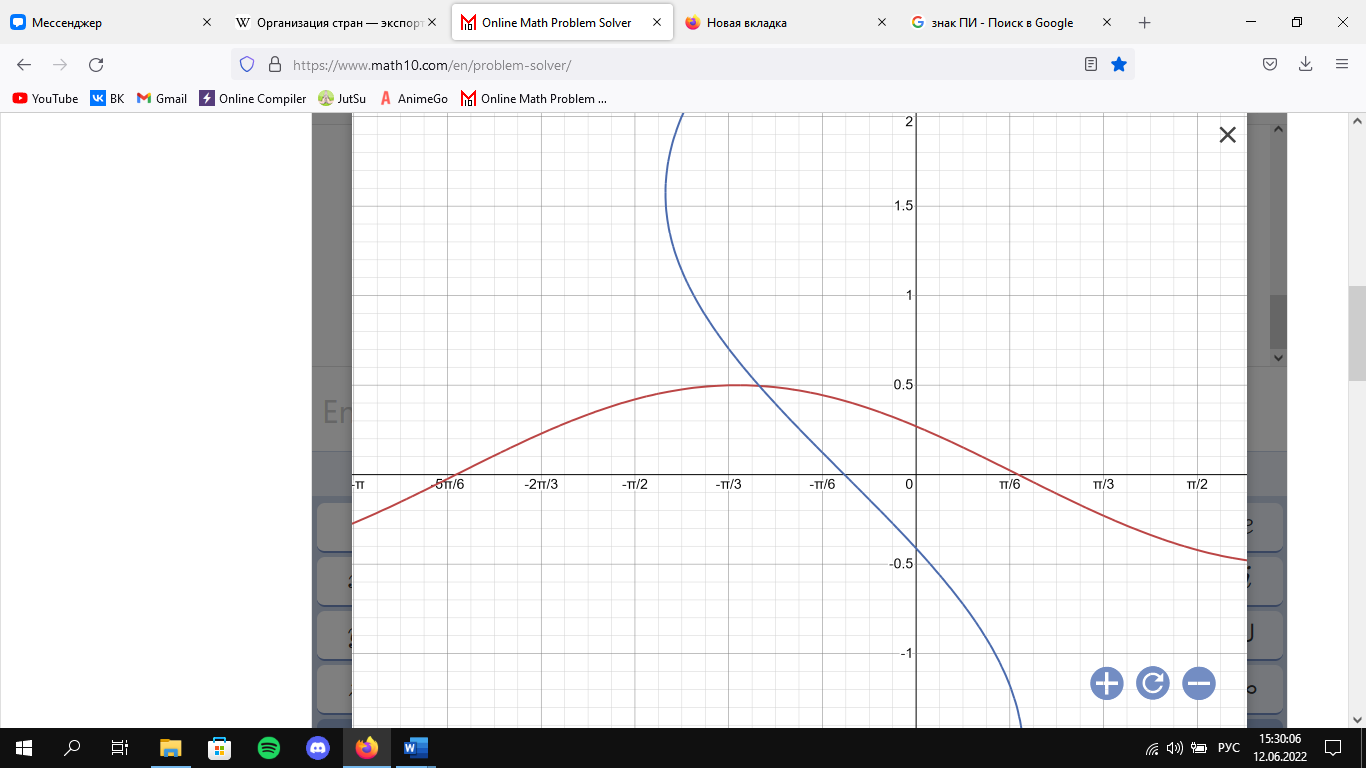 |