Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени. Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24

• Название: Лабораторная работа 2 14 Метод Ньютона (касательных). Метод итерации. 14 Лабораторные работы 3, 4 24
• Дата: 23.03.2022
• Размер: 1.58 Mb.
• Имя файла: Амиров_Д_Ф_«Численные_методы»_Методические_указания_по_выполнени.docx
• Тип: Лабораторная работа; #410752
• страница: 11 из 15

Пример 3. Решение СЛАУ методом простой итерации.

Дана СЛАУ:

1.2 x₁ 
0.22 x₂  0.1 x₃ 
0.1 x₄  0.1 x₅ 20

0.1 x₁  1.3 x₂  0.03 x₃  0.1 x₄  0.2 x₅ 3

0.15 x₁  0.1 x₂  0.8 x₃ 

0.1 x₄ 

0.1 x₅

3.9

0.5 x₁  0.1 x₂  0.28 x₃  0.94 x₄  0.1 x₅ 5

0.2 x₁  0.3 x₂  0.2 x₃  0.1 x₄  0.93 x₅ 9

Проверка условия сходимости:

0.22

0.1

0.15

0.5

0.2

 0.1 

 0.03 

 0.1 

 0.1 

 0.3 

0.1 

0.1 

0.1 

0.28 

0.2 

0.1

0.2

0.1

0.1

0.1

 1.2

 1.3

 0.8

 0.94

 0.93

Условие сходимости выполняется. Задаем коэффициенты а_{i, j} :

_1.2

0.22

0.1

0.1

0.1 _

_ 0.1

1.3

0.03

0.1

0.2 _

A  _ 0.15

^ 0.5

0.1

0.1

0.8

0.28

0.1

0.94

0.1 _

0.1 ^

_0.2

0.3

0.2

0.1

0.93 _

Задаем свободные коэффициенты b_i :

_ 20 _

 ³ 

B  _3.9 _

 ₅ 

 ⁹ 

Заданная точность: e:0.001

i:0 .. 4 ;
AA_{i j} 

j:0 .. 4

^Ai j


^Ai i

BB_i 
B_i ^Ai  i

AA_{i i} 0

_ 0 0.183

0.083

0.083

0.083 _

_ 0.077 0

0.023

0.077

0.154 _

AA _ 0.187

^ 0.532

_0.215

0.125

0.106

0.323

0

0.298

0.215

0.125

0

0.108

0.125 _

0.106 ^

0 _

_16.667 <sub>

</sub> 2.308 _

BB  _ 4.875 _

^ 5.319 ^

_ 9.677 _
Определяем коэффициент сжатия:

1 normi(AA)

2 norm1(AA)

3 norme(AA)

1 1.043

2 1.011

3 0.88

Определяем критерий достижения заданной точности:

Для определения критерия достижения заданной точности выбираем

a3 0.88 , т.к. a3 1.

E:^e

(1  a3)

a3

E0.000136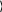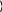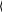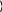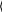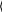

Вычисляем значение итерационной последовательности:

k:0 ..12 ;

x⁰ :BB;

_xk1

:BB  AAx^k

	0	1	2	3	4	5	6	7	8	9	10	11	12
0	-16.667	-16.320	-16.919	-16.740	-16.846	-16.849	-16.861	-16.859	-16.860	-16.860	-16.860	-16.860	-16.860
1	-2.308	-1.804	-1.995	-2.192	-2.238	-2.249	-2.247	-2.248	-2.248	-2.248	-2.248	-2.248	-2.248
2	-4.875	-9.586	-10.008	-9.854	-9.756	-9.758	-9.764	-9.767	-9.767	-9.767	-9.766	-9.766	-9.766
3	-5.319	-13.516	-11.471	-11.655	-11.531	-11.615	-11.612	-11.617	-11.615	-11.615	-11.615	-11.615	-11.615
4	-9.677	-4.872	-4.977	-4.477	-4.504	-4.475	-4.479	-4.475	-4.475	-4.475	-4.475	-4.475	-4.475

x 

^^x



k 1

^{  ( xk}



0

) ₀  ( x

k 1

) ₁  ( x^k

) ₁ 

^^x





k 1

^{  ( xk}



2

) ₂ 

 ( x

k 1

) ₃  ( x ^k

) ₃ 

^x



k 1

^{  ( xk ) 4} 4

	0
0	18.563135
1	3.361715
2	1.214966
3	0.401188
4	0.130606
5	0.025938
6	0.012797
7	0.002905
8	0.001141
9	0.000277
10	0.000119
11	0.000027
12	0.000011

Полученное десятое значение суммы модулей разности (0,000119) при

e0,000136 удовлетворяет условию. Значит, что 10 столбец значений х

является решением СЛАУ.

x₁ 16,860;

x₂ 2,248;

x₃ 9,766;

x₄ 11,615;

x₅ 4,475 _.

3




0
_x _k ₅






1

8
_x ^k^{ 6}








_x ^k^






2

1

3
_x ^k^

11

_x ^k^ _

4

13
15
16.92
k

trace 1

trace 2

trace 3

trace 4

trace 5

Зависимость x_i^(k) (i=0..4) от количества итераций (к)