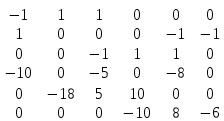Применение узловых и контурных матриц для определения токов в ветвях сложнозамкнутой электрической схемы с помощью законов Кирхг. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1 (с исправлениями). Применение узловых и контурных матриц для определения токов в ветвях сложнозамкнутой электрической схемы с помощью законов Кирхгофа Задание
 Скачать 367.05 Kb. Скачать 367.05 Kb.
|
|
Применение узловых и контурных матриц для определения токов в ветвях сложнозамкнутой электрической схемы с помощью законов Кирхгофа Задание Определить токи во всех ветвях электрической сложнозамкнутой сети (рис. 1) с помощью I и II-го законов Кирхгофа  Рис. 1 Исходные данные:
Решение (1 вариант): Первый закон Кирхгофа применяется к узлам схемы и выражает баланс токов в них (алгебраическая сумма токов в ветвях, сходящихся в узле, равна нулю). Второй закон Кирхгофа применяется к контурам электрической цепи и выражает баланс напряжения в них (алгебраическая сумма э.д.с. в замкнутом контуре равна алгебраической сумме падений напряжения во всех элементах этого контура). Общее количество уравнений для определения токов по законам Кирхгофа определяется количеством ветвей в схеме (в схеме рис. 1 количество ветвей, а значит и неизвестных токов, равно 6). Количество уравнений по первому закону Кирхгофа равно количеству независимых узлов в схеме (их на единицу меньше, чем число узлов в схеме, т.е. в схеме рис. 1 их будет 3) Количество уравнений по второму закону Кирхгофа равно количеству независимых контуров в схеме (их на единицу меньше, чем число узлов в схеме, т.е. в схеме рис. 1 их тоже будет 3). Независимый контур – это контур, имеющий хотя бы одну ветвь, не входящую в другие контуры. Итак, для рассматриваемой схемы всего уравнений будет 6: 3 – по первому закону Кирхгофа; 3 – по второму закону Кирхгофа. Уравнения по I закону Кирхгофа Приняв, направление входящих в узел токов положительным, а выходящих отрицательным, запишем уравнения для узлов схемы, представленной на рис. 1 (направления токов в ветвях схемы предварительно выбраны произвольно): для узла а:   для узла b:  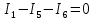 для узла с:   Уравнения по II закону Кирхгофа Правило: Если направление действия э.д.с. в контуре совпадает с направлением обхода контура, то в уравнении оно записывается со знаком плюс; если направление тока в ветви, содержащей сопротивление, совпадает с направлением обхода контура, то падение напряжения также принимается со знаком плюс. Задаем направление обхода контуров (рис. 2) и формируем уравнения 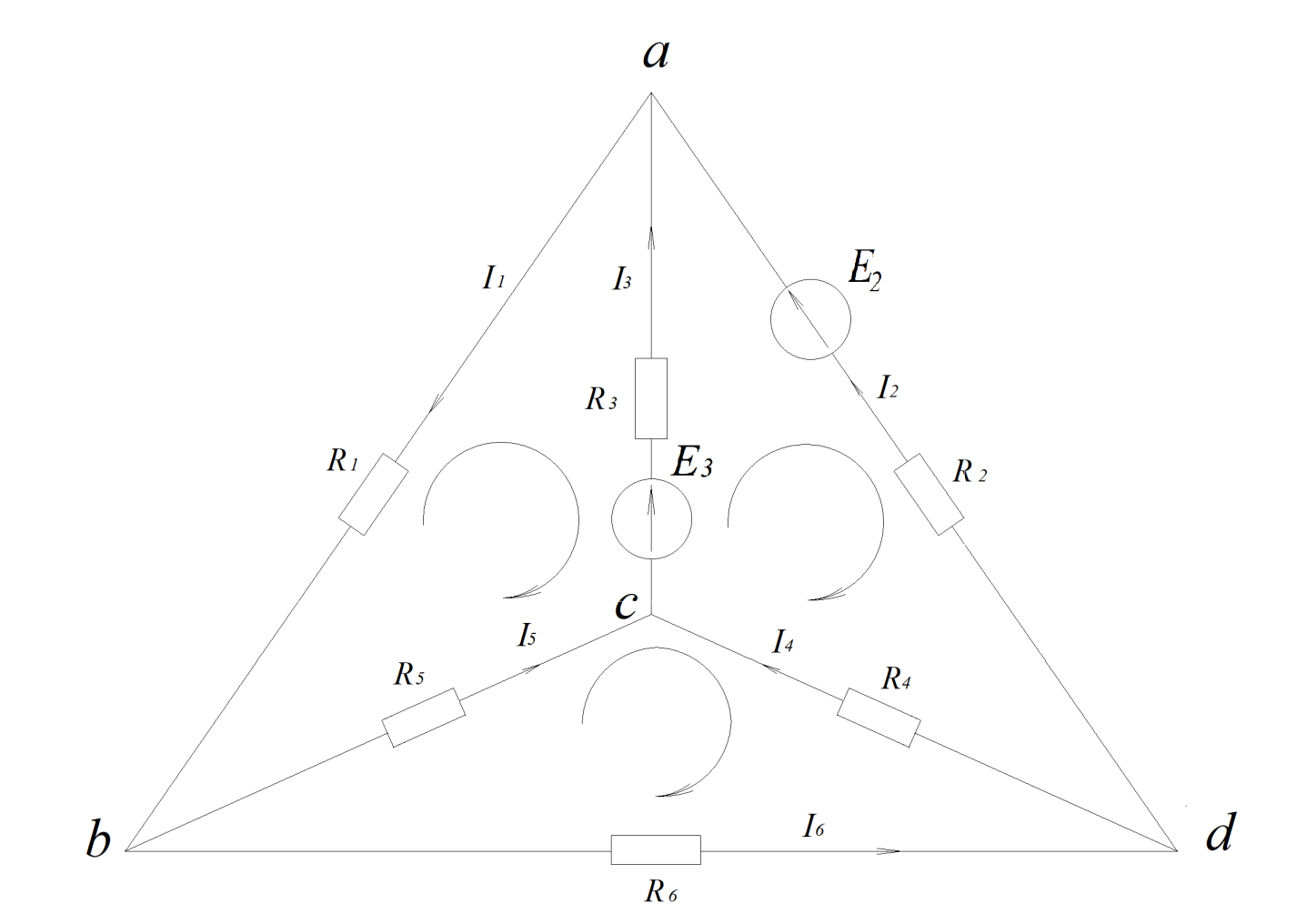 Рис. 2 Для контура abc:  ; ;для контура acd:  ; ;для контура bcd: 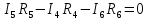 ; ;Объединяем все эти 6 уравнений в систему 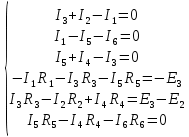 Составим матрицу соединений А и матрицу-столбец напряжений В на основании системы из приведенных выше уравнений в виде таблицы 1 Таблица 1
Примечания: R1=10 Ом; R2=18 Ом; R3=5 Ом; R4=10 Ом; R5 =8 Ом; R6=6 Ом; На основании данных табл. 1 можно составить узловую матрицу (матрицу соединений) – таблицу коэффициентов уравнений, составленных по первому закону Кирхгофа. Строки этой матрицы должны соответствовать узлам, а столбцы – ветвям схемы. Ее образуют первые три строки таблицы, т.е. уравнения для узлов схемы, и она будет выглядеть следующим образом 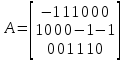 . .Уравнения по первому закону Кирхгофа записываются для (m-1) узлов. Данная матрица не содержит строку для узла d, и поэтому называется редуцированной, для нее сумма элементов каждого из столбцов не должна равняться нулю. Если ввести столбцовую матрицу токов ветвей 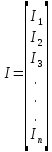 , ,то первый закон Кирхгофа в матричной форме запишется как 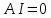 , ,где 0 – нулевая матрица-столбец. Произведя умножение матриц А и I, получим выражение
одним из решений которого является определение токов в узле а 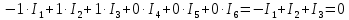 , ,которое говорит о том, что сумма токов в узле а равна нулю. Для всех узлов, кроме узла d
Контурная матрица (матрица контуров) – это таблица коэффициентов уравнений, составленных по второму закону Кирхгофа. Строки контурной матрицы В соответствуют контурам, а столбцы – ветвям схемы  Если ток ветви, вызывающий в сопротивлении ветви падение напряжения, направлен встречно направлению обхода контура, то в табл. 2 ставим -1; если ток ветви совпадает с направлением обхода контура, то +1; если ветвь с током не содержится в данном контуре, то – 0
Тогда матрица В запишется как  . .Математическая запись второго закона Кирхгофа выглядит следующим образом 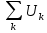 =0, =0,т.е. алгебраическая сумма напряжений на зажимах ветвей (элементов) контура равна нулю. Действительно, если просуммировать напряжения на ветвях некоторого контура 1-2-3-4-5, 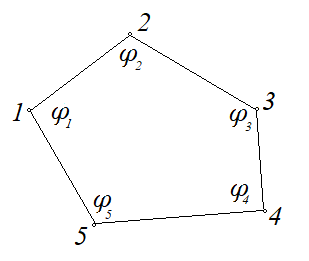 получим выражение 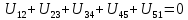 , а так как , а так как  , ,  , и т.д., то сумму падений напряжения на каждом из участков контура можно представить как сумму разностей потенциалов на этих участках , и т.д., то сумму падений напряжения на каждом из участков контура можно представить как сумму разностей потенциалов на этих участках + +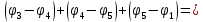 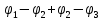 + + =0. =0. Сумма получается равной нулю, о чем и говорит II закон Кирхгофа. Элементы строки контурной матрицы [В] содержат сведения о ветвях, связанных с контурами цепей, и отражают направления напряжений (совпадающие с направлениями токов) на этих ветвях, а сумма произведений прямоугольной матрицы [В] на напряжения ветвей представляет собой второй закон Кирхгофа в матричной форме Применив данное рассуждение к составленной матрице В и введенной матрице-столбце напряжения ветвей U, 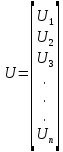 получим
Примечание: матрица-столбец напряжений ветвей [UB] учитывает наличие в ветвях источников напряжения, т.е. UBk = RkIk ± ЕВк, причем суммарную ЭДС ветви ЕВк записывают со знаками «плюс», если направления этой ЭДС и тока ветви не совпадают, и со знаком «минус» — в противоположном случае. В данной схеме ветви 2 и 3 содержат э.д.с., принимаемые со знаком «минус», так как согласно физическому смыслу напряжения и э.д.с. являются взаимоисключающими силами (подробно об этом здесь – http://new-idea.kulichki.net/pubfiles/150902145324.pdf). Запишем одно из контурных уравнений, например, для первого контура 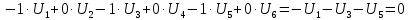 , ,что соответствует первому контурному уравнению составленной ранее системы  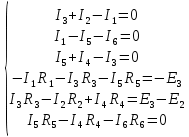
Для определения токов в ветвях необходимо сначала найти матрицу, обратную матрице А, а затем умножить ее на матрицу В методом Гаусса  , в Matcad или в онлайн-калькуляторе матриц, например https://ru.onlinemschool.com/math/assistance/matrix/, например, как показано в [1]. , в Matcad или в онлайн-калькуляторе матриц, например https://ru.onlinemschool.com/math/assistance/matrix/, например, как показано в [1]. Таким образом, токи в ветвях: I1= 1,512 А; I2= 0,09 А; I3= 1,422 А; I4= 0,451 А; I5= 0,971 А; I6= 0,542 А;
Применение матриц к расчету линейных электрических цепейhttps://studref.com/589942/tehnika/primenenie_matrits_raschetu_lineynyh_elektricheskih_tsepey3. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975. 752 с. с ил. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

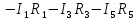

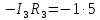




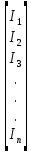 =0,
=0,
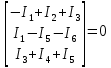
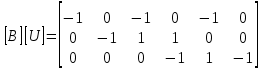 ·
·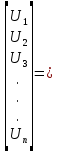
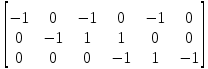 ·
· =0
=0