Главная страница
Навигация по странице:

  • Список используемой литературы.

    		•

    Контрольная. Примеры выполнения контр. Примеры выполнения Контрольной работы по метрологии, стандартизации и сертификации


    Скачать 1.13 Mb.
    НазваниеПримеры выполнения Контрольной работы по метрологии, стандартизации и сертификации
    АнкорКонтрольная
    Дата17.11.2021
    Размер1.13 Mb.
    Формат файлаdoc
    Имя файлаПримеры выполнения контр.doc
    ТипДокументы
    #274308
    страница2 из 2
    1   2
    Часть 3

    «Обработка результатов многократных измерений»
    В таблице 1 приведены 100 независимых числовых значений результата измерения. Проверить гипотезу о нормальности распределения вероятности результатов измерения. Записать результат в принятой форме, исходя из уровня доверительной вероятности Р=0,98. Представить два варианта доверительного интервала - для нормального и для неизвестного закона распределения вероятности среднего арифметического значения измеряемой величины.

    Таблица 1.


    30,36
    29,99
    30,41
    30,08
    30,17
    30,30
    30,10
    30,33
    30,43
    30,19

    30,38
    29,90
    29,94
    30,32
    30,35
    30,48
    30,32
    30,19
    30,24
    29,84

    30,08
    30,02
    30,09
    30,02
    30,37
    30,14
    30,25
    30,10
    30,15
    30,13

    29,93
    30,00
    30,32
    30,24
    30,14
    30,31
    30,28
    30,22
    30,12
    30,19

    30,10
    30,24
    30,16
    30,17
    30,23
    30,00
    30,13
    30,02
    30,34
    30,16

    29,88
    30,30
    30,17
    30,15
    30,17
    30,13
    30,29
    30,26
    30,35
    30,18

    30,48
    30,02
    30,20
    30,11
    30,37
    29,97
    29,97
    30,00
    30,09
    30,35

    30,18
    30,29
    29,88
    30,15
    30,29
    30,12
    30,19
    30,31
    30,13
    30,25

    30,19
    30,13
    29,88
    30,37
    30,24
    30,10
    30,07
    30,00
    30,14
    30,22

    30,09
    30,22
    30,22
    30,07
    30,14
    29,83
    30,01
    29,96
    30,22
    30,15


    1. Определим среднее арифметическое и стандартное отклонение для данных таблицы 1: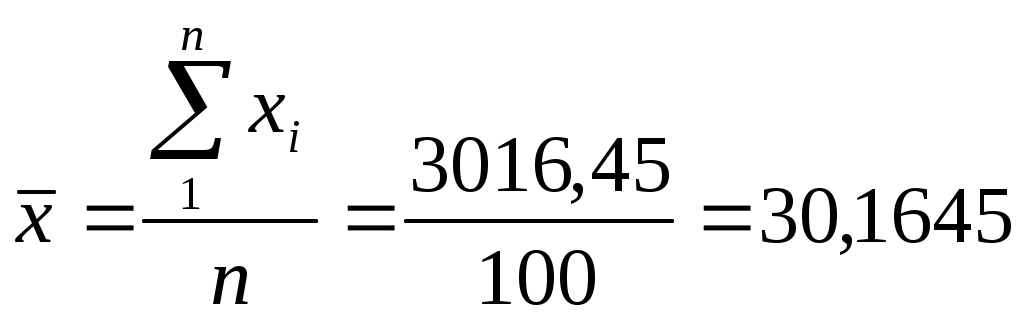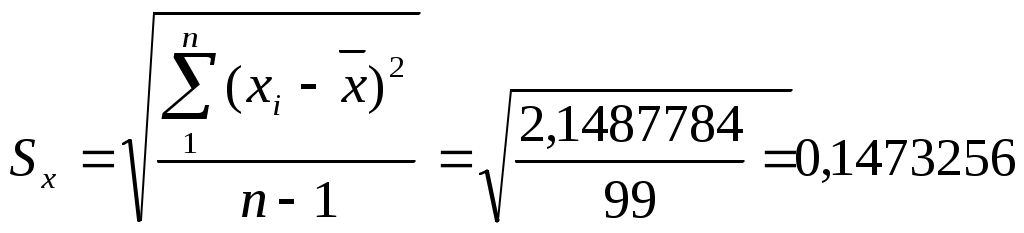





    2. С помощью правила «трех сигм» проверяем наличие или отсутствие промахов.





    Таким образом, ни один из результатов не выходит за границы интервала , следовательно, с вероятностью 0,9973 гипотеза об отсутствии грубых погрешностей принимается.

    3. Построение гистограммы и выдвижение гипотезы о виде закона распределения вероятности.

    Для того чтобы построить гистограмму, необходимо результаты отдельных измерений расположить в так называемый вариационный ряд по возрастанию их численных значений.

    Участок оси абсцисс, на котором располагается вариационный ряд значений физической величины, разбивается на k одинаковых интервалов . При выборе числа интервалов следует придерживаться следующих рекомендаций:


    Число измерений «n»
    Число интервалов «k»

    40-100
    7-9

    100-500
    8-12

    500-1000
    10-16

    1000-10000
    12-22


    Тогда:



    Начало первого интервала выбирается таким образом, чтобы это значение оказалось меньше, чем минимальный результат вариационного ряда. Последний интервал должен покрывать максимальное значение ряда. Выберем начало первого интервала в точке 29,87, тогда конец последнего (9-го) интервала окажется в точке 30,5.

    Затем для каждого интервала подсчитывается количество результатов mi, попавших в данный интервал и определяется



    Если в интервал попадает меньше пяти наблюдений, то такие интервалы объединяют с соседними, соответственно изменяется и параметр .

    начало окончание кол-во совпадений mi

    - первый интервал составляет 29,87 до 29,94 6

    - второй интервал составляет 29,94 до 30,01 9

    - третий интервал составляет 30,01 до 30,08 8

    - четвертый интервал составляет 30,08 до 30,15 22

    - пятый интервал составляет 30,15 до 30,22 17

    - шестой интервал составляет 30,22 до 30,29 12

    - седьмой интервал составляет 30,29 до 30,36 13

    - восьмой интервал составляет 30,36 до 30,43 6

    примем m =8

    - девятый интервал составляет 30,43 до 30,50 2

    Так, в нашем примере объединяются два последних интервала, их ширина становится равной 0,14. Общее число интервалов становится равным 8.

    Результаты производимых вычислений заносятся в первую половину таблицы 2, а затем строится сама гистограмма (рис.1).

    Определяем для каждого из интервалов.

    ; ; ; ; ; ; ;

    Построим гистограмму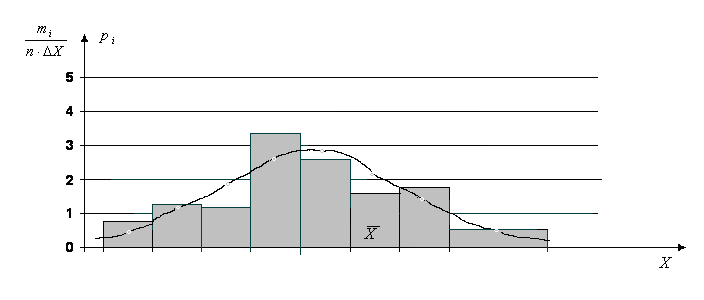

    Рис.1
    Из вида гистограммы на рис. 1 можно сделать предположение о том, что вероятность результата измерения подчиняется нормальному закону. Проверим правдивость этой гипотезы.

    4. Проверка нормальности закона распределения по критерию Пирсона.

    Для расчета критерия Пирсона необходимо знать эмпирические частоты и теоретические вероятности для каждого интервала . Для расчета вероятностей используется функция Лапласа:



    Значения X1 и X2 соответствуют началу и концу интервала. Для каждого из этих значений рассчитываем относительный доверительный интервал t, а затем из таблиц функции Лапласа находим соответствующие значения этой функции и .

    Рассчитаем значение относительного доверительного интервала t для каждого из интервалов.

    ;

    ; ;Из таблицы найдем

    ; ; ; ;

    ; ; ; ;

    ; ; ; ;

    ; ; ; ;

    ; ; ; ;

    ; ; ; ;

    ; ; ;

    ;

    Определим значение P для каждого интервала:

    ; ; ; ; ; ; ;



    Рассчитаем значение – критерия для каждого интервала и суммарное значение :

    ; ; ; ; ; ; ;





    Определим табличное (критическое) значение , задавшись доверительной вероятностью 0,98 и вычислив по формуле число степеней свободы:

    ; ; ;

    Таким образом, с вероятностью 0,98 гипотеза о нормальности распределения вероятности результата измерения принимается.

    5. В тех же координатах, что и гистограмма, следует построить теоретическую кривую плотности вероятности. Для этого рассчитываем значения плотности вероятности для середины каждого интервала и отложим как ординаты из середин соответствующих интервалов; полученные точки соединим плавной кривой, симметричной относительно математического ожидания (среднего арифметического значения) (рис 1).

    ; ; ; ; ; ; ;
    Результаты вычислений

    Таблица 2


    i
    Интервалы
    mi


















    1
    29,87
    29,94
    6
    0,857
    -1,999
    -1,524
    -0,4767
    -0,4357
    0,041
    0,88

    2
    29,94
    30,01
    9
    1,286
    -1,524
    -1,049
    -0,4357
    -0,3531
    0,0826
    0,066

    3
    30,01
    30,08
    8
    1,143
    -1,049
    -0,574
    -0,3531
    -0,2157
    0,1374
    2,398

    4
    30,08
    30,15
    22
    3,143
    -0,574
    -0,098
    -0,2157
    -0,0398
    0,1759
    1,106

    5
    30,15
    30,22
    17
    2,429
    -0,098
    -0,377
    -0,0398
    0,1480
    0,1878
    0,169

    6
    30,22
    30,29
    12
    1,714
    -0,377
    0,852
    0,1480
    0,3023
    0,1543
    0,762

    7
    30,29
    30,36
    13
    1,857
    0,852
    1,327
    0,3023
    0,4082
    0,1059
    0,548

    8
    30,36
    30,43
    6

    0,571

    1,327

    2,277

    0,4082

    0,4887

    0,0805

    0,0003

    9
    30,43
    30,50
    2


    6. Представление результата в виде доверительного интервала.

    Определим стандартное отклонение среднего арифметического по формуле:



    Закон распределения вероятности для среднего арифметического считаем нормальным, тогда доверительный интервал определяется по выражению при доверительной вероятности 0,98. Этому значению соответствует аргумент функции Лапласа t = 2,32.

    ;

    ;

    Если закон распределения вероятности для среднего арифметического считаем неизвестным, то относительный доверительный интервал рассчитываем в соответствии с неравенством Чебышева:

    ; ;

    ;

    ;

    Как видно из сравнения результатов, неизвестность закона распределения вероятности приводит к расширению доверительного интервала, то есть к увеличению дефицита измерительной информации.

    Список используемой литературы.


    1. Борискин, Соловьев, Белов, Якушенков. Методическое пособие «Расчет параметров посадки и калибров для проверки отверстия и вала».-т; 1994.

    2. Маликов А.Б., Анихинова М.А. Методическое пособие «Расчет сборочных размерных цепей методом полной взаимозаменяемости».-т; 1994.

    3. Борискин, Соловьев, Белов. Методическое пособие «Обработка результатов многократных измерений».

    4. Конспект лекций по курсу «Метрология, стандартизация, сертификация».

    5. ГОСТ 25347-82.

    6. ГОСТ 24853-81.

    7. ГОСТ 14807-69 – ГОСТ 14827-69.

    8. ГОСТ Р 50285-92 – ГОСТ Р 50288-92, ГОСТ 18369-73.

    9. ГОСТ 14748-69 – ГОСТ 14752-69.



    1   2

    написать администратору сайта