Статья на 25.08.2017-Кишинёв. Принцип профессиональной направленности
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
В ходе анализа различных теоретических подходов к определению профессионально-направленного обучения было выяснено, что большинство авторов видят принцип профессиональной направленности в качестве системообразующего принципа в профессиональном обучении студентов как высших, так и средних профессиональных учебных заведений. Несмотря на различные подходы к трактовке этого понятия, можно заключить, что авторы видят реализацию принципа за счет специального отбора содержания, выбора методов, форм и средств обучения, другими словами разработки педагогической технологии обучения математике в заданной образовательной системе. Если говорить о профессионально-направленном обучении математике, то большинство авторов видят специфику содержания в решении профессионально-ориентированных задач и реализацию таким образом, межпредметных связей математики со спецдисциплинами. Основная цель, на достижение которой направлено обучение математике в системе СПО технического профиля, – усвоение знаний и умений, необходимых для дальнейшего успешного изучения спецдисциплин, профессиональных модулей и профессиональной деятельности. Основными механизмами достижения выше обозначенной цели являются поддержание высокого уровня мотивации студентов, формирование устойчивого интереса к изучению спецдисциплин и будущей профессиональной деятельности. С учетом вышесказанного достаточно полным определением профессиональной направленности является определение, данное М. И. Махмутовым. Он пишет, что принцип профессиональной направленности обучения заключается «в своеобразном использовании педагогических средств, при котором обеспечивается усвоение учащимися предусмотренных программами знаний, умений, навыков и в то же время успешно формируются интерес к данной профессии, ценностное отношение к ней, профессиональные качества личности будущего рабочего» [32]. Прокомментируем определение, данное М. И. Махмутовым принципу профессиональной направленности с учетом специфики обучения математике в системе СПО технического профиля. Во-первых, в содержании понятия заложена одна из главных целей обучения математике – усвоение учащимися предусмотренных программами знаний, умений, навыков, осуществляемое не только на заданиях чисто математического содержания, но и посредством выполнения специфичных профессионально-ориентированных заданий. Во-вторых, в определении приведена еще одна задача, решаемая средствами профессионально-ориентированного обучения, – повышение учебной мотивации через формирование интереса к будущей профессии и профессионально важных качеств личности. Эта задача является метапредметной, мы видим ее решение в расширении у обучающихся представлений о прикладной и профессиональной значимости математики через непрерывную демонстрацию возможностей применения математических знаний и умений при изучении спецдисциплин. Эти подходы положены в основу разработанной нами дидактической модели и профессионально-ориентированной педагогической технологии обучения математике в системе СПО. Для профессионально-ориентированного обучения принцип профессиональной направленности является доминирующим, все остальные принципы обучения подчинены ему. Специфика профессионально-ориентированного обучения математике в системе СПО технического профиля заключается в следующем. Цели обучения в школе и в вузе монолитны: получение общего математического или профессионально-математического образования соответственно. Цель обучения в техникуме композитная: завершить школьное математическое образование и получить профессионально-математическое. Анализ учебных планов показал, что по всем специальностям технического профиля параллельно с математикой изучается ряд спецдисциплин и профессиональных модулей, в которых востребованы знания и умения, приобретаемые в результате изучения математических дисциплин. Так на специальности «Компьютерные системы и комплексы» в дисциплине «Электротехника» востребованы знания по темам «Теория матриц», «Решение систем линейных уравнений», «Интегральное исчисление» и «Комплексные числа». На специальности «Монтаж и техническая эксплуатация промышленного оборудования» при изучении дисциплины «Техническая механика» нужны знания по темам «Решение систем линейных уравнений», «Дифференциальное и интегральное исчисление». По этой причине установление межпредметных связей носит в колледжах особый смысл: удовлетворение потребностей спецдисциплин в применении математических методов решения задач, выстраивание последовательности изучения разделов согласно хронологии изучения соответствующих методов решения задач на спецдисциплинах. Рассмотрим применение раздела «Теория матриц» при изучении спецдисциплин специальности «Компьютерные системы и комплексы».
Необходимо составить систему уравнений и рассчитать токи в ветвях по законам Кирхгофа для заданной схемы с исходными данными (рис. 1) 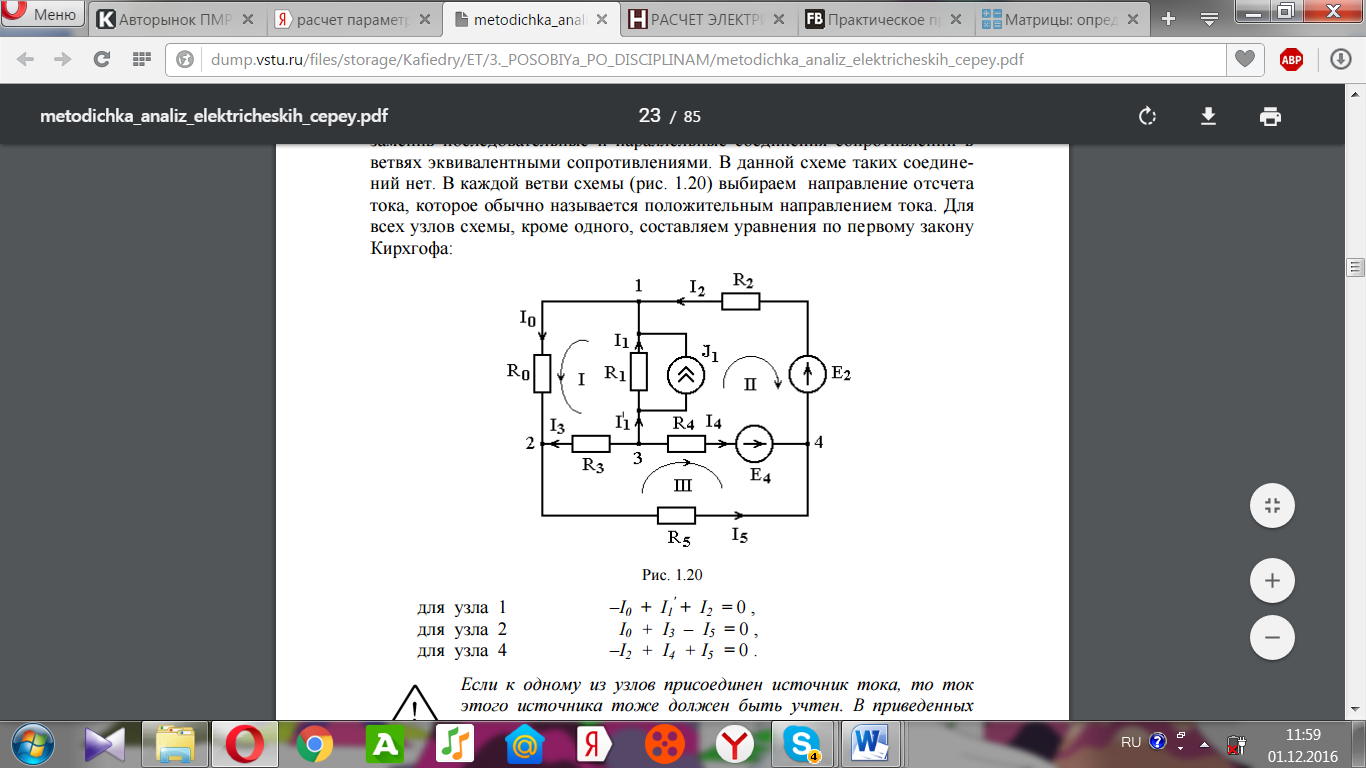 Рисунок 1. Электрическая цепь Решение. При расчете по возможности необходимо упростить схему, заменив последовательные и параллельные соединения сопротивлений в ветвях эквивалентными сопротивлениями. В данной схеме таких соединений нет. В каждой ветви схемы (рис. 1) выбираем направление отсчета тока, которое обычно называется положительным направлением тока. Для всех узлов схемы, кроме одного, составляем уравнения по первому закону Кирхгофа: для узла 1 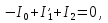 для узла 2 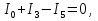 для узла 4 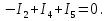 Если к одному из узлов присоединен источник тока, то ток этого источника тоже должен быть учтен. В приведенных выше уравнениях ток источника тока учитывается в уравнении, составленном для узла I, где 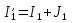 . .Подставив это выражение в уравнение, составленное для узла 1, получим 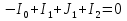 или  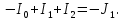 Поэтому в цепях с источниками тока первый закон Кирхгофа целесообразно записывать в следующем виде: 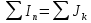 . .То есть алгебраическая сумма токов в ветвях равна алгебраической сумме токов, обусловленных источниками тока. При этом выбор знаков перед Jк аналогичен выбору знаков для обычных токов ветвей. Для составления уравнений по второму закону Кирхгофа необходимо выбрать независимые контуры, число которых равно числу недостающих уравнений. Выбираем независимые контуры, и указываем стрелками положительные направления обхода в каждом из них (рис. 1). Затем для каждого контура составляем уравнения по второму закону Кирхгофа: для контура I 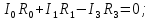 для контура II 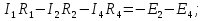 для контура III 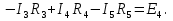 Уравнения Кирхгофа представим в матричной форме:  Подставим значения сопротивлений и рассчитаем матрицу-столбец токов.  В результате расчетов получены следующие значения токов: 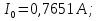 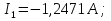 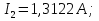 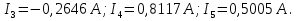 2.  |
