2 Практическая работа. Принципы работы классических алгоритмов шифрования
 Скачать 246.73 Kb. Скачать 246.73 Kb.
|
1.3 Шифрование методом перестановкиПри шифровании перестановкой символы шифруемого текста переставляются по определенным правилам внутри шифруемого блока этого текста. Простая перестановка Выбирается размер блока шифрования в n столбцов и m строк и ключевая последовательность, которая формируется из натурального ряда чисел 1,2,...,n случайной перестановкой. Шифрование проводится в следующем порядке: Шифруемый текст записывается последовательными строками под числами ключевой последовательности, образуя блок шифрования размером n*m. Зашифрованный текст выписывается колонками в порядке возрастания номеров колонок, задаваемых ключевой последовательностью. Заполняется новый блок и т.д. Например, зашифруем текст ГРУЗИТЕ_АПЕЛЬСИНЫ_БОЧКАХ блоком размером 8*3 и ключом 5-8-1-3-7-4-6-2. Таблица простой перестановки будет иметь вид:
Зашифрованное сообщение: УЕБ_НХЗЛОЕСЛГАЫЕИАИЬЧРП_ Расшифрование выполняется в следующем порядке: Из зашифрованного текста выделяется блок символов размером n*m. Этот блок разбивается на n групп по m символов. Символы записываются в те столбцы таблицы перестановки, номера которых совпадают с номерами групп в блоке. Расшифрованный текст читается по строкам таблицы перестановки. Выделяется новый блок символов и т.д. Перестановка, усложненная по таблице При усложнении перестановки по таблицам для повышения стойкости шифра в таблицу перестановки вводятся неиспользуемые клетки таблицы. Количество и расположение неиспользуемых элементов является дополнительным ключом шифрования. При шифровании текста в неиспользуемые элементы не заносятся символы текста и в зашифрованный текст из них не записываются никакие символы - они просто пропускаются. При расшифровке символы зашифрованного текста также не заносятся в неиспользуемые элементы. Для дальнейшего увеличения криптостойкости шифра можно в процессе шифрования менять ключи, размеры таблицы перестановки, количество и расположение неиспользуемых элементов по некоторому алгоритму, причем этот алгоритм становится дополнительным ключом шифра. Перестановка, усложненная по маршрутам Высокую стойкость шифрования можно обеспечить усложнением перестановок по маршрутам типа гамильтоновских. При этом для записи символов шифруемого текста используются вершины некоторого гиперкуба, а знаки зашифрованного текста считываются по маршрутам Гамильтона, причем используются несколько различных маршрутов. Для примера рассмотрим шифрование по маршрутам Гамильтона при n=3. Струкрура трехмерного гиперкуба представлена на рисунке 6. 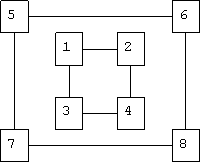 Рисунок 6. Трехмерный гиперкуб Номера вершин куба определяют последовательность его заполнения символами шифруемого текста при формировании блока. В общем случае n-мерный гиперкуб имеет n2 вершин. 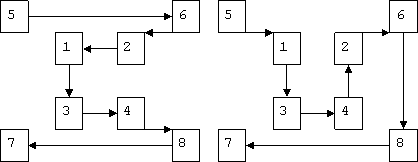 Рисунок 7. Маршруты Гамильтона Последовательность перестановок символов в шифруемом блоке для первой схемы 5-6-2-1-3-4-8-7, а для второй 5-1-3-4-2-6-8-7. Аналогично можно получить последовательность перестановок для других маршрутов: 5-7-3-1-2-6-8-4, 5-6-8-7-3-1-2-4, 5-1-2-4-3-7-8-6 и т.д. Размерность гиперкуба, количество вид выбираемых маршрутов Гамильтона составляют секретный ключ метода. Стойкость простой перестановки однозначно определяется размерами используемой матрицы перестановки. Например, при использовании матрицы 16*16 число возможных перестановок достигает 1.4E26. Такое число вариантов невозможно перебрать даже с использованием ЭВМ. Стойкость усложненных перестановок еще выше. Однако следует иметь в виду, что при шифровании перестановкой полностью сохраняются вероятностные характеристики исходного текста, что облегчает криптоанализ. Метод простой перестановкиПри шифровании методом простой перестановки производят деление открытого текста на блоки одинаковой длины, равной длине ключа. Ключ длины n представляет собой последовательность неповторяющихся чисел от 1 до n. Символы открытого текста внутри каждого из блоков переставляют в соответствие с символами ключа внутри блока справа налево.Элемент ключа Ki в заданной позиции блока говорит о том, что на данное место будет помещен символ открытого текста с номером Ki из соответствующего блока. Пример 5.3. Зашифруем открытый текст «ПРИЕЗЖАЮДНЕМ» методом перестановки с ключом К=3142.
Для дешифрования шифротекста необходимо символы шифротекста перемещать в позицию, указанную соответствующим им символом ключа Ki слева направо. Алгоритм ГамильтонаВесьма высокую стойкость шифрования можно обеспечить усложнением перестановок по маршрутам типа гамильтоновских. При этом, для записи символов шифруемого текста используются вершины некоторого гиперкуба, а знаки зашифрованного текста считываются по маршрутам Гамильтона, причем используется восемь различных маршрутов. Размер ключа перестановки в данном случае равен восьми по числу вершин куба. Для примера, два из маршрутов Гамильтона представлено на рис. 4.2. Первому маршруту соответствует перестановка 4-0-2-3-1-5-7-6, второму 4-6-2-0-1-5-7-3 (нумерация символов в блоке осуществляется с нуля). 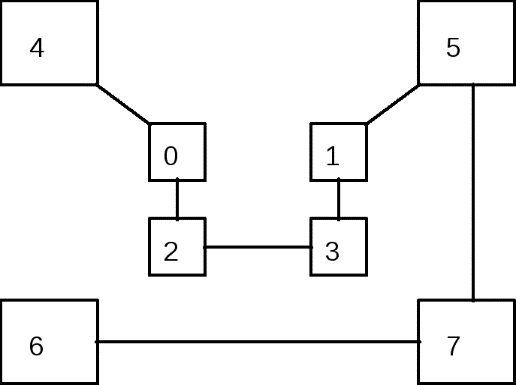 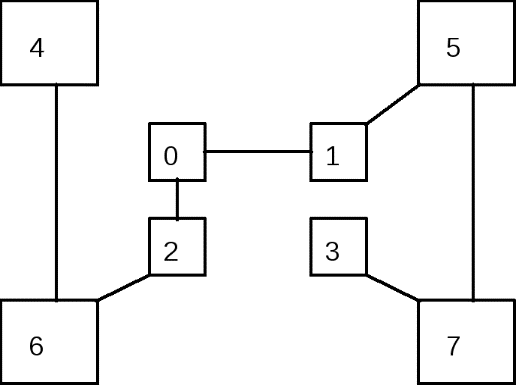 Рис. 5.1. Пример маршрутов Гамильтона Пример 5.4. Зашифруем открытый текст «ВОСЕМЬ МАРШРУТОВ» с помощью перестановок Гамильтона при использовании в качестве ключа двух перестановок, представленных на рис. 5.1.
Шифрование по методу Вернама Пример Берём латинского алфавита и обозначаем в двоичному кодированию. 25 латинский букв и 7 произвольной символы. Общие число составляет 32 символов Каждую буквы и символы преобразуем в порядковую и двоичную кодировку Для шифрование текста организуем сложение по mod2 (ХОR) . Здесь слагаемое исходный текст и ключ A=0=00000 N=13=01101 #=26=11010 B=1=00001 O=14=01110 !=27=11011 C=2=00010 P=15=01111 _=28=11100 D=3=00011 Q=16=10000 @=29=11101 E=4=00100 R=17=10001 ?=30=11110 F=5=00101 S=18=10010 *=31=11111 G=6=00110 T=19=10011 H=7=00111 U=20=10100 I=8=01000 V=21=10101 J=9=01001 W=22=10110 K=10=01010 X=23=10111 L=11=01011 Y=24=11000 M=12=01100 Z=25=11001 T1=T0+K Исходный текст T0 = USMANBAYEV_DONIYORBEK_SHUHRATOVICH Ключ K = TALABA Сложение по mod2 представляют:
Процесс преобразование и шифрование : U 10100 S 10010 M 01100 A 00000 + + + + T 10011 A 00000 L 01011 A 00000 = = = = H 00111 S 10010 H 00111 A 00000 В результате : T1=T0+K T1 = HSHAMBTYPV@D@NDYPRSEB_THHH#ASOGIJH Срок сдачи дидлайна для 2-практическая работу до 22 октябрь 2019 г. Выпольненный работы оценивается только после проверки преподавателя ! |
