ОСА_ПР№2_Насонова_С_А_2023. Принятие решений в условия риска и неопределенности

• Название: Принятие решений в условия риска и неопределенности
• Дата: 23.05.2023
• Размер: 89.17 Kb.
• Имя файла: ОСА_ПР№2_Насонова_С_А_2023.docx
• Тип: Документы; #1154723

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Ижевский государственный технический университет имени М. Т. Калашникова»

Кафедра АСОИУ

ОТЧЁТ

по практической работе № 2

по дисциплине «Основы системного анализа»

на тему «Принятие решений в условия риска и неопределенности»


Выполнил

студент гр. Б20-782-1зу С. А. Насонова
Проверил

канд. физ.-мат. наук, доцент кафедры АСОИУ Е. В. Касаткина

Ижевск 2023

Постановка задачи

Возможно строительство 8 электростанций. Эффективность каждого из типов зависит от различных факторов. Предполагается, что выделено 6 различных состояний, каждое из которых означает определенное сочетание влияющих на эффективность объектов факторов. Экономическая эффективность отдельных типов электростанций задана матрицей А (см. исходные данные). Строки соответствуют различным альтернативам, столбцы – состояниям среды.

Задание

1. 
   Принять решение о строительстве электростанции с использованием классических критериев:
   

1. 
   критерий Вальда;
   
2. 
   критерий азартного игрока;
   
3. 
   критерий Гурвица (установить диапазоны принятия различных альтернатив при λϵ[0; 1]);
   
4. 
   критерий Лапласа;
   

2. 
   Принять решение о строительстве электростанции с использованием критериев с сожалениями:
   

1. 
   критерий Сэвиджа;
   
2. 
   критерий Лапласа с сожалениями;
   
3. 
   критерий субъективно-средних сожалений;
   

3. 
   Принять решение о строительстве электростанции при учете заданных вероятностей с использованием критериев:
   

1. 
   критерий максимальной вероятности;
   
2. 
   критерий Байеса;
   
3. 
   критерий Ходжа-Лемана (установить диапазоны принятия различных альтернатив при μϵ[0; 1]);
   
4. 
   критерий минимума дисперсии оценочного функционала.
   

4. 
   Провести анализ чувствительности принятого на основе критерия Байеса решения (рассмотреть не менее 10 наборов вероятностей).
   
5. 
   Найти Парето оптимальные решения и принять решение с использованием правила одновременного учета среднего ожидаемого дохода и среднего ожидаемого риска, понимаемого как стандартное отклонение (4*M(Fi) – 3*σ(Fi)).
   
6. 
   Провести исследование решения, полученного по критерию Байеса в случае обращения в консалтинг. Базируясь на байесовском подходе, а также учитывая статистическую информацию о деятельности консалтинговой фирмы, сделать вывод об оценке стоимости консалтинговых услуг, при которой обращение в эту фирму окажется выгодным для ЛПР. Нарисовать полное дерево решений для обоснования полученных выводов при обращении в консалтинг.
   

Вариант 13

A1	53	91	129	130	108	50
A2	37	37	54	60	141	86
A3	105	138	28	71	43	-3
A4	67	138	47	33	15	130
A5	64	-5	16	146	123	83
A6	29	14	-6	-2	76	75
A7	-8	46	41	46	38	107
A8	101	81	23	150	84	15
pi	0.1	0.09	0.22	0.22	0.3	0.007

Статистические данные о надежности прогнозов имеют следующий вид (Условные вероятности правильности прогноза):

Реальные состояния	Прогноз
S1	0,6	0,3	0,05	0,02	0,02	0,01
S2	0,15	0,6	0,15	0,05	0,025	0,025
S3	0,05	0,2	0,6	0,1	0,025	0,025
S4	0,05	0,05	0,15	0,6	0,1	0,05
S5	0	0,025	0,025	0,2	0,6	0,15
S6	0	0	0,05	0,1	0,25	0,6

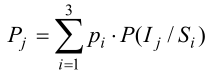Полные вероятности: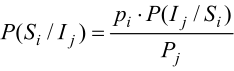



Апостериорные вероятности:
Для определения наиболее предпочтительного типа электростанции можно умножить каждый элемент матрицы А на соответствующий элемент вектора pj, а затем сложить результаты для каждого типа электростанции.

Например, для расчета эффективности первого типа электростанции можно выполнить следующую операцию:

A1: (53*0.1) + (91*0.09) + (129*0.22) + (130*0.22) + (108*0.3) + (50*0.07) = 106.37

Аналогичные операции можно выполнить для всех типов электростанций и выбрать тот, у которого результат будет наибольшим.

Таким образом, для принятия решения о выборе типа электростанции нужно выполнить математическое моделирование, учитывающее данные матрицы А и вектора pj.

A2: (37*0.1) + (37*0.09) + (54*0.22) + (60*0.22) + (141*0.3) + (86*0.07) = 80.43

A3: (105*0.1) + (138*0.09) + (28*0.22) + (71*0.22) + (43*0.3) + (-3*0.07) = 57.39

A4: (67*0.1) + (138*0.09) + (47*0.22) + (33*0.22) + (15*0.3) + (130*0.07) = 50.32

A5: (64*0.1) + (-5*0.09) + (16*0.22) + (146*0.22) + (123*0.3) + (83*0.07) = 84.3

A6: (29*0.1) + (14*0.09) + (-6*0.22) + (-2*0.22) + (76*0.3) + (75*0.07) = 30.45

A7: (-8*0.1) + (46*0.09) + (41*0.22) + (46*0.22) + (38*0.3) + (107*0.07) = 41.37

A8: (101*0.1) + (81*0.09) + (23*0.22) + (150*0.22) + (84*0.3) + (15*0.07) = 81.7

Наибольшим значением эффективности будет A1 = 106.37

1. 
   Принять решение о строительстве электростанции с использованием классических критериев:
   

1. 
   критерий Вальда
   

Строим матрицу:

Ai	П1	П2	П3	П4	П5	П6	min(A)
A1	53	91	129	130	108	50	50
A2	37	37	54	60	141	86	37
A3	105	138	28	71	43	-3	-3
A4	67	138	47	33	15	130	15
A5	64	-5	16	146	123	83	-5
A6	29	14	-6	-2	76	75	-6
A7	-8	46	41	46	38	107	-8
A8	101	81	23	150	84	15	15

Критерий Вальда для выбора типа электростанции определяется как наименьший элемент в каждой матрице А по строкам. Таким образом, для каждого состояния выбирается тип станции, который имеет наибольший минимальный элемент в соответствующей строке матрицы А:

Выбираем из(50; 37; -3; 15; -5; -6; -8; 15)

min=-8

Вывод: тип электростанции с наименьшим минимальным значением – A7, соответствует наибольшей осторожности и выбирается на основе критерия Вальда.

2. 
   критерий азартного игрока
   

Для критерия азартного игрока, выбирается альтернатива с максимальным значением максимума из всех возможных значений для каждой альтернативы и каждого состояния среды.

Вариант 13

Ai	П1	П2	П3	П4	П5	П6	max(A)
A1	53	91	129	130	108	50	130
A2	37	37	54	60	141	86	141
A3	105	138	28	71	43	-3	138
A4	67	138	47	33	15	130	138
A5	64	-5	16	146	123	83	146
A6	29	14	-6	-2	76	75	76
A7	-8	46	41	46	38	107	107
A8	101	81	23	150	84	15	150

Принятие решения:

Теперь выберем альтернативу с максимальным значением максимума из всех возможных значений. Исходя из расчетов, альтернатива с максимальным значением максимума имеет значение 150 и соответствует альтернативе A8.

Вывод: на основе критерия азартного игрока, рекомендуется выбрать альтернативу A8 - строительство электростанции.

3. 
   Критерий Гурвица
   

Для критерия Гурвица с параметром λ, необходимо найти максимум из взвешенных значений максимумов и минимумов для каждой альтернативы и каждого состояния среды. В данном случае, так как у нас задан диапазон значений параметра λ ∈ [0; 1], мы можем выбрать различные значения λ в этом диапазоне и оценить результаты.

Произведём расчет для λ = 0.5

A1 = λ * max(53, 91, 129,130, 108, 50) + (1 - λ) * min(53, 91, 129,130, 108, 50) = 0.5 * 130 + 0.5 * 50 = 90

A2 = λ * max(37, 37, 54, 60, 141, 86) + (1 - λ) * min(37, 37, 54, 60, 141, 86) = 0.5 * 141+ 0.5 * 37= 89

A3 = λ * max(105, 138, 28, 71, 43, -3) + (1 - λ) * min(105, 138, 28, 71, 43, -3) = 0.5 * 138 + 0.5 * -3 = 67.5

A4 = λ * max(67, 138, 47, 33, 15, 130) + (1 - λ) * min(67, 138, 47, 33, 15, 130) = 0.5 * 138 + 0.5 * 15 = 76.5

A5 = λ * max(64, -5, 16, 146, 123, 83) + (1 - λ) * min(64, -5, 16, 146, 123, 83) = 0.5 * 146+ 0.5 * -5 = 70.5

A6 = λ * max(29, 14, -6, -2, 76, 75) + (1 - λ) * min(29, 14, -6, -2, 76, 75) = 0.5 * 76 + 0.5 * -6 = 35

A7 = λ * max(-8, 46, 41, 46, 38, 107) + (1 - λ) * min(-8, 46, 41, 46, 38, 107) = 0.5 * 107 + 0.5 * -8 = 49.5

A8 = λ * max(101, 81, 23, 150, 84, 15) + (1 - λ) * min(101, 81, 23, 150, 84, 15) = 0.5 * 150 + 0.5 * 15 = 82.5

Таким образом, для параметра λ = 0.5, значения критерия Гурвица для всех альтернатив будут следующими:

max=90

Вывод: выбираем стратегию A1.

Определение диапазона принятия альтернатив

Диапазон принятия альтернатив можно определить, выбрав значения параметра λ в диапазоне [0; 1] и сравнив значения критерия Гурвица для каждой альтернативы. В данном случае, более высокие значения критерия Гурвица соответствуют более предпочтительным альтернативам.

Например, если мы выберем λ = 0.7, то значения критерия Гурвица будут следующими:

A1 = 0.7 * 130 + 0.3 * 50 = 106

A2 = 0.7 * 141 + 0.3 * 37 = 109.8

A3 = 0.7 * 138 + 0.3 * -3 = 95.7

A4 = 0.7 * 138 + 0.3 * 15 = 101.1

A5 = 0.7 * 146 + 0.3 * -5 = 100.7

A6 = 0.7 * 76 + 0.3 * -6= 51.4

A7 = 0.7 * 107 + 0.3 * -8 = 72.5

A8 = 0.7 * 150 + 0.3 * 15 = 109.5

Вывод: при λ = 0.7, наиболее предпочтительной альтернативой будет А2, так как она имеет наивысшее значения критерия Гурвица.

4. 
   Критерий Лапласа
   

Найдем математическое ожидание (среднее значение) для каждой альтернативы путем вычисления суммы значений в каждом столбце и деления на количество состояний среды:

Математическое ожидание (среднее значение):

А1: (53 + 91 + 129 +130 +108 + 50) / 6 = 93.5

А2: (37 + 37 + 54 + 60 + 141 + 86) / 6 = 69.2

А3: (105 + 138 + 28 + 71 + 43 + (-3)) / 6 = 63.7

А4: (67 + 138 + 47 + 33 + 15 + 130) / 6 = 71.7

А5: (64 +( -5) + 16 + 146 + 123 + 83) / 6 = 71.2

А6: (29 + 14 +( -6 )+ (-2)+ 76 + 75) / 6 = 31

А7: ((-8) + 46 + 41 + 46 + 38 + 107) / 6 = 45

А8: (101 + 81 + 23 + 150 + 84 +15) / 6 = 75.7

max=93.5

Вывод: Оптимальное решение по критерию Лапласа – А1

2. 
   Принять решение о строительстве электростанции с использованием критериев с сожалениями:
   

1. 
   Критерий Сэвиджа
   

Находим матрицу рисков:

1. Рассчитываем 1-й столбец матрицы рисков.
r₁₁ = 105 - 53 = 52; r₂₁ = 105 - 37 = 68; r₃₁ = 105 - 105 = 0; r₄₁ = 105 - 67 = 38; r₅₁ = 105 - 64 = 41; r₆₁ = 105 - 29 = 76; r₇₁ = 105 - (-8) = 113; r₈₁ = 105 - 101 = 4;
2. Рассчитываем 2-й столбец матрицы рисков.
r₁₂ = 138 - 91 = 47; r₂₂ = 138 - 37 = 101; r₃₂ = 138 - 138 = 0; r₄₂ = 138 - 138 = 0; r₅₂ = 138 - (-5) = 143; r₆₂ = 138 - 14 = 124; r₇₂ = 138 - 46 = 92; r₈₂ = 138 - 81 = 57;
3. Рассчитываем 3-й столбец матрицы рисков.
r₁₃ = 129 - 129 = 0; r₂₃ = 129 - 54 = 75; r₃₃ = 129 - 28 = 101; r₄₃ = 129 - 47 = 82; r₅₃ = 129 - 16 = 113; r₆₃ = 129 - (-6) = 135; r₇₃ = 129 - 41 = 88; r₈₃ = 129 - 23 = 106;
4. Рассчитываем 4-й столбец матрицы рисков.
r₁₄ = 150 - 130 = 20; r₂₄ = 150 - 60 = 90; r₃₄ = 150 - 71 = 79; r₄₄ = 150 - 33 = 117; r₅₄ = 150 - 146 = 4; r₆₄ = 150 - (-2) = 152; r₇₄ = 150 - 46 = 104; r₈₄ = 150 - 150 = 0;
5. Рассчитываем 5-й столбец матрицы рисков.
r₁₅ = 141 - 108 = 33; r₂₅ = 141 - 141 = 0; r₃₅ = 141 - 43 = 98; r₄₅ = 141 - 15 = 126; r₅₅ = 141 - 123 = 18; r₆₅ = 141 - 76 = 65; r₇₅ = 141 - 38 = 103; r₈₅ = 141 - 84 = 57;
6. Рассчитываем 6-й столбец матрицы рисков.
r₁₆ = 130 - 50 = 80; r₂₆ = 130 - 86 = 44; r₃₆ = 130 - (-3) = 133; r₄₆ = 130 - 130 = 0; r₅₆ = 130 - 83 = 47; r₆₆ = 130 - 75 = 55; r₇₆ = 130 - 107 = 23; r₈₆ = 130 - 15 = 115;

Ai	П1	П2	П3	П4	П5	П6
A1	52	47	0	20	33	80
A2	68	101	75	90	0	44
A3	0	0	101	79	98	133
A4	38	0	82	117	126	0
A5	41	143	113	4	18	47
A6	76	124	135	152	65	55
A7	113	92	88	104	103	23
A8	4	57	106	0	57	115

Результаты вычислений оформим в виде таблицы.

Ai	П1	П2	П3	П4	П5	П6	max(aij)
A1	52	47	0	20	33	80	80
A2	68	101	75	90	0	44	101
A3	0	0	101	79	98	133	133
A4	38	0	82	117	126	0	126
A5	41	143	113	4	18	47	143
A6	76	124	135	152	65	55	152
A7	113	92	88	104	103	23	113
A8	4	57	106	0	57	115	115

Выбираем из (80; 101; 133; 126; 143; 152; 113; 115) минимальный элемент min=80.
Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A1.

б) Критерий Лапласа с сожалениями

Ожидаемый выигрыш каждой альтернативы вычисляется как сумма произведений вероятностей на выигрыши в каждом из возможных исходов. Для каждой альтернативы получим:

А1: 0.1 * 53 + 0.09 * 91 + 0.22 * 129+ 0.22 * 130+ 0.3 * 108 + 0.07 * 50= 106.37

А2: 0.1 *37 + 0.09 * 37 + 0.22 * 54 + 0.22 * 60 + 0.3 * 141 + 0.07 * 86= 80.43

А3: 0.1 * 105+ 0.09 * 138 + 0.22 * 28 + 0.22 * 71 + 0.3 * 43 + 0.07 * (-3) = 57.39

А4: 0.1 * 67 + 0.09 * 138 + 0.22 * 47 + 0.22 * 33 + 0.3 * 15 + 0.07 * 130 = 50.32

А5: 0.1 * 64 + 0.09 * (-5) + 0.22 * 16 + 0.22 * 146 + 0.3 * 123 + 0.07 * 83 = 84.3

А6: 0.1 * 29 + 0.09 * 14 + 0.22 *(-6) + 0.22 * (-2) + 0.3 * 76+ 0.07 * 75 = 30.45

А7: 0.1 * (-8) + 0.09 * 46 + 0.22 * 41 + 0.22 * 46 + 0.3 * 38 + 0.07 * 107 = 41.37

А8: 0.1 * 101 + 0.09 * 81 + 0.22 * 23 + 0.22 * 150+ 0.3 * 84 + 0.07 * 15 = 81.7

Вывод: наибольший ожидаемый выигрыш у А1 с ожидаемым выигрышем 106.37.

с) критерий субъективно-средних сожалений;

Для определения лучшей альтернативы по критерию субъективно-средних сожалений необходимо посчитать значения критерия для каждой альтернативы и выбрать ту, у которой наименьшее значение.

Для этого нужно посчитать произведение каждого элемента матрицы А на соответствующую вероятность из вектора pj и просуммировать результаты для каждой альтернативы. Таким образом, для каждой альтернативы j, значение критерия Kссс(j) будет равно:

Kссс(j) = Σ(i=1 to 6) Aij * pj

Применяя эту формулу к матрице А и вектору вероятностей pj, мы можем вычислить значения критерия для каждой альтернативы:

Kссс(А1) = (53*0.1) + (91* 0.09) + (129*0.22)+ (130*0.22) + (108*0.3) +(50*0.07)= 106.37

Kссс(А2) = (0.1 *37) + (37*0.09 ) + (54*0.22 ) + (60*0.22 ) + (141*0.3) + (86*0.07)= 80.43

Кссс(А3)= ( 105*0.1)+ (138*0.09) + (28*0.22) + (71*0.22) + (43*0.3) + ( (-3)* 0.07)= 57.39

Кссс(А4)= (67*0.1) + (138*0.09) + (47*0.22) + (33*0.22 ) + (15*0.3 ) + (130*0.07) = 50.32

Кссс(А5)= (64*0.1) + ( (-5) *0.09) + (16*0.22) + ( 146 *0.22 ) + (123*0.3)+ (83*0.07) = 84.3

Кссс(А6)= ( 29*0.1) + (14*0.09) + ((-6) *0.22) + ( (-2) *0.22 ) + (76*0.3)+ (75*0.07) = 30.45

Кссс(А7)= ((-8) *0.1) + (46*0.09) + (41*0.22) + ( 46*0.22) + (38* 0.3)+ (107* 0.07) = 41.37

Кссс(А8)= (101*0.1) + (81*0.09) + (23*0.22) + (150*0.22) + (84* 0.3) + (15*0.07) = 81.7

Вывод: лучшей альтернативой является А1 так как она имеет наибольшее значение Kссс.

3. Принять решение о строительстве электростанции при учете заданных вероятностей с использованием критериев:

1. 
   критерий Байеса
   

По критерию Байеса за оптимальные принимается та стратегия (чистая) Ai, при которой максимизируется средний выигрыш a или минимизируется средний риск r.

Считаем значения ∑(aijpj):

∑(a1,jpj) = 53*0.1+ 91* 0.09 + 129*0.22 + 130*0.22 + 108*0.3 +50*0.07= 106.37

∑(a2,jpj) = 0.1 *37 + 37*0.09 + 54*0.22 + 60*0.22 + 141*0.3 + 86*0.07 = 80.43

∑(a3,jpj) = 105*0.1 + 138*0.09 + 28*0.22 + 71*0.22 + 43*0.3 + (-3)* 0.07 = 57.39

∑(a4,jpj) = 67*0.1 + 138*0.09 + 47*0.22 + 33*0.22 + 15*0.3 + 130*0.07 = 50.32

∑(a5,jpj) = 64*0.1 + (-5) *0.09 + 16*0.22 + 146 *0.22 + 123*0.3 + 83*0.07 = 84.3

∑(a6,jpj) = 29*0.1 + 14*0.09 + (-6) *0.22 + (-2) *0.22 + 76*0.3 + 75*0.07 = 30.45

∑(a7,jpj) = (-8) *0.1 + 46*0.09 + 41*0.22 + 46*0.22 + 38* 0.3 + 107* 0.07 = 41.37

∑(a8,jpj) = 101*0.1 + 81*0.09 + 23*0.22 + 150*0.22 + 84* 0.3 + 15*0.07 = 81.7

Ai	П1	П2	П3	П4	П5	П6	∑(aijpj)
A1	5.3	8.19	28.38	28.6	32.4	3.5	106.37
A2	3.7	3.33	11,88	13.2	42.3	6.02	80.43
A3	10.5	12.42	6.16	15.62	12.9	-0.021	57.39
A4	6.7	12.42	10.34	7.26	4.5	9.1	50.32
A5	6.4	-0.45	3.52	32.12	36.9	5.81	84.3
A6	2.9	1.26	-1.32	-0.44	22.8	5.25	30.45
A7	-0.8	4.14	9.02	10.12	11.4	7.49	41.37
A8	10.1	7.29	5.06	33	25.2	1.05	81.7
pj	0.1	0.09	0.22	0.22	0.3	0.007

max=106.37

Вывод: выбираем стратегию A1.

2. 
   критерий Ходжа-Лемана (установить диапазоны принятия различных альтернатив при μϵ[0; 1]);
   

Для каждой строки рассчитываем значение критерия по формуле:

Wi = u∑aijpj + (1 - u)min(a)ij

Рассчитываем Wi.

W1 = 0.5*106.37 + (1-0.5)*50 = 78.185

W2 = 0.5*80.43 + (1-0.5)*37 = 58.715

W3 = 0.5*57.39 + (1-0.5)*(-3) = 27.195

W4 = 0.5*50.32 + (1-0.5)*15 = 32.66

W5 = 0.5*84.3 + (1-0.5)*(-5) = 39.65

W6 = 0.5*30.45 + (1-0.5)*(-6) = 12.225

W7 = 0.5*41.37 + (1-0.5)*(-8) = 16.685

W8 = 0.5*81.7 + (1-0.5)*15 = 48.35

Ai	П1	П2	П3	П4	П5	П6	∑(aijpj)	Wi
A1	5.3	8.19	28.38	28.6	32.4	3.5	106.37	78.185
A2	3.7	3.33	11,88	13.2	42.3	6.02	80.43	58.715
A3	10.5	12.42	6.16	15.62	12.9	-0.021	57.39	27.195
A4	6.7	12.42	10.34	7.26	4.5	9.1	50.32	32.66
A5	6.4	-0.45	3.52	32.12	36.9	5.81	84.3	39.65
A6	2.9	1.26	-1.32	-0.44	22.8	5.25	30.45	12.225
A7	-0.8	4.14	9.02	10.12	11.4	7.49	41.37	16.685
A8	10.1	7.29	5.06	33	25.2	1.05	81.7	48.35
pj	0.1	0.09	0.22	0.22	0.3	0.007

максимальный элемент max=78.185

Вывод: выбираем стратегию A1.