Принятие решений в условиях риска. Принятие решений в условиях риска
 Скачать 460.5 Kb. Скачать 460.5 Kb.
|
|
Лабораторная работа №3 Тема: Принятие решений в условиях риска Цель: Приобрести навыки поиска рациональных решений в условиях риска с использованием пакета MS Excel. Порядок выполнения работы: 1) Задание 1: определение наилучшей альтернативы в условиях риска Изучение примеров. Построение дерева принятия решений или таблицы платежей. Выбор критерия оценки качества решения (например, максимизация прибыли или минимизация затрат) Оценка полезности каждого из вариантов решений и выбор наилучшего решения. Анализ чувствительности полученного решения. 2) Задание 2: построение индивидуальной функции полезности Построение собственной функции полезности (в виде графика в MS Excel). Диапазон денежных сумм выбрать по своему усмотрению. Для сравнения, на том же графике построить прямую, отражающую нейтральное отношение к риску. Анализ полученной функции на предмет отношения к риску. 3) Составление отчёта по лабораторной работе, в котором представляется: формулировка индивидуального задания; дерево принятия решений (таблица платежей); снимки экрана монитора, содержащие результаты расчетов прибылей (затрат) возможных исходов, в соответствии с «деревом» и выводы о выбранном варианте решения; анализ чувствительности принятого решения. Выводы по результатам анализа; снимок экрана с построенной собственной функцией полезности и выводы, касающиеся собственного отношения к риску. Теория К задачам принятия решений в условиях риска, относятся задачи, исходные данные в которых можно описать с помощью вероятностных распределений. В подобных моделях термин риск имеет вполне определенный смысл: рассматривается несколько состояний природы, и мы можем сделать предположения о вероятностях наступления каждого возможного состояния природы. Если решение принимается в условиях риска, то стоимости альтернатив обычно описываются вероятностными распределениями. Т.е. прибыль (затраты), связанная с каждым альтернативным решением, является случайной величиной (вернут или вернут кредит: в одном случае мы получим прибыль, в другом — убытки). Поэтому в качестве критерия принятия решения используется ожидаемое значение стоимости — математическое ожидание (М). Все альтернативы сравниваются с точки зрения максимизации ожидаемой прибыли или минимизации ожидаемых затрат. Пример 1. Для финансирования проекта бизнесмену нужно занять сроком на один год 15000 долл. Банк может одолжить ему эти деньги под 15% годовых или вложить в дело со 100%-ным возвратом суммы, но под 9% годовых. Из прошлого опыта банкиру известно, что 4% таких клиентов ссуду не возвращают. Что делать? Давать ему заем или нет?  Построение дерева решений. Квадратные "узлы" обозначают места, где принимается решение (из квадрата выходят альтернативы); Круглые "узлы" — появление исходов (случайный выбор состояния природы). Численные значения доходов (исходы) просчитываются, начиная с конца "ветвей", постепенно приближаясь к исходному вопросу. Результат А1 = 15000 + 15% от 15000 = 17250 Результат A0 = 0 Результат B1 = 15000 + 9% от 15000 = 16350 Чистый доход, получаемый в случае выбора альтернативы А: M(давать заем) = (17250 * 0,96 + 0 * 0,04) - 15000 = 16500 - 15000 = 1560 долл. Выбор альтернативы B дает: M(не давать заем) = (16350 * 1,0 – 15000) = 1350 долл. Поскольку ожидаемый чистый доход больше для альтернативы А, то принимаем решение выдать заем. Анализ чувствительности. Решения, принимаемые при помощи «дерева», зависят от вероятностей исходов. Чувствительность решения определяется размером изменений вероятности. Выбирая решение, мы должны знать, насколько оно зависит от изменений вероятностей, и, следовательно, насколько можно полагаться на этот выбор. Проанализируем чувствительность в только что рассмотренном примере. Ожидаемые чистые доходы в «узлах» А и В довольно близки: 1560 и 1350 долл. Выбор решения зависит от значения вероятностей. Анализ чувствительности позволяет нам вычислить «разброс» вероятностей, которые меняют наш выбор. Обозначим вероятность «невозврата» займа через процесса через р. Тогда вариант А дает чистый доход 17250*(1-p) + 0*p – 15000 = 2250 – 17250*p Вариант В дает чистый доход 1350 долл. Уравнивание этих результатов дает: 2250 – 17250*p = 1350 => p = 900/17250 = 0,052 Поскольку результат p0,05 оказался близок к p0,04, это показывает, что выбор решения очень чувствителен к расчетам величины вероятности, и малейшая ошибка может привести к смене выбора. Что показывает важность анализа чувствительности в процессе принятия решений. Пример 2. Посредническая фирма еженедельно закупает и распространяет химические реактивы для фотолабораторий. Стоимость закупки ящика составляет 50 долл., прибыль от продажи ящика — 80 долл. Статистика исследования спроса приведена в таблице.
Если закупленный ящик остался непроданным, фирма несет убыток 50 долларов. Определить размер запаса, который целесообразно создать фирме. Изменится ли решение, если неудовлетворенный спрос клиента будет оценен в 45 долларов? Дерево решений запишется в виде 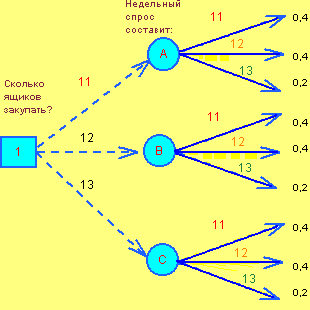 Итоговая таблица решения задачи в Excel (файл Фотобумага.XLS) имеет вид 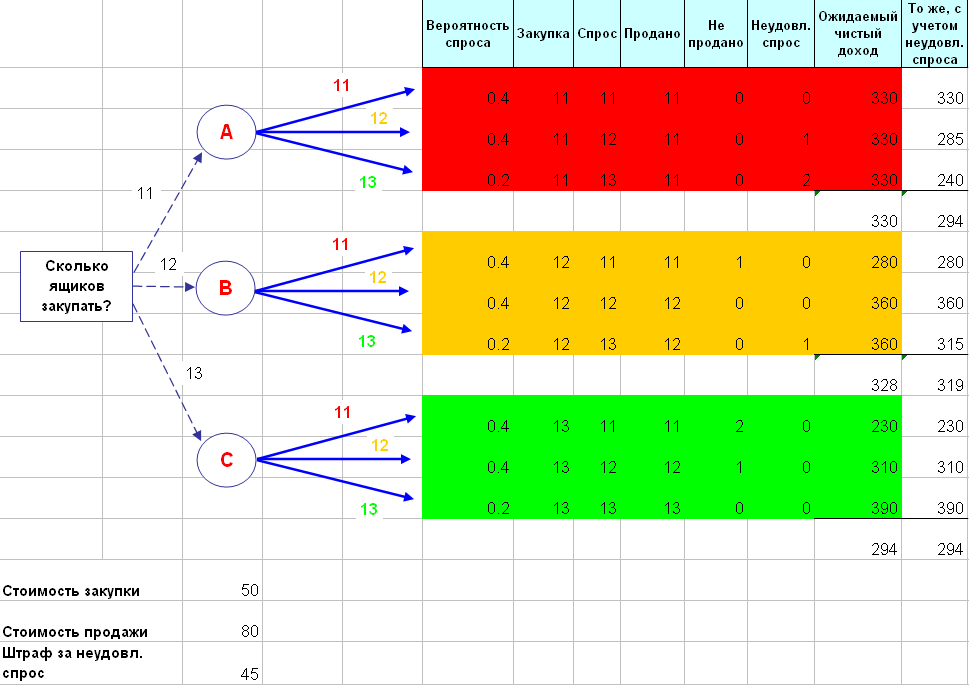 Ожидаемый чистый доход максимален при выборе альтернативы А (330 долл.). С учетом штрафов за неудовлетворенный спрос максимальный чистый доход дает альтернатива В (319 долл.). Пример 3. Банк решает вопрос, проверять ли конкурентоспособность клиента, перед тем, как выдавать заем. Аудиторская фирма берет с банка 80 ф. ст. за проверку. В результате этого перед банком встают две проблемы: первая проводить или нет проверку, вторая — выдавать после этого заем или нет. Решая первую проблему, банк проверяет правильность выдаваемых аудиторской фирмой сведений. Для этого выбираются 1000 человек, которые были проверены и которым впоследствии выдавались ссуды. Рекомендации аудиторской фирмы и возврат ссуды
Решение задачи состоит из следующих этапов. Этап. 1. Строим дерево решений (см. ниже). 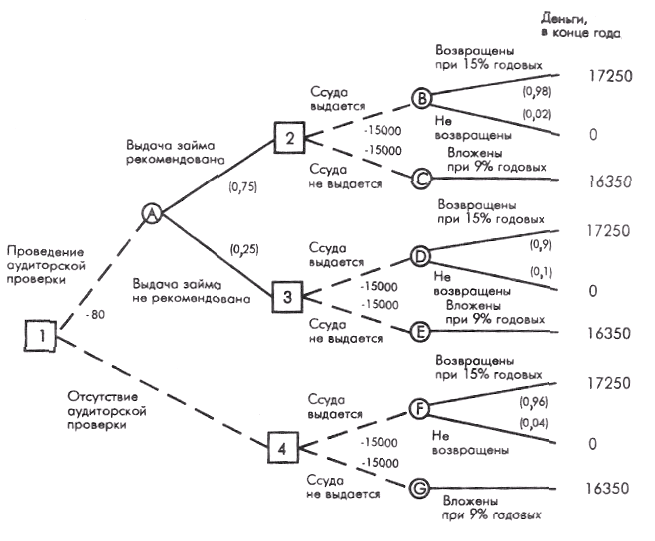 Этап 2. Используя данные таблицы, вычислим вероятности каждого исхода: Р (клиент ссуду вернет; фирма рекомендовала) = 735/750 = 0,98; Р (клиент ссуду не вернет; фирма рекомендовала) = 15/750 = 0,02; Р (клиент ссуду вернет; фирма не рекомендовала) = 225/ 250 = 0,9; Р (клиент ссуду не вернет; фирма не рекомендовала)= 25/250= 0,1. Этап 3. Слева направо проставим денежные исходы каждого из «узлов», используя результаты, вычисленные ранее. Любые встречающиеся расходы вычитаем из ожидаемых доходов. Таким образом подсчитываем все «дерево». После того, как пройдены квадраты «решений», выбирается «ветвь», ведущая к наибольшему из возможных при данном решении ожидаемому доходу. Сначала посмотрим на кружки исходов В и С, являющиеся следствием квадрата 2 (выдавать ли заем клиенту?) Доход, ожидаемый от исхода В: M (В) = 17250 долл. х 0,98 + 0 х 0,02 = 16905 долл.; чистый ожидаемый доход: NM (В) = 16905 - 15000 = 1905 долл. Доход, ожидаемый от исхода С: M (С) = 16350 долл. х 1,0 = 16350 долл.; чистый ожидаемый доход: NM (С) = 16350 - 15000 = 1350 ф. ст. Предположим, что мы сейчас в квадрате 2. Максимальный ожидаемый доход 1905 долл. достигается в кружке В, поэтому принимаем решение выдать заем. Приняв решение, корректируем «дерево», проставив чистый ожидаемый доход 1905 долл. над квадратом 2. «Ветвь» «не давать заем» зачеркивается. То же самое делаем с кружками исходов D и Е. Доход, ожидаемый от исхода D: M(D) = (17250 долл. х 0,9) + (0 х 0,1)= 15525 долл.; чистый ожидаемый доход: NM (D) = 15525 - 15000 = 525 долл. Аналогично для исхода Е: M (Е) = 16350 долл. х 1,0 = 16350 долл.; чистый ожидаемый доход: NМ (Е) = 16350 - 15000 = 1350 долл. Если бы мы были в квадрате 3, то максимальный ожидаемый доход был бы равен 1350 долл. и можно было бы принять решение не выдавать заем. Наконец приступаем к расчету кружков исходов F и G, которые являются результатами решения 4. М (F) = 17250 долл. х 0,96 + 0 х 0,04 = 16560 долл.; NМ (F) - 16560 - 15000 = 1560 долл.; М (G) = 16350 долл. х 1,0 = 16350 долл.; NМ (G) = 16350 - 15000 = 1350 долл. В квадрате 4 максимальный ожидаемый чистый доход составляет 1560 долл., и поэтому принимаем решение выдать клиенту ссуду. Сумма 1560 долл. надписывается над квадратом 4, а альтернативная «ветвь» перечеркивается. Теперь вернемся к «узлам» А и 1. Используя ожидаемые чистые доходы над квадратами 2 и 3, рассчитаем математическое ожидание для кружка А: M (А) = (1905 долл. х 0,75) + (1350 долл. х 0,25) = 1766 долл. Так как аудиторская проверка стоит 80 долл., ожидаемый чистый доход составит: NM (А) = 1766 - 80 = 1686 долл. Теперь можно проставить значения первого решения квадрата 1. Должен ли банк воспользоваться аудиторской проверкой? В этом «узле» максимальное математическое ожидание — 1686 долл., поэтому перечеркиваем альтернативную «ветвь». На рис. ниже стрелками показана последовательность решений, ведущая к максимальному чистому доходу: в квадрате 1 воспользуемся аудиторской проверкой. Если выдача займа рекомендуется фирмой, тогда в квадрате 2 — выдать ссуду, если не рекомендуется, то в квадрате 3 — не выдавать ссуду, а инвестировать эти деньги под стабильные 9% годовых. 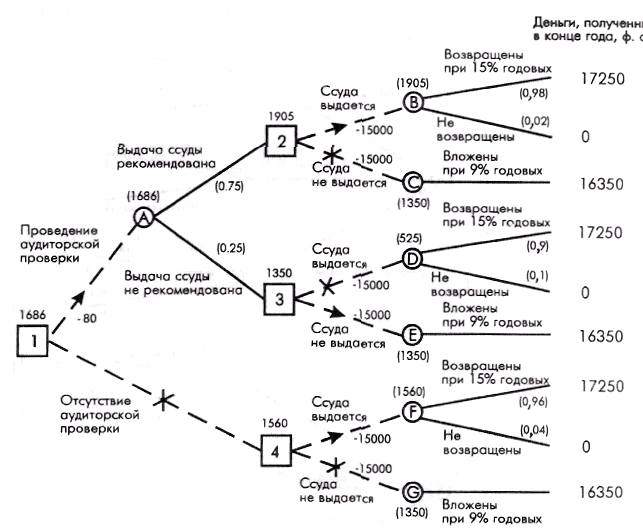 Построение индивидуальной функции полезности. В предыдущих примерах платежи выражались в виде реальных денег. Зачастую возникают ситуации, когда при анализе следует использовать скорее «полезность», чем реальную величину платежей. Для демонстрации этого предположим следующее. Существует шанс 50 на 50, что инвестиция в 20 000 долл. или принесет прибыль в 40 000 долл., или будет полностью потеряна. Соответствующая ожидаемая прибыль равна 40 000 х 0,5 – 20 000 х 0,5 = 10000 долл. Хотя ожидается прибыль в виде чистого дохода, разные люди могут по-разному интерпретировать полученный результат. Инвестор, который идет на риск (или миллионер), может вложить деньги, чтобы с вероятностью 50 % получить прибыль в 40 000 долл. Наоборот, осторожный инвестор (студент?) может не захотеть рисковать потерей 20 000 долл. Определение полезности является субъективным. Оно зависит от нашего отношения к риску. Рассмотрим, как можно построить функцию полезности отражающую наше отношение к деньгам, например, к риску выиграть или проиграть определенную сумму. В примере, приведенном выше, наилучший платеж равен 40 000 долл., а наихудший (–20 000) долл. Мы устанавливаем шкалу полезности U (utility), изменяющуюся от 0 до 100, где 0 соответствует полезности –20 000, а 100 — 40000, т.е. U(–20000) = 0 и U(40000) = 100. Разумеется, 0 и 100 как границы шкалы выбраны произвольно Если отношение ЛПР беспристрастно к риску, то результирующая функция полезности является прямой линией, соединяющей точки (0, –20000) и (100, 40000). В этом случае полезность равна денежной оценке результата. В более реальных ситуациях функция полезности может принимать другой вид. Ниже на рисунке иллюстрируется вид функции полезности для трех индивидуумов X, Y и Z. X осторожен и не склонен к риску, так как проявляет большую чувствительность к потере, чем к прибыли. Это следует из того, что для индивидуума X при изменении в 10 000 долл. вправо и влево от точки, соответствующей 0 долларов, увеличение прибыли изменяет полезность на величину ab, которая меньше изменения полезности bс, обусловленной потерями такой же величины, т.е. ab < bс. Z, наоборот, настроен на риск. Такие же изменения в ±10 000 долл., обнаруживают противоположное поведение; здесь de > ef. А индивидуум Y является нейтральным к риску, так как упомянутые изменения порождают одинаковые изменения полезности. В общем случае индивидуум может быть, как не расположен к риску, так и настроен на риск, в зависимости от суммы риска. В этом случае соответствующая кривая полезности будет иметь вид удлиненной буквы S. 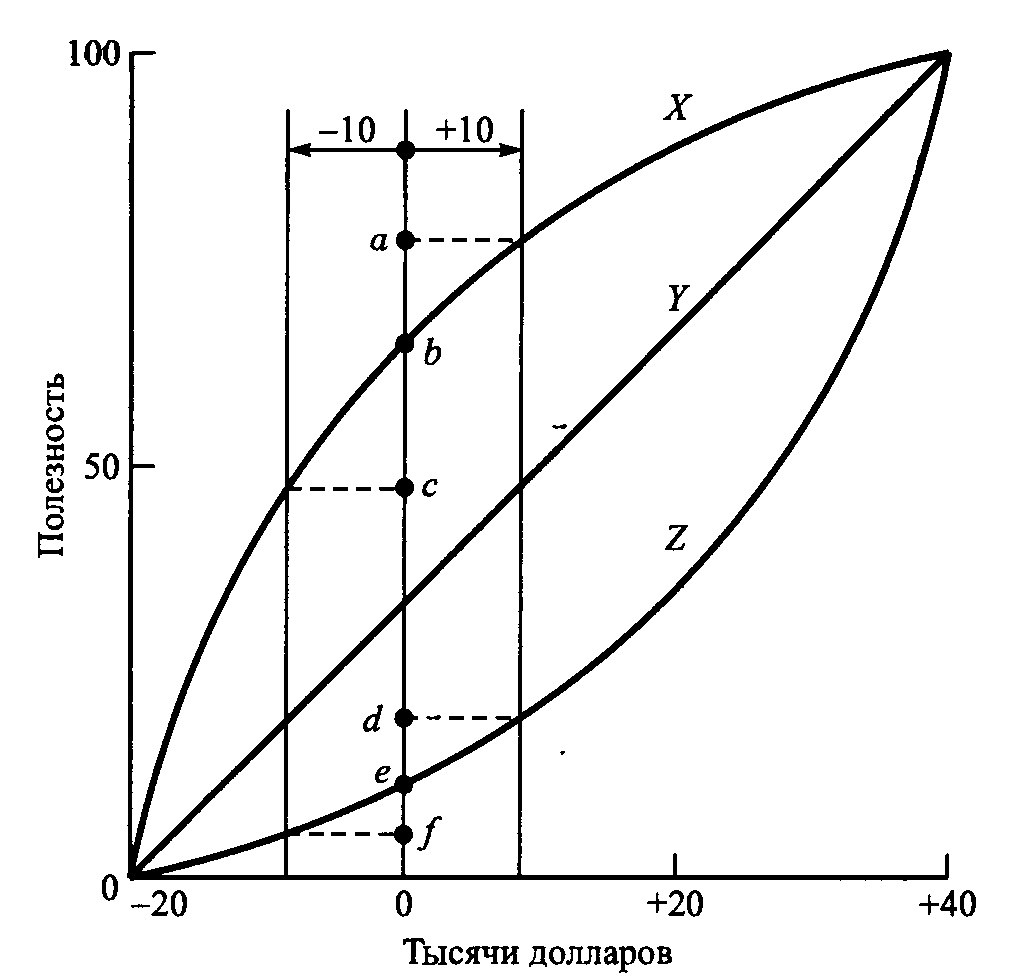 Определим теперь полезность, соответствующую промежуточным значениям платежей, например, –10 000, 0, 10 000, 20 000 или 30 000. Для определения полезности суммы реальных денег х, будем использовать такую формулу U(x) = p*U(-20000) + (1-p)*U(40000) = 100*(1-p), 0 Для определения значения U(x) просят ЛПР сообщить свое предпочтение между гарантированной наличной суммой х и возможностью сыграть в лотерею, в которой с вероятностью р реализуется проигрыш в сумме 20000 долл. и с вероятностью 1-р имеет место выигрыш в 40000 долл. Под предпочтением понимается выбор значения «нейтральной» вероятности р, при котором, с точки зрения лица, принимающего решение, возможности сыграть в лотерею или получить гарантированную сумму х являются одинаково привлекательными. Например, если х = 10000 долл., лицо, принимающее решение, может заявить, что гарантированные 10000 долл. наличными и лотерея одинаково привлекательны при р = 0,3. В этом случае вычисляется полезность для х = 10000 по следующей формуле. U(10000) = 100*(1 - 0,3) = 70. Эта процедура продолжается до тех пор, пока не будет получено достаточное количество точек (х, U(х)) для определения формы функции полезности. Затем можно определить U(х) путем интерполяции между полученными точками. Задания
Задача 1 Вас пригласили на телевизионную игру «Колесо фортуны». Колесо управляется с помощью двух кнопок, которые сообщают ему сильное (В) или слабое (Н) вращение. Само колесо разделено на равные области — белую (Б) и черную (Ч). Вам сообщили, что в белой области колесо останавливается с вероятностью 0,3, а в черной — 0,7. Плата, которую вы получаете за игру, равна (в долл.) следующему. Построить дерево решений. Каково ожидаемое значение прибыли?
Задача 2 Фермер может выращивать либо кукурузу, либо соевые бобы. Вероятность того, что цены на будущий урожай этих культур повысятся, останутся на том же уровне или понизятся, равна соответственно 0,25, 0,30 и 0,45. Если цены возрастут, урожай кукурузы даст 30 000 долл. чистого дохода, а урожай соевых бобов — 10 000 долл. Если цены останутся неизменными, фермер лишь покроет расходы. Но если цены станут ниже, урожай кукурузы и соевых бобов приведет к потерям в 35 000 и 5 000 долл. соответственно. Постройте дерево решений. Какую культуру следует выращивать фермеру? Каково ожидаемое значение его прибыли? Задача 3 Фирма планирует открыть новое предприятие в Арканзасе. В настоящее время имеется возможность построить либо крупное предприятие, либо небольшое, которое через два года можно будет расширить при условии высокого спроса на выпускаемую им продукцию. Рассматривается задача принятия решений на десятилетний период. Фирма оценивает, что на протяжении этих 10 лет вероятность высокого и низкого спроса на производимую продукцию будет равна 0,75 и 0,25 соответственно. Стоимость немедленного строительства крупного предприятия равна 5 млн. долл., а небольшого — 1 млн. долл. Расширение малого предприятия через два года обойдется фирме в 4,2 млн. долл. Прибыль, получаемая от функционирования производственных мощностей на протяжении 10 лет, приводится в следующей таблице.
Постройте соответствующее дерево решений, принимая во внимание, что через два года фирма может либо расширить небольшое предприятие, либо не расширять его. Сформулируйте стратегию строительства для фирмы на планируемый 10-летний период. (Для простоты не принимайте во внимание возможную инфляцию.) Задача 4 Допустим, у вас имеется возможность вложить деньги в три инвестиционных фонда открытого типа: простой, специальный (обеспечивающий максимальную долгосрочную прибыль от акций мелких компаний) и глобальный. Прибыль от инвестиции может измениться в зависимости от условий рынка. Существует 10%-ная вероятность, что ситуация на рынке ценных бумаг ухудшится, 50%-ная — что рынок останется умеренным и 40%-ная — что рынок будет возрастать. Следующая таблица содержит значения процентов прибыли от суммы инвестиции при трех возможностях развития рынка. Постройте дерево решений. Какой фонд открытого типа вам следует выбрать? Какой процент прибыли при этом ожидается?
Задача 5 Предположим, у вас имеется возможность вложить деньги либо в 7,5%-ные облигации, которые продаются по номинальной цене, либо в специальный фонд, который выплачивает лишь 1% дивидендов. Если существует вероятность инфляции, процентная ставка возрастет до 8%, и в этом случае номинальная стоимость облигаций увеличится на 10%, а цена акций фонда — на 20%. Если прогнозируется спад, то процентная ставка понизится до 6%. При этих условиях ожидается, что номинальная стоимость облигаций поднимется на 5%, а цена акций фонда увеличится на 20%. Если состояние экономики останется неизменным, цена акций фонда увеличится на 8%, а номинальная стоимость облигаций не изменится. Экономисты оценивают в 20% шансы наступления инфляции и в 15% — наступление спада. Ваше решение относительно инвестиций принимается с учетом экономических условий следующего года. Представьте задачу в виде дерева решений. Будете ли вы покупать акции фонда или облигации? Какая прибыль при этом ожидается? Задача 6 Издатель обратился в отдел маркетинга, чтобы выяснить предполагаемый спрос на книгу. Исследования отдела маркетинга показали:
Прибыль от продажи составляет 9 ф. ст. за книгу. Если книга не продается, убытки составляют 4 ф. ст. за штуку. Если издатель не удовлетворяет спрос, убытки по неудовлетворенному спросу составят 1 ф. ст. (для поддержания репутации фирмы и будущего спроса). Определите, сколько должно быть издано книг в расчете на трехлетний период. Задача 7 Фирма планирует производство новой продукции быстрого питания в национальном масштабе. Исследовательский отдел убежден в большом успехе новой продукции и хочет внедрить ее немедленно, без рекламной кампании на рынках сбыта фирмы. Отдел маркетинга положение вещей оценивает иначе и предлагает провести интенсивную рекламную кампанию. Такая кампания обойдется в 100 тыс. долл., а в случае успеха принесет 950 тыс. долл. годового дохода. В случае провала рекламной кампании (вероятность этого составляет 30%) годовой доход оценивается лишь в 200 тыс. долл. Если рекламная кампания не проводится вовсе, годовой доход оценивается в 400 тыс. долл. при условии, что покупателям понравится новая продукция (вероятность этого равна 0,8), и в 200 тыс. долл. с вероятностью 0,2, если покупатели останутся равнодушными к новой продукции. Постройте соответствующее дерево решений. Как должна поступить фирма в связи с производством новой продукции? Задача 8 Небольшая химическая фирма «Hetros Hetrosone Ltd» выпускает дорогой промышленный растворитель «Hetrosone», который быстро портится. Поэтому запасы «Hetrosone» нельзя держать больше, чем один месяц. Объемы выпуска продукции планируются в начале каждого месяца, и под эти планы закупается необходимое сырье. Продажная цена «Hetrosone» — 2400 ф. ст. за 1 т, производственные расходы — 1500 ф. ст. за 1 т. Анализируя спрос за последние несколько месяцев, менеджер по сбыту установил, что спрос колеблется между 10 и 20 т в месяц. Для того чтобы упростить анализ спроса, он подразделил его на три типа — «низкий» (10 т), «средний» (15 т) и «высокий» (20 т) с соответствующими вероятностями:
Учитывая уровни спроса, составьте «дерево» решений, охватывающее все возможности, открывающиеся перед компанией, а также их исходы. Предположим, уровни спроса не изменяются. Какой объем производства вы бы могли посоветовать, чтобы максимизировать прибыль в долгосрочной перспективе? Задача 9 Пекарня печет хлеб на продажу магазинам. Себестоимость одной булки составляет 30 пенсов, ее продают за 40 пенсов. В таблице приведены данные о спросе за последние 50 дней:
Если булка испечена, но не продана, то убытки составят 20 пенсов за штуку. Определите, сколько булок нужно выпекать в день. Задача 10 Фирма производит партии продукции с 0,8, 1, 1,2 и 1,4 % бракованных изделий с вероятностями 0,4, 0,3, 0,25 и 0,05 соответственно. Три потребителя А, В и С заключили контракт на получение партий изделий с процентом некачественных изделий не выше 0,8, 1,2 и 1,4% соответственно. Фирма штрафуется в сумме 1000 долл. за каждый пункт процента (одна десятая процента) в случае, если процент некачественных изделий выше указанного. Наоборот, поставка партий изделий с меньшим процентом бракованных изделий, чем оговорено в контракте, приносит фирме прибыль в 500 долл. за каждый пункт процента. Предполагается, что партии изделий перед отправкой не проверяются. Постройте соответствующее дерево решений. Какой из потребителей должен иметь наивысший приоритет при получении своего заказа? Задача 11 Ежедневный спрос на булочки в продовольственном магазине задается следующим распределением вероятностей.
Магазин покупает булочку по 55 центов, а продает по 1,20 долл. Если булочка не продана в тот же день, то к концу дня она может быть реализована за 25 центов. Величина запаса булочек может принимать одно из возможных значений спроса, которые перечислены выше. Постройте соответствующее дерево решений. Сколько булочек необходимо заказывать ежедневно? Задача 12 Компания «Brownhill Manufacturing Company» собирается производить новый товар, для чего нужно будет построить новый завод. После рассмотрения нескольких вариантов были оставлены три основных. А. Построить завод стоимостью 600000 ф. ст. При этом варианте возможны: большой спрос с вероятностью 0,7 и низкий спрос с вероятностью 0,3. Если спрос будет большим, то ожидается годовой доход в размере 250000 ф. ст. в течение следующих пяти лет; если спрос низкий, то ежегодные убытки из-за больших капиталовложений составят 50000 ф. ст. Б. Построить маленький завод стоимостью 350000 ф. ст. Здесь также возможны большой спрос с вероятностью 0,7 и низкий спрос с вероятностью 0,3. В случае большого спроса ежегодный доход в течение пяти лет составит 150000 ф. ст., при низком спросе — 25000 ф. ст. В. Сразу завод не строить, а отложить решение этого вопроса на один год для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностями 0,8 и 0,2 соответственно. Через год, если информация окажется позитивной, можно построить большой или маленький завод по указанным выше ценам. Руководство компании может решить вообще никакого завода не строить, если информация будет негативной. Вне зависимости от типа завода вероятности большого и низкого спроса меняются на 0,9 и 0,1 соответственно, если будет получена позитивная информация. Доходы на последующие четыре года остаются такими же, какими они были в вариантах А и Б. Все расходы выражены в текущей стоимости и не должны дисконтироваться. Нарисуйте «дерево», охватывающее все возможности, открывающиеся перед компанией. Определите наиболее эффективную последовательность действий руководства фирмы, основываясь на ожидаемых доходах каждого варианта. Литература Таха Х. Введение в исследование операций. — М.: Вильямс, 2005. — 912 с. Эддоус М., Стэнсфилд Р. Методы принятия решений. — М.: Аудит, ЮНИТИ, 1997. — 590 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
