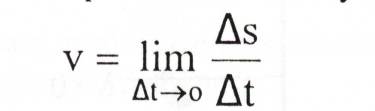Раздел. Раздел I.Механика Текст. Природа это храм, где камни говорят
 Скачать 1.19 Mb. Скачать 1.19 Mb.
|
|
Скалярные величины – величины, характеризующиеся числовым значением (t¸ m). Векторные величины – величины, характеризующиеся числовым значением и направлением ( 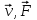 ). ).Сложение векторов. Вектора складываются по правилам: 1) параллелограмма – расположить вектора 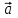 и и 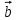 так, чтобы они выходили из одной точки, достроить до параллелограмма; диагональ, исходящая из начальной точки и является суммой этих векторов; так, чтобы они выходили из одной точки, достроить до параллелограмма; диагональ, исходящая из начальной точки и является суммой этих векторов; 2) треугольника – из конца вектора 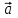 отложить вектор отложить вектор 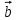 ; вектор, соединяющий начало вектора ; вектор, соединяющий начало вектора 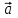 и конец вектора и конец вектора 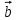 , является суммой этих векторов. , является суммой этих векторов. 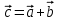 Математические действия с векторами производятся геометрически. Если вектора параллельны, то они складываются аналогично. По модулю результирующий вектор равен арифметической сумме (если в одну сторону), либо арифметической разности (если в разные стороны). Направлен результирующий вектор либо в ту же сторону, что и складываемые векторы, либо в сторону большего по модулю вектора. Проекцией вектора 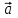 на ось Х называется отрезок на ось Х называется отрезок 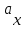 между проекциями на эту ось начала и конца вектора. Если проекция вектора на ось совпадает с положительным направлением оси, то она положительна. В противном случае проекция вектора отрицательна. Если вектор перпендикулярен оси, то его проекция на ось равна нулю. между проекциями на эту ось начала и конца вектора. Если проекция вектора на ось совпадает с положительным направлением оси, то она положительна. В противном случае проекция вектора отрицательна. Если вектор перпендикулярен оси, то его проекция на ось равна нулю.Проекция вектора на ось – скаляр, поэтому математические действия с проекциями производятся алгебраически. Если известен вектор перемещения, то известна и его проекция на координатную ось (или оси). Рассмотрим это на примере. Пусть тело совершило перемещение 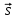 , где ( , где (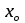 , ,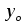 ) – начало перемещения, (x,y) – конец перемещения. ) – начало перемещения, (x,y) – конец перемещения. 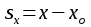 Тогда: - проекция вектора 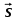 на ось Х на ось Х 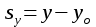 - проекция вектора 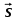 на ось Y на ось YПроекция вектора перемещения 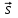 на оси координат X и Y равны изменениям координат тела x и y. на оси координат X и Y равны изменениям координат тела x и y.Зная вектор перемещения, можно узнать и координаты тела x и y: 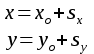 Модуль вектора перемещения равен 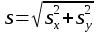 Если треугольник не прямоугольный, то одну из сторон можно найти по теореме косинусов: a2= b2 + c2 – 2bс cos α ОК – 3 Равномерное прямолинейное движение любые t равные s Всплывает пузырек, тонут тела, опускается парашют.  Время – t – с 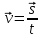 ℓ=s (?!) ℓ=s (?!)  Модуль перемещения – s –м 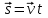 Модуль скорости – υ – м/с  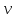 x = x =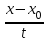 36 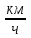 = = 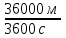 = 10 = 10 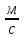 спидометр спидометр физич. смысл скорости:  уравнение координаты x = x0 + υxt уравнение координаты x = x0 + υxtПроекция скорости 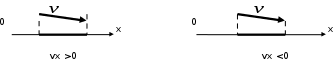 График скорости График координаты 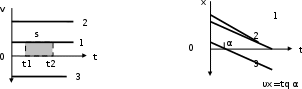   v2 > v1 v2 > v1v3 < 0 s = v1· (t2 – t1) Равномерное прямолинейное движение – движение, при котором тело за любые одинаковые промежутки времени совершает равные перемещения. Например, всплывает пузырек газа в стакане газированной воды, тонут тела, опускается парашютист с раскрытым парашютом. Для количественной характеристики процесса движения тела вводится понятие скорости движения. Скоростью равномерного прямолинейного движения называют величину, равную отношению перемещения тела к промежутку времени, в течение которого это перемещение произошло. Для нахождения скорости тела(υ) надо знать пройденный им путь (s) и разделить его на время движения (t): 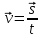 . Скорость – векторная величина, то есть имеет направление. При равномерном движении скорость тела остается постоянной. . Скорость – векторная величина, то есть имеет направление. При равномерном движении скорость тела остается постоянной.Зная скорость равномерного движения, можно найти путь, пройденный за любой промежуток времени, по формуле 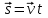 . Направлен вектор скорости так же, как вектор перемещения. Направление вектора скорости – это и есть направление движения тела. Так как движение прямолинейное, то пройденный путь и модуль перемещения равны. . Направлен вектор скорости так же, как вектор перемещения. Направление вектора скорости – это и есть направление движения тела. Так как движение прямолинейное, то пройденный путь и модуль перемещения равны.В Международной системе (СИ) единицей расстояния является метр, единицей времени – секунда; поэтому скорость выражается в метрах в секунду: 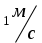 . Скорость тела можно измерять также в километрах в час ( . Скорость тела можно измерять также в километрах в час (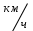 ); километрах в секунду ( ); километрах в секунду (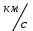 ) и др. Рассмотрим, как переводят ) и др. Рассмотрим, как переводят 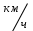 в в 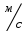 : 36 : 36 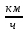 = = 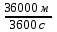 = 10 = 10 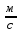 . Скорость движения транспортных машин измеряется прибором – спидометром, где числа шкалы показывают скорость, выраженную в . Скорость движения транспортных машин измеряется прибором – спидометром, где числа шкалы показывают скорость, выраженную в 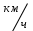 . . Скорость – векторная величина – имеет направление. Направление скорости совпадает с направлением движения. Скорость может быть постоянной, а может быть переменной Единицы измерения скорости В СИ: [v] = [1 м/с] Кратные: 1 км/ч = 3,6 м/с; 1 км/с = 1000 м/с Дольные: 1 см/с = 0,1 м/с; 1 дм/с = 0,1 м/с  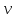 x = x =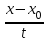 Физический смысл скорости:скорость характеризует быстроту изменения координаты в единицу времени. При этом, необходимо помнить, что проекция скорости υx может быть как положительной, так и отрицательной. Уравнение координат имеет следующий вид: x = x0 + υxt . Данное уравнение показывает, как координата х тела зависит от времени t. А это и есть решение основной задачи механики. График скорости показывает, как изменяется скорость с течением времени. Его получают, откладывая по оси абсцисс время, а по оси ординат – проекции скорости тела. График скорости представляет собой прямую, параллельную оси времени. Чем выше график, тем больше скорость тела. Графики 1 и 2 относятся к случаю, когда проекция скорости >0, график 3 – когда проекция <0. Перемещение тела за данный промежуток времени численно равно площади закрашенного прямоугольника. График координаты показывает, как изменяется координата с течением времени. Его получают, откладывая по оси абсцисс время, а по оси ординат – координаты тела. Координата линейно зависит от времени. Чем круче график движения, тем больше скорость (υx=tq α). Графики 1 и 3 соответствуют движению тела сонаправленно с осью Х, график 2 – в противоположном направлении. Начальная координата графика 1 равна нулю. У графика 2 координата в начальный момент времени х0>0, у графика 3 х0<0. ОК – 4 Относительность движения
 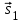 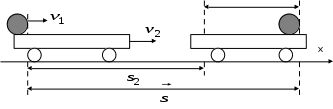 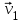 - скорость тела относительно подвижной системы отсчета, - скорость тела относительно подвижной системы отсчета,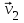 - скорость подвижной системы отсчета относительно неподвижной системы отсчета, - скорость подвижной системы отсчета относительно неподвижной системы отсчета,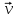 - скорость тела относительно неподвижной системы отсчета. - скорость тела относительно неподвижной системы отсчета.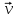 = =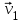 + +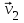 (классический закон сложения скоростей) (классический закон сложения скоростей)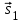 - перемещение тела относительно подвижной системы отсчета, - перемещение тела относительно подвижной системы отсчета,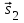 - перемещение подвижной системы отсчета относительно неподвижной системы отсчета, - перемещение подвижной системы отсчета относительно неподвижной системы отсчета,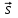 - перемещение тела относительно неподвижной системы отсчета. - перемещение тела относительно неподвижной системы отсчета.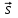 = =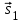 + +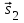
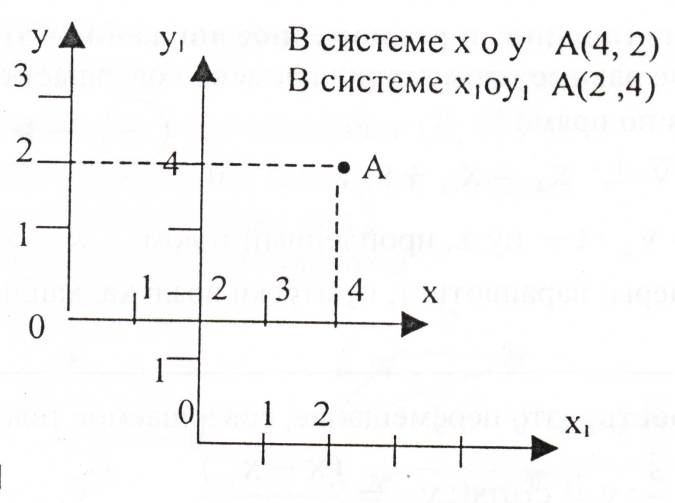
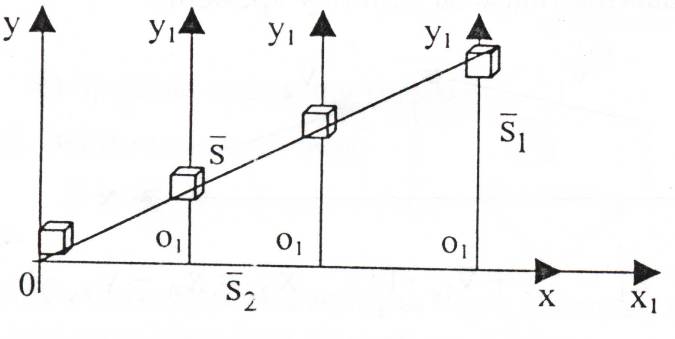
Принцип относительности Галилея: Все ИСО равноправны: ход времени, масса, ускорение и сила в них записываются одинаково. Скорости и перемещения связаны правилами сложения этих величин. Положение тела различно относительно разных систем координат: в системе хоу А(4, 2), а в системе х1оу1 А(2,4). Абсолютного покоя в природе не существует. Если тело находится в покое относительно другого, то всегда можно найти такие тела, относительно которых оно движется. Например, человек сидит в движущемся автобусе. Относительно автобуса человек находится в состоянии покоя, а относительно домов, деревьев – движется. Движение тела различно относительно разных систем координат. То, что характер данного движения тела оказывается различным относительно разных тел, называют относительностью движения. Всякое движение, а также покой тела относительны. При изучении движений на поверхности Земли обычно принимают за систему отсчета Землю. Рассмотрим, как связаны между собой скорости движения тела в различных системах отсчета. Рассмотрим такой пример. Тележка движется по прямолинейному участку пути равномерно со скоростью 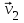 относительно Земли. Мяч движется относительно тележки со скоростью относительно Земли. Мяч движется относительно тележки со скоростью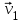 . Скорость мяча относительно Земли равна . Скорость мяча относительно Земли равна 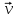 = =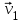 + +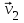 . Закон, выражаемый данной формулой, называется классическим законом сложения скоростей. . Закон, выражаемый данной формулой, называется классическим законом сложения скоростей.Перемещение мяча относительно Земли находиться по формуле: 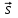 = =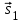 + +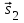 , ,где 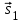 - перемещение мяча относительно движущейся тележки, - перемещение мяча относительно движущейся тележки, 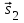 - перемещение тележки относительно Земли. - перемещение тележки относительно Земли.Рассмотрим другой пример. Система хоу является неподвижной, система х1оу1 движется относительно системы хоу со скоростью v2, перпендикулярно оси ох1 движется кубик со скоростью v1. Кубик переместился на 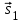 , система х1оу1 на , система х1оу1 на 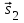 . Перемещение и скорость кубика относительно системы хоу находятся по формулам: . Перемещение и скорость кубика относительно системы хоу находятся по формулам: 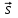 = =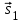 + +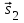 и и 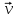 = =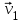 + +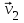 . Если кубик будет двигаться не перпендикулярно оси ох, а под некоторым углом, то формулы будут такие же. . Если кубик будет двигаться не перпендикулярно оси ох, а под некоторым углом, то формулы будут такие же.Перемещение тела и перемещение системы складываются векторно; скорость тела и скорость системы отсчета складываются векторно. Если мы будем производить разные механические опыты в вагоне поезда, идущего равномерно по прямолинейному участку пути, а затем повторим те же опыты на земной поверхности, то убедимся, что они будут совершено одинаковые. В ИСО невозможно отличить покой от равномерного прямолинейного движения. Для любых механических явлений все ИСО оказываются равноправными. Это впервые установил Г.Галилей и называется по его имени. Принцип относительности Галилея: Все ИСО равноправны: ход времени, масса, ускорение и сила в них записываются одинаково. Скорости и перемещения связаны правилами сложения этих величин. ОК – 5 Неравномерное прямолинейное движение (переменное) … любые t неравные … s Средняя скорость – весь путь ко всему времени. 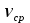 = =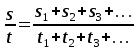
Неравномерное прямолинейное движение – движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения. При неравномерном движении нельзя говорить о какой – то определенной скорости, так как отношение пройденного пути к соответственному промежутку времени не одинаково для разных участков. Если, однако, нас интересует движение только на каком-либо определенном участке пути, то это движение в целом можно охарактеризовать, введя понятие средней скорости движения. Средняя скорость – отношение длины данного участка к промежутку времени, за который этот участок пройден. В общем случае средняя скорость не равна среднему значению от средних скоростей на отдельных участках пути. Для описания неравномерного движения можно определить среднюю скорость движения на нескольких участках пути. Однако это даст лишь грубое, приближенное понятие о характере движения. Для более точного описания движения необходимо измерять средние скорости за малые промежутки времени. Среднюю скорость, измеренную за столь малый промежуток времени, что движение можно считать равномерным, называют мгновенной скоростью. Мгновенная скорость равномерного движения постоянна. Мгновенная скорость неравномерного движения – переменная величина, принимающая различные значения в разные моменты времени. |