отопение. микро макро экономика. Процентная ставка, Спрос на деньги (ден ед.)
 Скачать 108.36 Kb.
|
|
Реальный ВНП в экономике 6000 ден. ед., уровень цен – 3; денежная единица совершает 9 оборотов в год. Зависимость спроса на деньги от процентной ставки представлена в таблице. Нарисуйте графики трансакционного, спекулятивного и общего спроса на деньги.
Технология решения задачи: Сначала определим трансакционный спрос на деньги по формуле:  Подставив значения, получаем: 3 * 6000: 9 = 2000 ден. ед. График трансакционного спроса на деньги будет представлять собой вертикальную прямую:  График спекулятивного спроса на деньги строится по точкам, исходя из зависимости спроса от процентной ставки, данной в таблице, т. е. при 15 % ставке спроса на деньги как финансовый актив предъявляться не будет. Чем ниже ставка, тем больше потребность, поэтому график будет представлять собой нисходящую прямую. 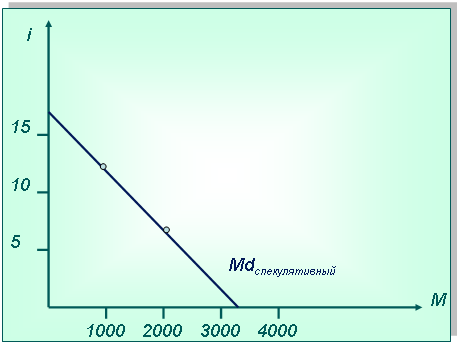 Общий спрос на деньги определяется как сумма транcакционного спроса и спекулятивного спроса, т. е. при ставке 15 % — 2000 + 0 = 2000, при ставке 10 % — 2000 + 1000 = 3000 и т. д. График общего спроса также складывается из графиков трансакционного и спекулятивного спроса: 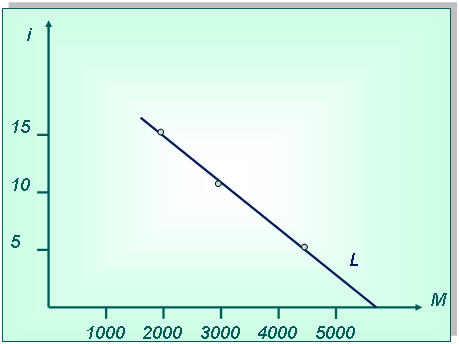 2. Постановка задачи: Реальный ВНП в экономике 50 000 ден. ед., уровень цен - 3; денежная единица совершает 7,5 оборота в год. Зависимость спроса на деньги от процентной ставки представлена в таблице:
Определите, при какой ставке процента на денежном рынке установится равновесие и как она изменится, если денежная масса в экономике уменьшится с 31 000 до 28 000 ден. ед. Технология решения задачи: Сначала определяется спрос на деньги для сделок по формуле: Р * ВНП/v, т. е. 3*50000:7,5=20000 ден. ед. Так как предложение денег (денежная масса) первоначально было равно 31 000 ден. ед., то на обеспечение спекулятивного спроса оставалось 11 000 ден. ед. Следовательно, при ставке 6 % устанавливалось первоначальное равновесие на денежном рынке. Уменьшение денежной массы привело к сокращению доступных для спекулятивных нужд средств до 8000 ден. ед. Вследствие этого процентная ставка увеличилась до 8 %, и равновесие на денежном рынке восстановилось. Ответ: увеличится с 6 до 8 %. 3. Постановка задачи: Предложение денег осуществляется по формуле  . Спекулятивный спрос на деньги определяется формулой  . Годовой ВНП составляет 8400 у. е., уровень цен равен 1, скорость оборота денежной единицы 12 оборотов в год. Определите равновесную ставку процента.Технология решения задачи: Сначала определяется спрос на деньги для сделок по формуле  . Подставив значения, получим:  у. е. Затем найдем общий спрос на деньги, сложив трансакционный и спекулятивный спрос:  . Теперь найдем равновесие на денежном рынке: Мs = L, т. е. 45+150i=725–60i. Следовательно, при ставке 3 установится равновесие на денежном рынке.Ответ: i = 3. 4. Постановка задачи: Рассмотрим закрытую экономику, которая характеризуется следующими данными: С = 170 + 0,6Yv; Inv = 100 – 40i; G = 350; T = 200; L = 0,75Y – 6i; Ms = 735. Выведите формулу IS. Технология решения задачи: Формула имеет вид  .Подставив значения в формулу, получим:  , отсюда ,  .Ответ: IS: i = 12,5 – 0,01Y. 5. Постановка задачи: Рассмотрим закрытую экономику, которая характеризуется следующими данными: С = 170 + 0,6Yv; Inv = 100 – 40i; G = 350; T = 200; L = 0,75Y – 6i; Ms = 735. Определите равновесную ставку процента и эффективный спрос. Технология решения задачи: Выведем формулу IS: .IS: Y = 170 + 0,6(Y – 200) + 100 – 20i + 350= 0,6Y – 20i + 500, отсюда 0,4Y – 500 = 20i; IS: i = 12,5 – 0,01Y. Затем определим кривую LM.  . Подставив значения в формулу, получим:LM: 0,75Y – 6i = 735, отсюда 6i = 0,75 – 735, LM: i = 0,125Y + 122,5. Решив систему уравнений, получим равновесную процентную ставку 2,5 и эффективный спрос Y = 1000. Ответ: равновесная ставка процента 2,5; эффективный спрос 1000. 6. Постановка задачи: Состояние экономики характеризуется следующими параметрами: С = 0,5Yv + 80, Inv = 300 – 10i, G = 0,1Y + 60, налоги составляют 100 у. е., Ms = 500, L = 0,4Y + 100 – 12i. Используя модель IS – LM, определите параметры совместного равновесия. Технология решения задачи: Модель IS - LM состоит из двух кривых, уравнения которых: 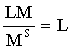; . Подставив значения в формулы, получим:IS: Y = 0,5(Y – 100) +80 + 300 – 10i + 0,1Y + 60 = 0,6Y – 10i + 390, LM: 0,4Y +100 – 12i = 500 или IS: 0,4Y = 390 – 10i, LM: 0,4Y = 400 – 12i. Решив систему уравнений, получим равновесную процентную ставку i = 5. Подставив ее в уравнение любой кривой, получим: Y = 850. Ответ: равновесный ВНП = 850, равновесная процентная ставка 5. 7. Постановка задачи: На основе следующих данных определите эффективный спрос: С = 0,6Y + 50; Inv = 200 – 20i; Mdсд = 0,5Y; Mdим = 500 – 50i; Ms = 400. Технология решения задачи: Для решения используется модель IS – LM, уравнения которой: ; . Подставив значения в формулы, получим:IS: Y = 0,6Y + 50 + 200 – 20i = 0,6Y – 20i + 250; LM: 0,5Y +500 – 50i = 400. Решив уравнения, получим равновесную процентную ставку 16,5 и эффективный спрос Y = 1450. Ответ: 1450 у. е. 8. Постановка задачи: Спрос населения на деньги определяется формулой L = 0,8Y + 600 – 50i. В обращении находится 1000 ден. ед. Уровень цен равен 1. Инвестиционный спрос предпринимателей представлен функцией Inv = 80 – 10i, потребительский спрос определяется как: С = 1200 + 0,6Yv. Государственные расходы на ВНП равны налогам и равны 500 ден. ед. Как изменится равновесная ставка процента и равновесный ВНП, если количество денег в обращении сократится на 100 ден. ед. Технология решения задачи: Задача решается путем определения уравнений кривых IS, LM: ; . Подставив значения в формулы, получим:IS: Y = 0,6(Y – 500) + 1200 + 80 – 10i + 500 = 0,6Y – 10i + 1480; LM: 0,8Y + 600 – 50i = 1000; IS: i = 148 – 0,04Y; LM: i = 0,016Y – 8. Решив уравнения, получим равновесную процентную ставку 36,57 и эффективный спрос Y = 2785,7. Если количество денег уменьшится, то LM приобретет другой вид: 0,8Y + 600 – 50i = 900 или LM: I = 0,016Y – 6. Решим уравнения модели IS – LM, в результате получим процентную ставку 38 и ВНП = 2750 ден. ед. Таким образом, процентная ставка вырастет на 1,43, а ВНП сократится на 35,7 ден. ед. Ответ: процентная ставка вырастет на 1,43, а ВНП сократится на 35,7 ден. ед. 9. Постановка задачи: В закрытой экономике без участия государства потребление определяется функцией С = 0,75Y + 60, инвестиции – Inv = 200 – 5i. Спрос на деньги как имущество задан формулой Мdим. = 200 – 10i, спрос на деньги для сделок Мdсд. = 0,5Y. В обращении находится 450 ден. ед. Определите равновесные значения процентной ставки и ВНП и их изменение, если увеличится предельная склонность к потреблению до 0,8. Технология решения задачи: Находим первоначальное равновесие, используя уравнения кривых IS и LM. Так как государство и заграничный сектор отсутствует, то можно вывести функцию сбережений и ее формулу приравнять к формуле инвестиций: IS: Inv = S; 200 – 5i = 0,25Y – 60; Y = 1040 – 20i; LM: 0,5Y = 10i – 300; Y = 20i – 300. Решив систему уравнений, получаем равновесную процентную ставку, равную 18,5, и равновесный ВНП – 670 ден. ед. Если изменится функция потребления, то изменится и функция сбережения. В результате уравнение кривой IS будет выглядеть так: IS: 200 – 5i = 0,2Y – 60; Y = 1300 – 25i; LM: Y = 20i – 300. Решив уравнения, получаем: i = 22,2; ВНП = 743 ден. ед., т. е. произошло увеличение процентной ставки и ВНП. Ответ: процентная ставка увеличилась с 18,5 до 22,2; ВНП вырос с 670 до 743 ден. ед. |