Реферат на тему: Процессы теплопередачи при рафинировании хрома. теплопередача. Процессы теплопередачи при рафинировании хрома
 Скачать 0.66 Mb.
|
Процессы теплопередачи при рафинировании хрома2.1. Теплопроводность и теплопередачаСегодня практически любая область инженерной деятельности во многом связана с проблемами энергосбережения, разработкой, внедрением и эксплуатацией ресурсосберегающих технологий, с вопросами трансформации и передачи энергии. Учебная дисциплина "Теоретические основы теплотехники" призвана вооружить будущего специалиста знаниями общих законов и основанных на этом инженерных методик расчета процессов, возникающих при получении, трансформации и распространении в пространстве тепловой энергии. Структурно сюда входят две отдельные науки: "Термодинамика" и "Теплопередача". Термодинамика изучает законы превращения различных видов энергии в тепло (и наоборот – тепла в другие виды энергии), а также особенности физических процессов, сопровождающих эти превращения. Как самостоятельная наука термодинамика начала складываться в начале XIX века, хотя многие принципиальные ее положения были открыты и сформулированы еще ранее в рамках общефизической теории. Среди основоположников и ученых, внесших наибольший вклад в развитие термодинамики, мы встречаем известные имена: М. В. Ломоносова, который в работе "Размышления о причинах тепла и холода" (1744 г.) предложил единую теорию теплоты и строения вещества, сформулировав законы сохранения массы и энергии, Д. Джоуля, В. Томсона, Р. Клаузиуса, С. Карно, Г. Гесса, Л. Больцмана, Н. В. Гиббса, М. П. Вукаловича, А. А. Гухмана и др. Подробно об истории развития термодинамики и вклад отдельных ученых в эту науку можно прочитать в интересной книге [1]. За более чем стопятидесятилетнюю историю своего развития эта наука приобрела методологически безупречные формы и строгую аксиоматику, так что сегодня ее заслуженно называют классической термодинамикой. Теплопередача, а точнее теория теплообмена и массообмена – это наука, которая изучает процессы распространения тепла (или массы, поскольку выявлена явная аналогия таких процессов) в пространстве. Процессы распространения тепла в пространстве, при всем их многообразии, и являются предметом изучения этой науки. Основные понятия и законы теории теплопереноса также были сформулированы в рамках общефизической теории на заре ее бурного развития. Например, основы аналитической теории теплопроводности были заложены Ж. Фурье еще в 1822 году. В середине XIX века были сформулированы основы теории подобия, а в 1915 году она впервые была применена В. Нуссельтом для исследования процессов теплообмена. Несколько раньше О. Рейнольдс применил ее при изучении гидродинамических процессов, высказав идею об аналогии между отдельными тепловыми и гидродинамическими явлениями. Как самостоятельная наука теплопередача сложилась в начале XX века, и особенно бурно она стала развиваться в послевоенные годы. Здесь решающий вклад был внесен нашими соотечественниками, среди которых выделяются работы академиков В. М. Кирпичева, М. А. Михеева, С. С. Кутателадзе, Г. Н. Кружилина и др. Для того чтобы разобрать протекающие процессы теплопередачи при рафинировании электролитического хрома, необходимо ознакомиться с используемым оборудованием и технологией производства данного материала. Как мы ознакомились ранее электролитический хром отличается от рафинированного электролитического хрома гораздо меньшим содержанием в последнем кислорода и серы. Ниже приведена сравнительная таблица 3 по химическому составу, двух марок электролитического хрома (далее ЭХ) и рафинированного электролитического хрома (далее ЭРХ-1). Таблица 4
Для получения такого низкого содержания по газовым примесям, таких как кислород и сера, необходим процесс рафинирования хрома. Данный процесс выполняется на печах сопротивления, по типу ОКБ-766А в водородной или вакуумной среде. В представленной работе мы рассмотрим процесс рафинирования, протекающий в водородной среде. Печь ОКБ-766А изображена на рисунке 4 и представляет собой печь сопротивления состоящую из: Верхняя металлическая крышка; Верхний экран; Металлический корпус печи; Нагреватели; Вертикальный экран; Термопара; Ввод водорода в печь; Нижнее дно; Установочная станина; Холодильник; Свеча. Тигель;  Рисунок 4. Печь ОКБ-766А. В данном случае водород выступает в роли инертной среды. При попадании в печь таких газов, как кислород или азот, произойдет окисление материала и приведет к бессмысленности проведения процесса. В самом начале режима весь кислород удаляется из печи вакуумированием. Далее внутрь запускается водород и начинается процесс нагрева. На рисунке 5 представлен температурный график. 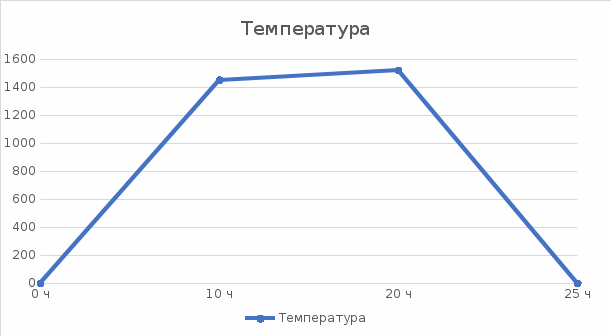 Рисунок 5. Температурный график. Процесс выгорания кислорода и серы начинается на отметке 1450 °С и продолжается до отметки 1520 °С. Далее напряжение на нагреватели отключается и идет процесс остывания. Теперь необходимо разобрать представленный технологический процесс с точки зрения протекающих в нем процессов теплопередачи и основных понятий. Исследования показывают, что теплопередача является сложным процессом. При изучении этот процесс расчленяют на простые явления. Различают три элементарных способа переноса теплоты: теплопроводность, конвекцию и тепловое излучение. Теплопроводностью называют перенос теплоты (или внутренней энергии) при непосредственном соприкосновении тел (или частей одного тела) с различной температурой. Явление конвекции наблюдается в движущихся жидкостях или газах. Перенос теплоты при этом происходит просто за счет перемещения вещества в пространстве. Тепловым излучением называется явление переноса теплоты в виде электромагнитных волн с двойным взаимным превращением – тепловой энергии в лучистую и обратно.2 В нашем случае элементарные виде теплообмена не обособлены и в чистом виде встречаются крайне редко. В большинстве случаев один вид теплообмена сопровождается другим. Например, обмен теплотой между твердой поверхностью и жидкостью (или газом) происходит путем теплопроводности и конвекции одновременно и называется конвективным теплообменом или теплоотдачей. В представленной работе задействованы все три вида теплообмена. Основной закон теплопроводности гласит – если в твердом теле, неподвижной жидкости или газе температура в различных точках неодинакова, то, как показывает опыт, теплота самопроизвольно переносится от участков тела с более высокой температурой к участкам с более низкой температурой. Такой процесс называется теплопроводностью. Внутренний механизм явления теплопроводности объясняется на основе молекулярно-кинетических представлений; перенос энергии при этом осуществляется вследствие теплового движения и энергетического взаимодействия между микрочастицами (молекулами, атомами, электронами), из которых состоит данное тело. Процесс теплопроводности неразрывно связан с распределением температуры внутри тела. Поэтому при его изучении прежде всего необходимо установить понятия температурного поля и градиента температуры. Температурное поле. Температура, как известно, характеризует тепловое состояние тела и определяет степень его нагретости. Так как тепловое состояние отдельных частей тела в процессе теплопроводности различно, то в общем случае температура t является функцией координат x, y, zи времени τ, т.е. t = ƒ (x, y, z, τ). (а) Совокупность значений температуры для всех точек пространства в данный момент времени называется температурным полем. Уравнение (а) является математическим выражением такого поля. При этом, если температура меняется во времени, поле называется неустановившимся (нестационарным), а если не меняется – установившимся (стационарным). Температура может быть функцией одной, двух и трех координат. Соответственно этому и температурное поле называется одно-, двух- и трехмерным. Наиболее простоит вид имеет уравнение одномерного стационарного температурного поля: t = t(x). (б) Градиент температур. При любом температурном поле в теле всегда имеются точки с одинаковой температурой. Геометрическое место таких точек образует изотермическую поверхность. Так как в одной и той же точке пространства одновременно не может быть двух различных температур, то изотермические поверхности друг с другом не пересекаются; все они или замыкаются на себя, или кончаются на границах тела. Следовательно, изменение температуры в теле наблюдается лишь в направлениях, пересекающих изотермические поверхности (например, направление x, рисунок 6). При этом наиболее резкое изменение температуры получается в направлении нормали nк изотермической поверхности. Предел отношения изменения температуры ∆tк расстоянию между изотермами по нормали ∆nназывается градиентом температур и обозначается одним из следующих символо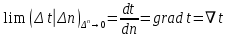в:  . (в)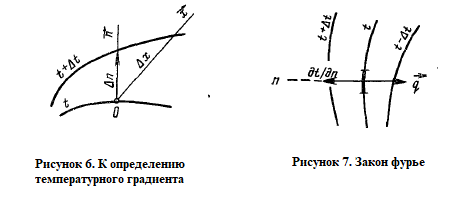 Температурный градиент является вектором, направленным по нормали к изотермической поверхности в сторону возрастания температуры °С/м. Тепловой поток. Теплота самопроизвольно переносится в сторону убывания температуры. Количество теплоты, переносимое через какую-либо изотермическую поверхность в единицу времени, называется тепловым потоком Q. Тепловой поток, отнесенный к единице площади изотермической поверхности, называется плотностью теплового потока q. Плотность теплового потока есть вектор, направление которого совпадает с направлением распространения теплоты в данной точке и противоположно направлению вектора температурного градиента (рисунок 7). Закон Фурье. Изучая процесс теплопроводности в твердых телах, Фурье экспериментально установил, что количество переданной теплоты пропорционально падению температуры, времени и площади сечения, перпендикулярного направлению распространения теплоты. Если количество переданной теплоты отнести к единице площади сечения и единице времени, то установленную зависимость можно записать: 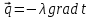 . (г)Уравнение (г) является математическим выражением основного закона теплопроводности – закона Фурье. Этот закон лежит в основе всех теоретических и экспериментальных исследований процессов теплопроводности.3 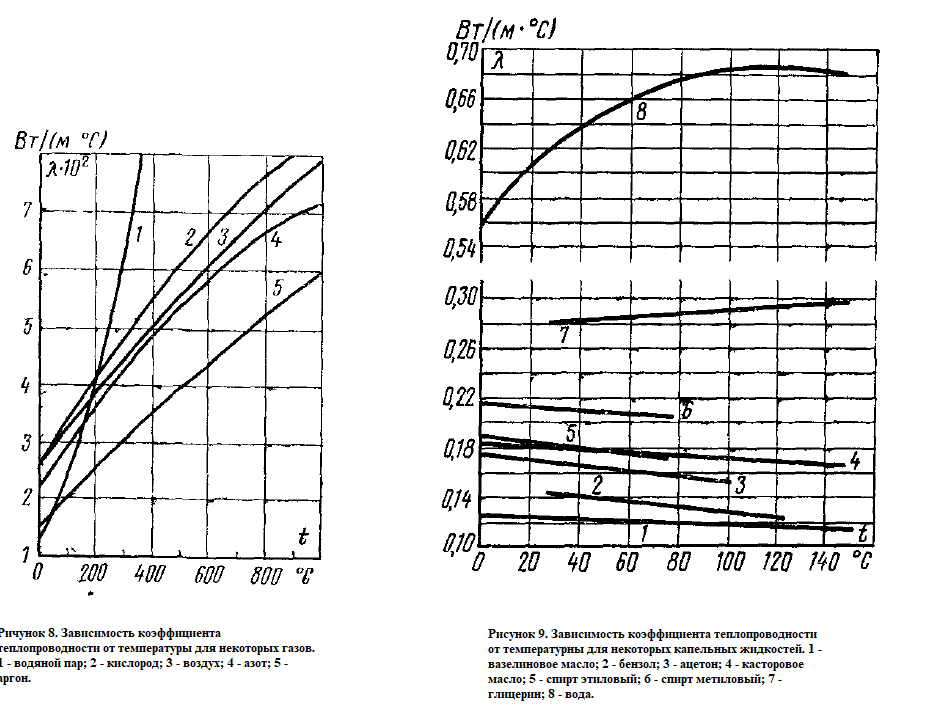 Коэффициент теплопроводности. Коэффициент пропорциональности  в уравнении (г) называется коэффициентом теплопроводности. Он является физическим свойством вещества и характеризует его способности проводить теплоту: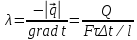 (д)Значение коэффициента теплопроводности представляет собой количество теплоты, которое проходит в единицу времени через единицу площади изотермической поверхности при температурном градиенте, равном единице. Для различных веществ коэффициент теплопроводности различен и в общем случае зависит от структуры, плотности, влажности, давления и температуры. Все вместе взятое затрудняет выбор правильного значения коэффициента теплопроводности. Поэтому при ответственных расчетах значение коэффициента теплопроводности следует определять путем специального изучения применяемого материала. В технических же расчетах значения коэффициента теплопроводности обычно берутся по справочным таблицам. При этом надо следить лишь за тем, чтобы физические характеристики материала (структура, плотность, влажность, температура, давление) были соответственны. Так как при распространении теплоты температура в различных частях тела различна, то в первую очередь важно знать зависимость коэффициента теплопроводности от температуры. Для большого числа материалов эта зависимость оказывается почти линейной, т.е. 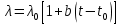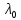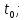можно принять: (е)где  – коэффициент теплопроводности при температуре  b – постоянная, определяемая опытным путем.а) Коэффициент теплопроводности газов лежит в пределах 0,005 – 0,5 Вт/(м·°С). С повышением температуры коэффициент теплопроводности возрастает, от давления практически не зависит. Закон аддитивности для коэффициента теплопроводности неприменим; поэтому для смеси газов коэффициент теплопроводности при отсутствии табличных данных достоверно может быть определен только опытным путем.б) Коэффициент теплопроводности капельных жидкостей лежит в пределах 0,08 – 0,7 Вт/(м·°С). С повышением температуры для большинства жидкостей он убывает, исключение составляет лишь вода и глицерин. в) Коэффициент теплопроводности строительных и теплоизоляционных материалов лежит в пределах 0,02 – 3,0 Вт/(м·°С). С повышением температуры он возрастает. Как правильно, для материалов с большой плотность коэффициент теплопроводности имеет более высокие значения. Он зависит также от структуры материала, его пористости и влажности. Для влажного материала коэффициент теплопроводности может быть значительно выше, чем для сухого и воды в отдельности. г) Коэффициент теплопроводности металлов лежит в пределах 20 – 400 Вт/(м·°С). Самым теплопроводным металлом является серебро ( = 410), затем идут чистая медь ( = 395), золото ( = 300), алюминий ( = 210) и т.д. (рисунок 10). 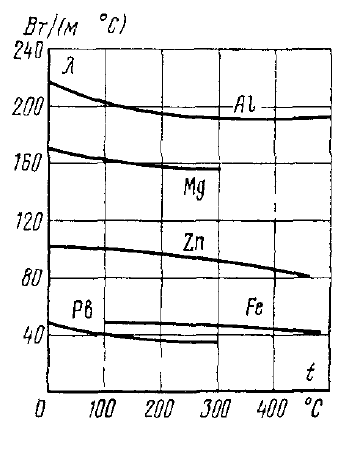 Рисунок 10. Зависимость коэффициента теплопроводности от температуры для некоторых металлов. Для большинства металлов с повышением температуры коэффициент теплопроводности убывает. Он также убывает при наличии разного рода примесей. Так, например, для чистой меди = 395, для той же меди, но со следами мышьяка = 142. Для железа с 0,1% углерода = 52, с 1,0% углерода = 40 и с 1,5% углерода = 36. Для закаленной углеродистой стали коэффициент теплопроводности на 10-15% ниже, чем для мягкой. Однако установить какую-либо общую закономерность влияния примесей пока невозможно. Поэтому для металлов и их сплавов непосредственный опыт является единственным способом определения достоверного значения коэффициента теплопроводности. Так как теплопроводность металлов, так же, как и их электропроводность, в основном определяется переносом свободных электронов, то для чистых металлов эти значения пропорциональны друг другу (закон Видемана – Франца). Ниже на основе закона Фурье приведены расчетные формулы теплопроводности для разных тел при стационарном режиме. Строго эти формулы справедливы лишь для твердых тел. В применении их к жидкостям и газам необходимо учитывать возможное влияние конвекции и теплового излучения. 4 |