Реферат на тему: Процессы теплопередачи при рафинировании хрома. теплопередача. Процессы теплопередачи при рафинировании хрома
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
Теплопроводность плоской стенкиОднородная стенка. Рассмотрим однородную стенку толщиной 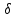 (рисунок 11), коэффициент теплопроводность (рисунок 11), коэффициент теплопроводность  которой постоянен. На наружных поверхностях стенки поддерживаются постоянные температуры t1 и t2. Температура изменяется только в направлении оси x. В этом случае температурное поле одномерно, изотермические поверхности плоские и располагаются перпендикулярно оси x. которой постоянен. На наружных поверхностях стенки поддерживаются постоянные температуры t1 и t2. Температура изменяется только в направлении оси x. В этом случае температурное поле одномерно, изотермические поверхности плоские и располагаются перпендикулярно оси x.На расстоянии xвыделим внутри стенки слой толщиной dx, ограниченный двумя изотермическими поверхностями. На основании закона Фурье для этого случая можно написать: 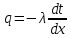 или или 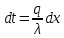 (а) (а)Плотность теплового потока qпри стационарном тепловом режиме постоянна в каждом сечении, поэтому: 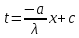 (б) (б)Постоянная интегрирования Cопределяется из граничных условий, а именно при x= 0, t = t1 = C, а при x = 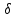 t = t2. Подставляя эти значения в уравнение (б), имеем: t = t2. Подставляя эти значения в уравнение (б), имеем: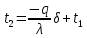 (в) (в)Из уравнения (в) определяется неизвестное значение плотности теплового потока q, а именно: 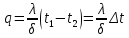 (1-2) (1-2)Следовательно, количество теплоты, переданное через единицу поверхности стенки в единицу времени, прямо пропорционально коэффициенту теплопроводности  и разности температур наружных поверхностей ∆tи обратно пропорционально толщине стенки и разности температур наружных поверхностей ∆tи обратно пропорционально толщине стенки 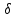 . . Уравнение (1-2) является расчетной формулой теплопроводности плоской стенки. Оно связывает между собой четыре величины%: q,  , , 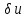 ∆t. Зная из них любые три, можно найти четвертую: ∆t. Зная из них любые три, можно найти четвертую: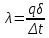 , , 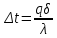 и и 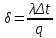 . (г) . (г)Отношение  / /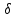 называется тепловой проводимостью стенки, а обратная величина называется тепловой проводимостью стенки, а обратная величина 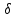 / / – термическим сопротивлением. Последнее определяет падение температуры в стенке на единицу плотности теплового потока. – термическим сопротивлением. Последнее определяет падение температуры в стенке на единицу плотности теплового потока.Если в уравнение (б) подставить найденные значения С и плотности теплового потока q, то получим уравнение температурной кривой: 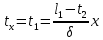 (1-3) (1-3)Последнее показывает, что при постоянном значении коэффициента теплопроводности температура однородной стенки изменяется по линейному закону. В действительности же вследствие свой зависимости от температуры коэффициент теплопроводности является переменной величиной. Если это обстоятельство учесть, то получим иные, более сложные расчетные формулы.5 Для подавляющего большинства материалов зависимость коэффициента теплопроводности от температуры имеет линейный характер вида  = =  0 (1 + bt). В этом случае на основании закона Фурье для плоской стенки имеем: 0 (1 + bt). В этом случае на основании закона Фурье для плоской стенки имеем: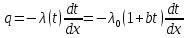 (д) (д)Теплопроводность цилиндрической стенкиОднородная стенка. Рассмотрим однородную цилиндрическую стенку (в нашем случае цилиндрический тигель) длиной l, с внутренним радиусом r1 и внешним r2. Коэффициент теплопроводности материала  постоянен. Внутренняя и внешняя поверхность поддерживаются при постоянных температурах t1 и t2, причем t1> t2 (рисунок 11) и температура изменяется только в радиальном направлении r. Следовательно, температурное поле здесь будет одномерным, а изотермические поверхности цилиндрическими, имеющими с трубой общую ось. Выделим внутри стенки кольцевой слой радиусом rи толщиной dr, ограниченный изотермическими поверхностями. Согласно закону Фурье, количество теплоты, проходящее в единицу времени через этот слой, равно: постоянен. Внутренняя и внешняя поверхность поддерживаются при постоянных температурах t1 и t2, причем t1> t2 (рисунок 11) и температура изменяется только в радиальном направлении r. Следовательно, температурное поле здесь будет одномерным, а изотермические поверхности цилиндрическими, имеющими с трубой общую ось. Выделим внутри стенки кольцевой слой радиусом rи толщиной dr, ограниченный изотермическими поверхностями. Согласно закону Фурье, количество теплоты, проходящее в единицу времени через этот слой, равно: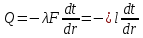 (а) (а)Разделив переменные, имеем: 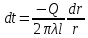 (б) (б)После интегрирования уравнения (б) находим: 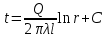 (в) (в)Подставляя значения переменных на границах стенки (при r = r1,t = t1 и при r = r2, t = t2) и исключая постоянную C, получаем следующую расчетную формулу: 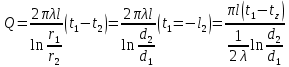 (1-4) (1-4)Следовательно, количество теплоты, переданное в единицу времени через стенку тигля, прямо пропорционально коэффициенту теплопроводности  , длине l и температурному напору ∆t = t1 – t2 и обратно пропорционально натуральному логарифму отношения внешнего диаметра трубы d2 к внутреннему d1. Формула (1-4) справедлива и для случая, когда t1 , длине l и температурному напору ∆t = t1 – t2 и обратно пропорционально натуральному логарифму отношения внешнего диаметра трубы d2 к внутреннему d1. Формула (1-4) справедлива и для случая, когда t1 Количество теплоты, проходящее через стенку трубы может быть отнесено либо к единице длины l, либо к единице внутренней F1 или внешней F2 поверхности тигля. Так как площади внутренне и внешней поверхностей трубы различны, то различными получаются и значения плотностей тепловых потоков q1 и q2. Взаимная связи между ними определяется соотношением: 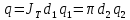 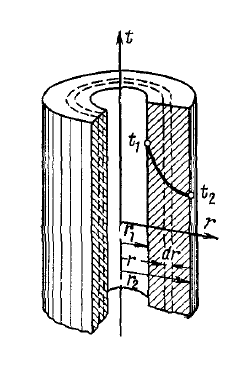 Рисунок 11. Однородная цилиндрическая стенка. |
