Проектирование стеклопластиковой панел укрытия антенного комплекса
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
   УДК 521, 624.041 УДК 521, 624.041ПРОЕКТИРОВАНИЕ СТЕКЛОПЛАСТИКОВОЙ ПАНЕЛ УКРЫТИЯ АНТЕННОГО КОМПЛЕКСА Шмеер Владислав Александрович магистрант, ФСТ, АлтГТУ Россия, город Барнаул Маркин Виктор Борисович д.т.н., профессор АлтГТУ, ФСТ, АлтГТУ, Россия, город Барнаул Аннотация Еще недавно для проектирования материалов и конструкций использовались расчеты классической механики, но в современных, резко меняющихся условиях для ускорения и автоматизации проектирования используют программные пакеты САПР (SolidWorks, Autodesk, Inventor, Ansys и др.). В работе сделан анализ основного значения, определяющего работоспособность конструкции стеклопластиковой панели укрытия антенного комплекса – максимального прогиба при действии сосредоточенного усилия, соответствующего прилагаемому воздействию. Проведено сравнение результатов физико-механического исследования стеклопластика и расчетных значений прогибов и напряжений, полученных по уравнениям классической строительной механики композитных конструкций и программного продукта SolidWorks. Ключевые слова: стеклопластик, панель укрытия, программа SolidWorks, решение Навье, метод Бубнова-Галеркина строительная механика, радиопрозрачность, Современные антенные комплексы нуждаются в изоляции антенного оборудования и излучателей от внешней среды, способной влиять на мощность и поляризацию электромагнитного излучения высокой частоты. В этом направлении хорошо зарекомендовали себя композиционные материалы на основе стеклянных волокон и полимерных связующих эпоксидной группы, способных кроме основных свойств радиопрозрачности, обладать характеристиками, позволяющими работать в жестких условиях механических и климатических воздействий (рисунок 1). а   б Рисунок 1. Антенные комплексы, имеющие защитные укрытия: а – «Седьмое чудо света» - высокоинтеллектуальная многофункциональная РЛС; б – передвижной радиолокационный комплекс В современных условиях для защитных укрытий таких комплексов должны использоваться материалы, физико-механические характеристики которых позволяют сохранять целостность антенных устройств от ветровых и иных нагрузок. Цель проведенных исследований состояла в экспериментальном определении параметров напряженно-деформированного состояния стеклопластиковой панели и установлении корреляции полученных значений с данными, получаемыми расчетным путем. В качестве расчетных методов использовался программный продукт SolidWorks, а также теория изгиба упругой тонкой пластины, из которой были выделены два метода: решение Навье и вариационный метод Бубнова-Галёркина. Программа SolidWorks использует метод конечных элементов (МКЭ), который представляет собой эффективный численный метод решения инженерных и физических задач [3]. Область его применения соответствует анализу напряжений в конструкциях различного класса и назначения. Он является численным методом решения дифференциальных уравнений, встречающихся в расчетных схемах конструкций современной техники, и имеет ряд преимуществ перед многими другими численными методами. Главные достоинства МКЭ:
Определение физико-механических характеристик образцов стеклопластика (препрег: стеклоткань – связующее ЭХД-М) проводилось на исследовательском комплексе INSTRON- по методу трехточечного изгиба. При реальных испытаниях не используются упрощения расчетов, что позволяет объективно определить характеристики материала [2]. На рисунке 2 представлены кривые нагружения образцов, т.е. связь между прикладываемой нагрузкой и удлинением образцов до разрушения. 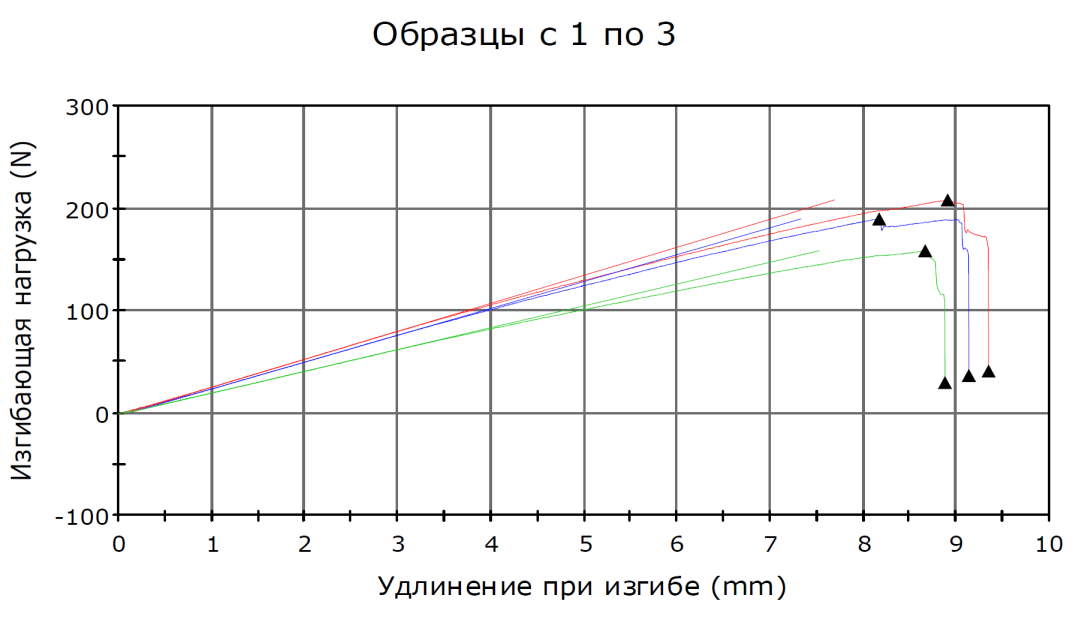 Рисунок 2 – Кривые нагружения, полученные для выборки из трёх образцов стеклопластика, с соответствующими касательными для определения модуля упругости при изгибе В таблице 1 представлены полученные при проведении экспериментов данные, позволяющие оценить физико-механические характеристики стеклопластика и провести соответствующий статистический анализ. Таблица 1. Результаты проведенных испытаний образцов стеклопластика на изгибные нагрузки
Следовательно, средние значения полученных характеристик: максимальное напряжение при изгибе 335,3 МПа, при прогибе 9,11 мм и модуле упругости 14,14 ГПа. Эти значения были использованы при классическом и программном расчете напряженно-деформированного состояния и прогиба пластины. В методе конечных элементов и теоретических расчетов пластин, чтобы упростить задачу и свести её к двумерной, с самого начала вводятся некоторые гипотезы, называемые гипотезами Кирхгофа. Они заключаются в следующем: 1. Точки пластины, расположенные до ее изгиба на прямой, нормальной к срединной плоскости, при изгибе остаются на этой прямой. Эта прямая поворачивается, оставаясь нормальной к изогнутой срединной плоскости. Данная гипотеза аналогична гипотезе плоских сечений в теории изгиба балок, и ее часто называют гипотезой прямых нормалей. 2. На основе гипотезы прямых нормалей установлен линейный закон изменения по толщине нормальных напряжений изгиба и касательных напряжений кручения и получены формулы для углов поворота и прогибов. 3. Слои пластины, параллельные срединной плоскости, не давят друг на друга. Из этой гипотезы следует, что в любом сечении пластины, параллельном срединной плоскости, нормальные напряжения равны нулю и каждый элемент слоя пластины, параллельного срединной плоскости, в общем случае изгиба находится в плоском напряженном состоянии. 4. Кроме того, принимается, что материал пластины однороден, макро-изотропен, а возникающие напряжения ниже предела пропорциональности, и поэтому напряжения и деформации связаны между собой законом Гука. 5. Интенсивности изгибающих моментов вдоль оси X и Y в пластине принято обозначать через Mx и My, а интенсивность крутящих моментов Mxy. Для определения сходимости результатов в программе SolidWorks была смоделирована пластина тех же размерах и физических характеристик материала, что и при испытании на изгиб. Структура расчета состоит из следующих этапов: моделирование испытания на изгиб, расчет деформации при изгибе, напряжения в пластине и запаса прочности при нагружении в пределах потери прочности. Результаты расчета приведены на рисунке 3.  а б    в  г Рисунок 3. Схема закрепления и нагружения образцов (а); результирующее перемещение в пластине при нагружении (б); распределение напряжений в пластине (в); распределение запаса прочности вдоль пластины (г) Расчеты, проведенные в программе SolidWorks, относятся к действию на пластину сосредоточенного усилия в её геометрическом центре при условии шарнирного опирания краёв пластины. Сосредоточенное усилие обеспечило максимальный прогиб в центре пластины порядка 6 мм, максимальное напряжение около 190 МПа и запас прочности 1,8. Проведен расчет основной характеристики упругой тонкой композитной пластины по методам Навье и Бубнова-Галеркина. Решение Навье рассматривает тонкую пластину, шарнирно опертую по всем краям и нагруженную поперечной сосредоточенной нагрузкой Р в точках пластины с координатами х0, у0. Максимальный прогиб рассчитывается из функции прогиба, определяемой строительной механикой композитных конструкций [1]: 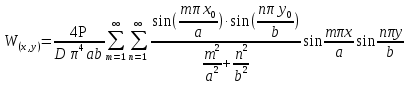 (1) (1)где: 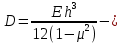 цилиндрическая жесткость пластины; цилиндрическая жесткость пластины;а и b – размеры пластины в плоскости, мм; h – толщина пластины, мм; μ – коэффициент Пуассона; (m= 1, 3, 5 …, n= 1, 3, 5 …). Для 7 членов ряда максимальный прогиб при a = b равен 4,7 мм. Метод Бубнова-Галеркина основан на свойстве ортогональных функций и позволяет определять максимальный прогиб пластины в её центре в соответствии с соотношением: 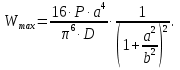 Для квадратной пластины (a=b) при тех же значениях толщины пластины, модуля упругости и коэффициента Пуассона максимальный прогиб равный 6,88 мм. По результатам проведенных экспериментов и расчетов можно провести корреляцию значений максимального прогиба (рисунок 4) и сделать соответствующие выводы. Максимальный прогиб пластины, мм 0 1 2 3 4 5 6 7 8 9  1 2 3 4 Рисунок 4. Максимальный прогиб пластины для различных методов определения: 1 – из эксперимента; 2 – из расчетной программы SolidWorks; 3 – по методу Навье; 4 – по методу Бубнова-Галеркина 1. Максимальное удлинение пластины показало испытание на изгиб, что связано в большей степени с масштабным фактором, поскольку размеры образцов для испытаний и способ их закрепления отличаются от реальных параметров при расчетах; 2. Относительная разница между значениями, полученными при испытании на изгиб, и расчетами в программе SolidWorks, составляет около 20 %. Это позволяет считать, что данный метод позволяет проводить конструкционный расчет с допустимой точностью; 3. Метод Бубнова-Галеркина, являясь вариационным, показывает значение максимального прогиба, аналогичного расчетному из программы SolidWorks. Из этого следует, что метод конечных элементов, использованный в программе, базируется на классических положениях строительной механики. 3. Решение Навье носит оценочный характер, и позволяет провести расчет прогиба с заданной точностью, зависящий от количества членов ряда. С увеличением m и n приближенное значение максимального прогиба будет возрастать и приближаться к решению, получаемому в методе Бубнова-Галеркина. Таким образом, в работе сделан анализ основного значения, определяющего работоспособность конструкции стеклопластиковой панели укрытия антенного комплекса – максимального прогиба при действии сосредоточенного усилия, соответствующего прилагаемому воздействию. Список литературы:
|
