Основы гидравлики. Профессия Основы гидравлики Модуль г. Новокуйбышевск

• Название: Профессия Основы гидравлики Модуль г. Новокуйбышевск
• Анкор: Основы гидравлики
• Дата: 19.03.2022
• Размер: 2.67 Mb.
• Имя файла: Основы гидравлики.doc
• Тип: Документы; #404443
• страница: 3 из 5

3.3. Основы гидростатики

3.3.1. Гидростатическое давление и его свойства

Гидростатика – раздел гидравлики, изучающий законы равновесия жидкостей. Для изложения этих законов необходимо вначале рассмотреть силы, действующие на некоторый объём покоящейся жидкости. Внешние силы, действующие на этот объём, могут быть разделены на две группы:

• 
  массовые (или объёмные) силы, которые пропорциональны массе выделенного объёма жидкости (или при постоянной плотности среды пропорциональны объёму) и действуют на все частицы среды этого объёма. Примером массовых сил являются силы тяжести, центробежная сила и др;
  

• 
  поверхностные силы, которые действуют на внешней поверхности выделенного объёма жидкости и пропорциональны площади этой поверхности. Примером поверхностных сил являются силы давления поршня на жидкость, давления стенок сосуда на жидкость, атмосферного давления на свободную поверхность жидкости и т.п. Поверхностные силы распределены по поверхности выделенного объёма жидкости непрерывно.
  

Под действием внешних сил в каждой точке рассматриваемого объёма покоящейся жидкости возникают внутренние силы, которые обуславливают напряжённое состояние жидкости. Напряжённое состояние в каждой точке жидкости характеризуется давлением.

Рассмотрим какой-либо объём жидкости, находящейся в равновесии (рис 3).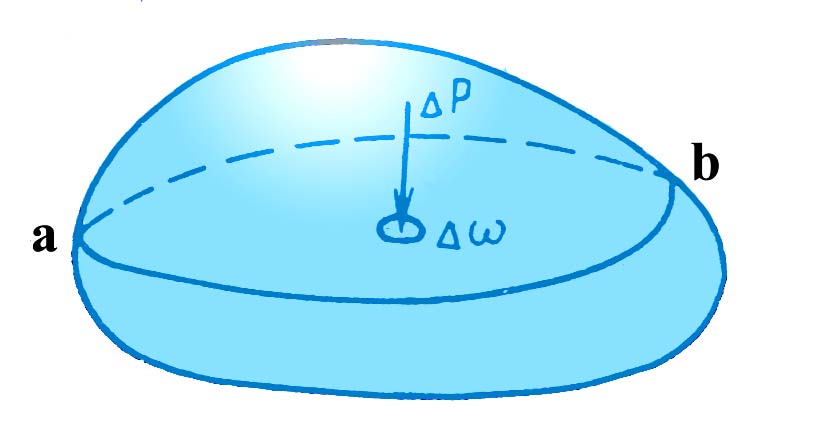


Рис.3.
Если этот объём рассечь некоторой плоскостью ab на две части и мысленно отбросить верхнюю часть, то для сохранения равновесия нижней части необходимо к плоскости ab приложить силы, эквивалентные действию верхней отброшенной части на нижнюю. Пусть на площадку  действует сила Р, представляющая собой равнодействующую всех приложенных к различным точкам этой площадки сил, обусловленных воздействием отброшенной части объёма жидкости на площадку . Тогда отношение Р/ = Р_ср представляет собой среднее гидростатическое давление на площадку , т.е. среднее гидростатическое давление есть отношение поверхностной силы, действующей на некоторую поверхность рассматриваемого объёма жидкости, к площади этой поверхности.

Если плоскость ab расположена горизонтально, параллельно свободной поверхности жидкости, то в любой точке этой плоскости среднее гидростатическое давление одинаково. Но если плоскость расположена наклонно или вертикально, то в разных точках её гидростатическое давление будет различно, находясь в зависимости от глубины погружения их под свободную поверхность жидкости.

В связи с этим кроме среднего гидростатического давления вводится понятие гидростатического давления в данной точке. Разница между истинным давлением в точке и средним давлением в пределах площадке  будет тем меньше, чем меньше эта площадка.

Таким образом, гидростатическим давлением в точке называется предел отношения силы давления к площади, на которую она действует, при стремлении этой площади к нулю, т.е. при стягивании площадки в точку.

Гидростатическое давление можно отсчитывать либо от нуля, либо от атмосферного давления. Если давление Р отсчитывают от нуля, то его называют абсолютным, а если от атмосферного давления – избыточным или манометрическим. Следовательно, абсолютное давление
Р_абс = Р_а + Р_изб (15)
Гидростатическое давление измеряется в единицах силы, делённых на единицу площади, т.е. Р = сила/площадь.

За единицу давления в системе СИ принято равномерно распределённое давление, при котором на площадь 1м² действует сила 1Н, эта единица называется Паскалем (Па).

На практике широко используется внесистемная единица – техническая атмосфера (ат), равная 0,1 МПа.

Гидростатическое давление обладает двумя важными свойствами:

• 
  на поверхности жидкости гидростатическое давление всегда направлено по нормали внутрь рассматриваемого объёма жидкости. При этом под поверхностью жидкости понимают не только поверхности раздела жидкости с газообразной средой или твёрдыми стенками, но и поверхности элементарных объёмов, мысленно выделяемых из общего объёма жидкости;
  

• 
  в любой точке внутри жидкости гидростатическое давление по всем направлениях одинаково, т.е. давление не зависит от угла наклона площадки, на которую оно действует в данной точке.
  

Вопросы к размышлению:

1. 
   Что называют гидростатикой?
   
2. 
   Какое гидростатическое давление называют абсолютным.
   
3. 
   Назовите единицу измерения гидростатического давления.
   
4. 
   Какими свойствами обладает гидростатическое давление?
   

3.3.2.Основное уравнение гидростатики

Покой жидкости может быть абсолютным и относительным. Абсолютным покоем называется покой жидкости относительно Земли. Относительным покоем называется равновесие, при котором нет движения частиц жидкости относительно друг друга и по отношению к стенкам сосуда, в котором она находится, но сосуд вместе с жидкостью находится в движении относительно Земли.

Рассмотрим жидкость, находящуюся в сосуде в абсолютном покое. Пусть на нее действует одна массовая сила – тяжести. Свободная поверхность жидкости в этом случае, как известно, является горизонтальной плоскостью. Пусть давление на свободной поверхности равно Ро (рис.4).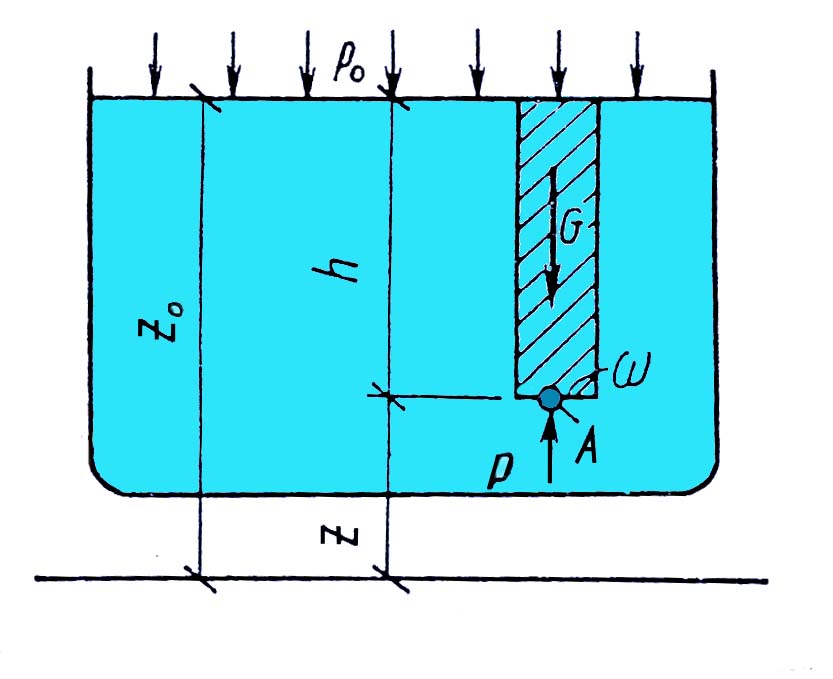



Рис.4.
Найдем гидростатическое давление в точке А, расположенной на глубине h от свободной поверхности. Выделим вокруг точки А горизонтальную площадку  и построим на ней вертикальный цилиндрический объем высотой h.

Так как рассматриваемый объем находится в равновесии, то сумма проекций всех сил на вертикальную ось должна равняться нулю.

На цилиндрический объем действуют следующие силы:

• 
  сверху вниз – сила давления на площадь , равная Ро , и вес жидкости в указанном объеме, равный G = h;
  

• 
  снизу вверх – сила гидростатического давления на нижнюю площадку , равная Р .
  

Следовательно:
Ро  + h - Р  = 0 (16)
Силы давления, действующие на боковую поверхность цилиндра, в уравнение не войдут, так как они горизонтальны и проекции на вертикальную ось не дают.

Сократив на  и перегруппировав члены, получим:
Р = Ро +  h (17)
Это уравнение называют основным уравнением гидростатики. Оно показывает, что абсолютное давление в любой точке покоящейся жидкости на глубине h слагается из давления на свободной поверхности Ро и давления, созданного весом столба жидкости, h.

При открытом сосуде первое слагаемое в правой части уравнения равно атмосферному давлению, второе слагаемое h будет представлять собой избыточное давление. Для точек, расположенных на одинаковой глубине под уровнем свободной поверхности, избыточное гидростатическое давление будет одинаковым. Совокупности точек с одинаковыми h образуют поверхности с одинаковыми давлениями, называемые поверхностями уровня. В данном случае поверхностями уровня являются горизонтальные плоскости, а свободная поверхность является одной из поверхностей уровня.

Поверхности уровня обладают двумя основными свойствами:

• 
  

  Свойства поверхностей уровня

  две поверхности уровня не пересекаются между собой. Действительно, если бы поверхность уровня с давлением Р₁ пересекалась с поверхностью уровня с давлением Р₂, тогда на линии пересечения этих поверхностей давление было бы одинаковым, т.е. Р₁ = Р₂, что невозможно, так как Р₁ не равно Р₂. Следовательно, поверхности уровня не могут пересекаться между собой;
  
• 
  равнодействующая массовых сил направлена нормально к поверхности уровня. Так как в рассматриваемом случае на жидкость действует только сила тяжести, направленная по вертикали, то поверхность уровня будет горизонтальной.
  

Вопросы к размышлению:

1. 
   Что называется относительным покоем?
   
2. 
   Что показывает основное уравнение гидростатики?
   
3. 
   Какими свойствами обладают поверхности уровня?
   

3.3.3.Закон Паскаля

Основное уравнение гидростатики Р = Ро + h показывает, что давление на поверхности жидкости Ро передается в любую точку внутри жидкости без изменения. Действительно, для точки А, расположенной на глубине h1 под свободной поверхностью жидкости, гидростатическое давление Ра = Ро + h1, а для точки В, расположенной на глубине h2, Рб = Ро + h2 (рис. 5). Как видим, давление Ро одинаково для всех этих двух точек. Точно также давление Ро является одинаковым для всех точек объема жидкости. В связи с этим, учитывая второе свойство гидростатического давления, можно сформулировать закон Паскаля: давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково.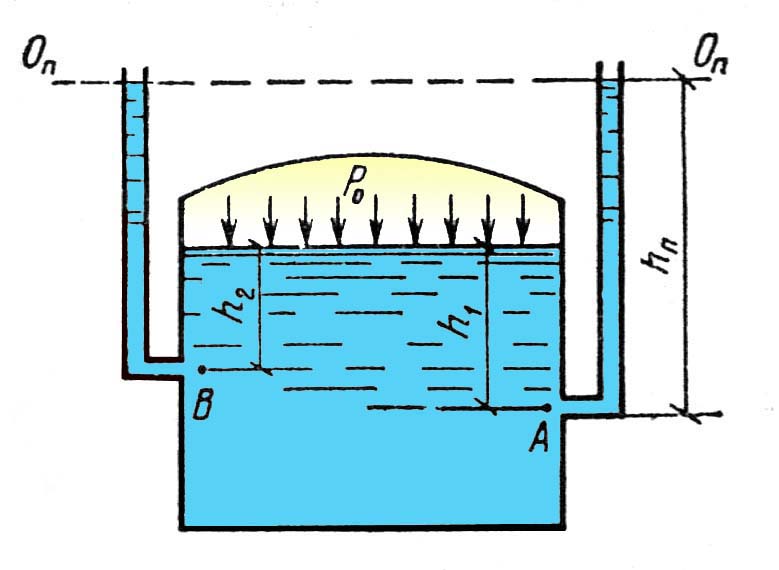

Рис.5.
На использовании закона Паскаля основано устройство простейших гидравлических машин: гидравлических прессов, мультипликаторов (повысителей давления), домкратов, подъемников и др.

На рис.6 показана принципиальная схема гидравлического пресса, который состоит из малого цилиндра с поршнем площадью 1 и большого цилиндра с поршнем площадью 2.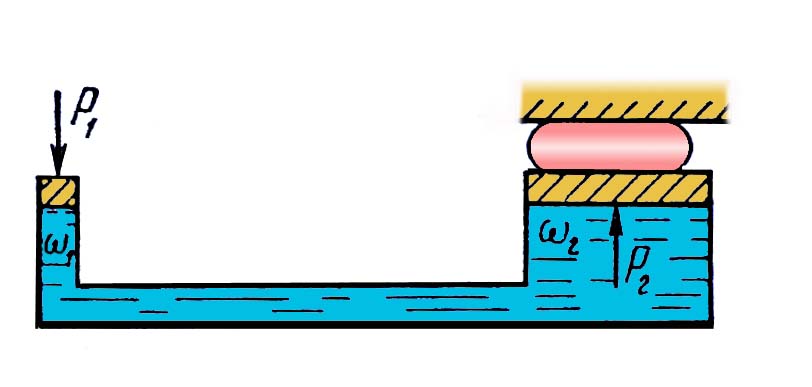


Рис.6.
Цилиндры соединены между собой трубопроводом. Если на поверхность жидкости в малом цилиндре нажать через поршень с силой Р1, то эта сила создаст под поршнем давление Р = Р1/1. По закону Паскаля это давление передается во все точки жидкости. Следовательно, на поршень с площадью 2 передается то же давление Р1 и действует сила давления Р2=Р12. Подставив в это выражение значение Р1, получим:
Р2 = Р1 2/1 (18)
Таким образом, на поршень с площадью 2 через жидкость передается сила Р2, во столько раз большая силы давления Р1, во сколько раз площадь 2 больше площади 1.

Практически развиваемое усилие вследствие трения поршней в цилиндрах будет меньше, чем вычисленное по формуле(18). Это уменьшение учитывается КПД пресса , значение, которого в среднем равно 0,8.

3.3.4.Давление жидкости на плоские стенки

Используя основное уравнение гидростатики, можно найти силу давления жидкости на ограничивающие ее твердые стенки. Эта задача имеет большое практическое значение при расчетах гидротехнических сооружений, резервуаров, устройств.

Полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление в центре тяжести этой площади.

Если давление на свободной поверхности жидкости ро равняется атмосферному, то сила избыточного давления жидкости на плоскую стенку равна
Р_изб = рС_изб ω = γhСω (19)
Таким образом, сила избыточного давления жидкости на плоскую стенку равна весу цилиндрического столба жидкости, основанием которого является площадь стенки ω, а высотой – глубина погружения центра тяжести С площади стенки под свободной поверхностью жидкости hС.

В частном случае, когда стенка расположена горизонтально, например, представляет собой горизонтальное дно сосуда, глубина погружения центра тяжести площади дна равна глубине его расположения под свободной поверхностью, и формула для определения силы избыточного давления на плоское горизонтальное дно сосуда получает вид:

Р_изб = γНω (20)
Из этой формулы видно, что сила давления жидкости на дно сосуда зависит только от площади дна ω и глубины жидкости в сосуде Н и не зависит от формулы сосуда, в который эта жидкость налита.
В опросы к размышлению:
1.Сформулируйте закон Паскаля.

2.На использовании закона Паскаля основано устройство, каких машин?

3. Как определяется сила давления жидкости на плоскую стенку.

3.3.5.Давление жидкости на криволинейные стенки

Закон Архимеда.
В общем случае нахождение силы давления жидкости на поверхности произвольной формы является достаточно сложной задачей. Эта задача решается, как правило, графическим методом путем построения эпюры гидростатического давления.

Однако на практике чаще всего приходится иметь дело с цилиндрическими или сферическими поверхностями, имеющими вертикальную плоскость симметрии, например стенки труб, резервуаров и всевозможных цилиндрических сосудов, шаровые клапаны.

Архимедова сила

Сформулируем закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости в объеме этого тела. Это положение носит название закона Архимеда. Этот закон справедлив и для тел, частично погруженных в жидкость.
Сила Ра называется архимедовой силой, или подъемной силой, а точка ее приложения - центром водоизмещения, который совпадает с центром тяжести вытесненного объема жидкости. Следует иметь в виду, что центр водоизмещения не обязательно совпадает с центром тяжести тела, а может находиться выше или ниже последнего. Совпадение центра тяжести тела и центра водоизмещения наблюдается только в том случае, если погруженное в жидкость тело однородное.

Следовательно, на тело, погруженное в жидкость, действуют две силы: сила тяжести тела G, направленная сверху вниз и приложенная в центре тяжести тела; архимедова сила Ра, направленная снизу вверх и приложенная в центре водоизмещения. В зависимости от соотношения этих сил возможны три случая:

1. 
   G > Ра - тело тонет;
   
2. 
   G < Ра - тело всплывает до тех пор, пока сила тяжести вытесненной жидкости, т.е. Ра, не станет равна силе тяжести вытесненной жидкости, т.е. Ра, не станет равна силе тяжести G;
   
3. 
   G = Ра - тело плавает в погруженном состоянии на любой глубине.
   

Для равновесия плавающего тела помимо равенства сил Ра и G необходимо еще равенство нулю суммарного момента. Для выполнения последнего условия центр тяжести тела и центр водоизмещения должны лежать на одной вертикали.

При воздействии на плавающее тело внешних сил, например ветра, крутого поворота и т.п., оно будет отклоняться от положения равновесия (давать крен). Если центр тяжести С полностью погруженного в жидкость тела расположен ниже центра водоизмещения D (рис.7.), то появляющаяся при крене пара сил стремится возвратить тело в первоначальное положение.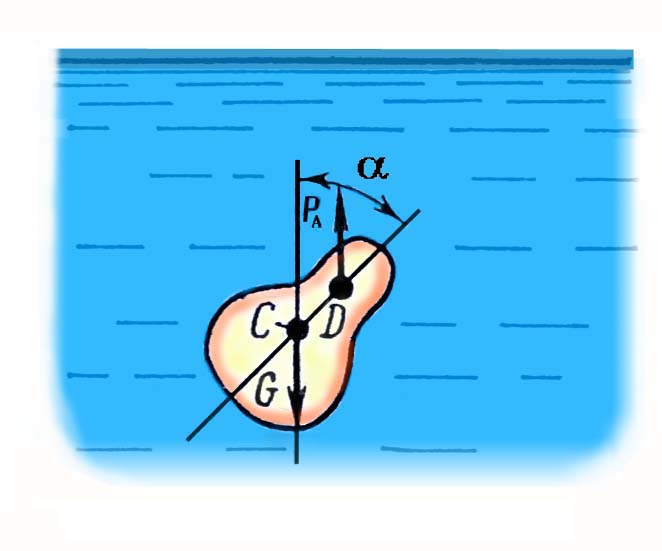


Рис.7.
Такое расположение центров соответствует остойчивому плаванию. Если же центр тяжести С расположен выше центра водоизмещения D (рис.8), плавание будет неостойчивым, так как будучи выведено из состояния равновесия такое тело уже не способно возвратиться в первоначальное положение, а наоборот, под действием появившейся пары сил будет все более от него отклоняться. Наконец, при совпадении центров С и D тело будет находиться в состоянии безразличного равновесия.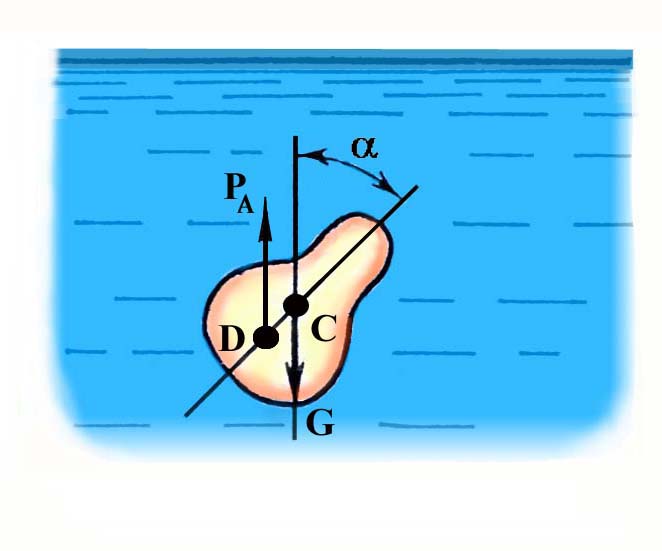


Рис.8.