Основы гидравлики. Профессия Основы гидравлики Модуль г. Новокуйбышевск
 Скачать 2.67 Mb. Скачать 2.67 Mb.
|
3.5. Гидравлическое сопротивление3.5.1.Виды гидравлических сопротивленийРешение многих практических задач гидравлики сводится к нахождению зависимости, определяющей изменения скорости и давления по длине потока. Для этого обычно используются два полученных выше уравнения гидродинамики: Уравнение неразрывности потока: Q = = const (23) и уравнение Бернулли: Z + p/ + 2/2g + h = const (24) Однако эти два уравнения имеют три неизвестных: , р и h, поэтому для их решения необходимо составить третье уравнение, связывающее между собой неизвестные величины. Таким уравнением является зависимость потерь напора h от средней скорости . Как показывают опыты, во многих случаях потери напора примерно пропорциональны квадрату средней скорости движения жидкости, поэтому в гидравлике принято выражать потерянный напор пропорционально скоростному напору, т. е.: h = 2/ 2g (25) где - безразмерный коэффициент пропорциональности, называемый коэффициентом сопротивления. Потери напора потока вызываются сопротивлениями двух видов: Виды сопротивленийсопротивлениями по длине, обусловленными силами трения;местными сопротивлениями, обусловленными изменениями скорости потока по величине и направлению. Потери напора по длине, или, как их еще называют, потери на трение или путевые потери, можно выразить по общей формуле для гидравлических потерь, т. е. hl = тр 2/ 2g (26) где тр - коэффициент сопротивления движению жидкости по длине трубы. Местные потери напора обусловлены местными изменениями формы и размеров живого сечения потока, т. е. деформацией потока при протекании через местные сопротивления. Примерами местных сопротивлений могут служить задвижки, диафрагмы, повороты, вентили и другие устройства, устанавливаемые на трубопроводе (рис. 11). Местные потери напора не зависят от длины потока и поэтому определяются следующим образом: hм = 2/ 2g (27) где - коэффициент местного сопротивления. Эта формула называется формулой Вейсбаха. 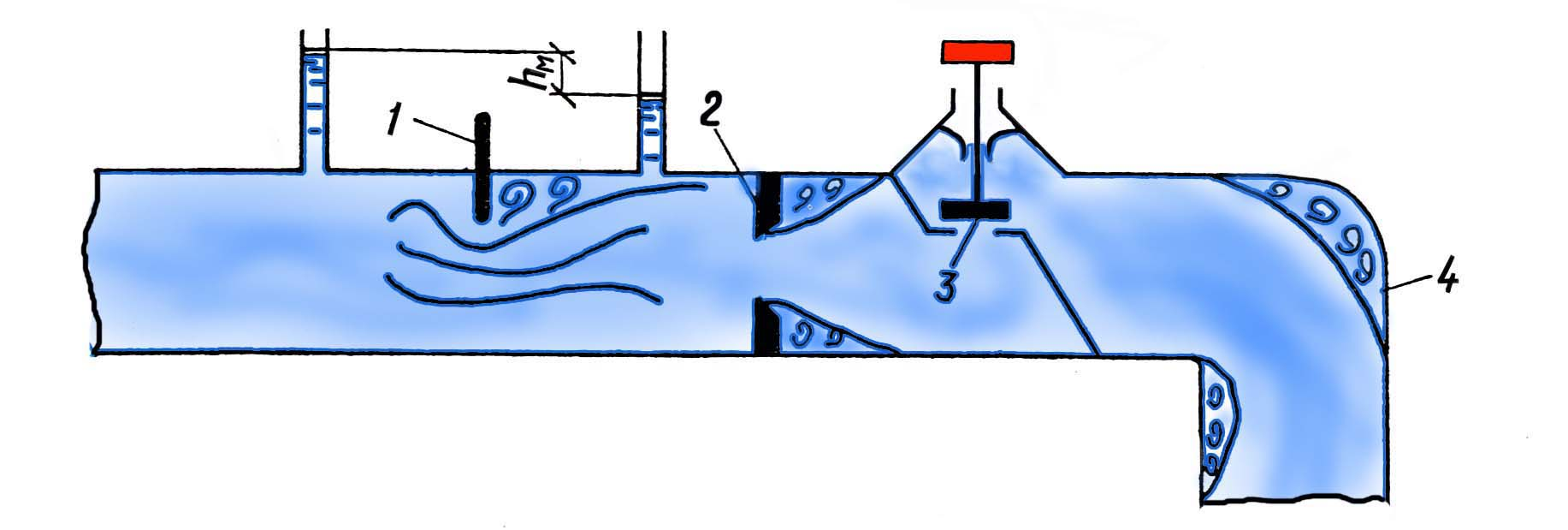 Рис.11. Каждое местное сопротивление характеризуется своим значением коэффициента , определяемым обычно опытным путем. Средняя по сечению скорость движения жидкости в трубопроводе берется либо до местного сопротивления, либо после него, при этом коэффициент данного местного сопротивления будет разным. Чаще всего за расчетную скорость принимают большую из скоростей, т. е. ту, которая соответствует меньшему диаметру трубопровода. Общие потери напора равны сумме потерь напора по длине и местных: Общие потери напораh = hl + hм (28)Если на данном трубопроводе установлено несколько местных сопротивлений, то общие потери напора запишутся в виде: h = hl + hм (29) Нахождение коэффициента и является одной из основных задач гидравлики. Многочисленные экспериментальные исследования показали, что эти коэффициенты зависят от многих факторов, и в частности, от режима движения жидкости. 3.5.2. Режимы движения жидкостиОпыты показывают, что возможны два режима или два вида движения жидкостей и газов: ламинарный и турбулентный. Ламинарное давлениеЛаминарное (параллельноструйное) движение характеризуется упорядоченным перемещением отдельных частиц без перемешивания и без пульсаций скоростей и давлений. Если в прямой трубе постоянного сечения протекает жидкость при ламинарном режиме движения, то все линии тока направлены параллельно оси трубы, т. е. прямолинейны, а поперечные перемещения жидкости в процессе ее течения отсутствуют. Пьезометр, присоединенный к трубе с установившимся ламинарным движением, показывает неизменность давления (и скорости) во времени, отсутствие колебаний (пульсаций).Турбулентное движениеТурбулентное (беспорядочное) движение характеризуется интенсивным перемешиванием частиц жидкости и пульсациями скоростей и давлений. Траектории отдельных частиц жидкости при турбулентном движении имеют вид замысловатых кривых, что говорит о том, что при турбулентном движении наряду с основным продольным перемещением жидкости вдоль трубы существуют поперечные перемещения и вращательное движение отдельных объемов жидкости.Предположение о существовании двух режимов движения жидкости было подтверждено экспериментально английским ученым О.Рейнольдсом. Установка Рейнольдса для исследования режимов движения жидкости показана на рис. 12. 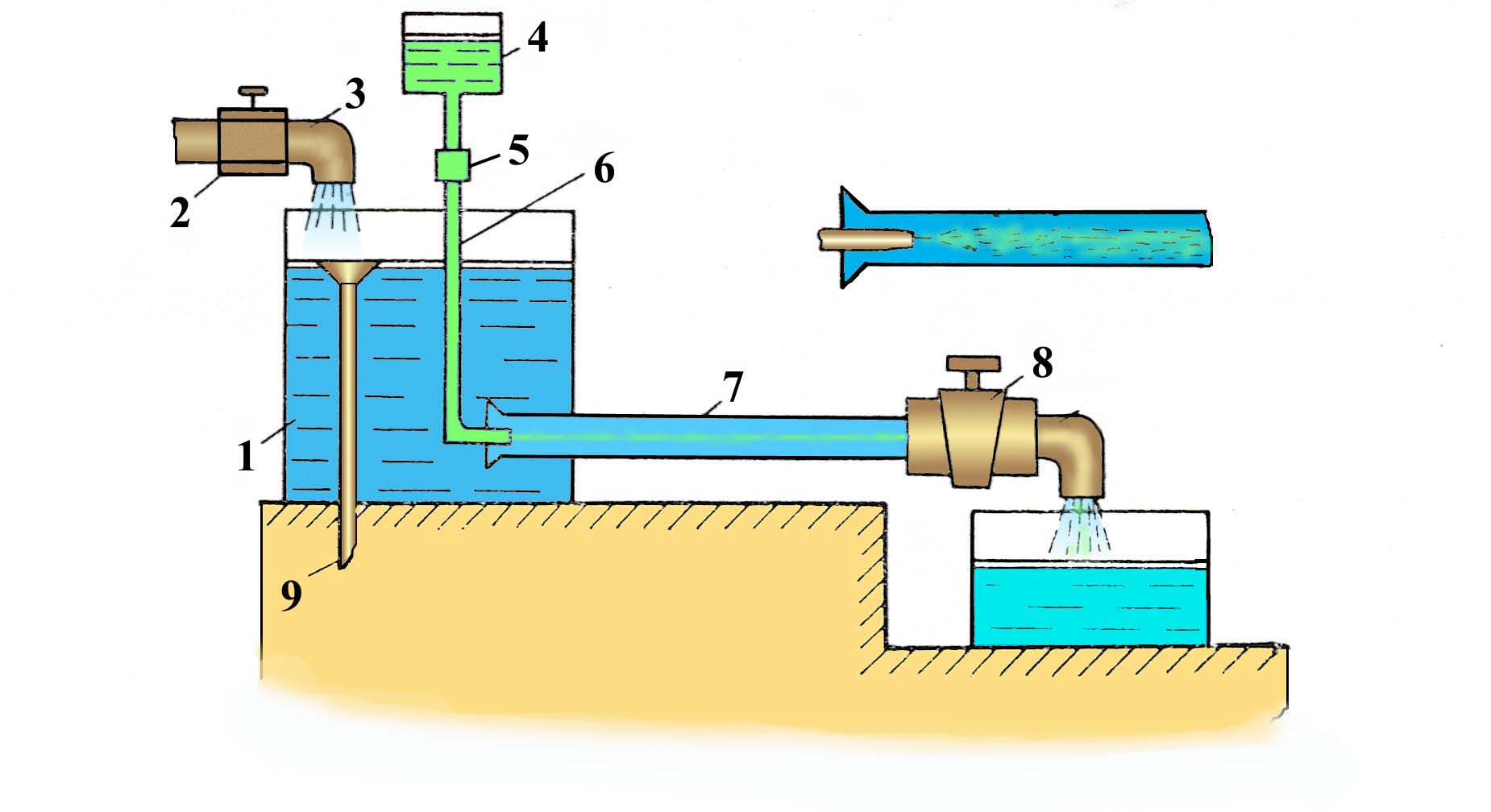 Рис.12. К напорному резервуару 1 в нижней его части присоединена стеклянная трубка 7 с краном 8, которым регулируется скорость потока в трубке. По тонкой трубке 6 к входу в стеклянную трубку 7 подводится окрашенная жидкость из сосуда 4. Для пополнения резервуара 1 и поддержания постоянного уровня жидкости служат трубка 3 с запорным устройством 2 и сливная трубка 9. При малом открытии крана 8 поток в стеклянной трубке 7 будет двигаться с малой скоростью. Если при этом с помощью вентиля 5 пустить в поток подкрашенную жидкость, то можно видеть, что подкрашенная струйка будет двигаться в стеклянной трубке как бы обособленно, не смешиваясь с основным потоком. Струйка краски будет отчетливо видимой вдоль всей стеклянной трубки, что указывает на слоистый характер движения жидкости и на отсутствие перемешивания. Это – ламинарное движение. При постепенном увеличении открытия крана 8 увеличивается скорость движения жидкости, и режим движения переходит в турбулентный. При этом струйка краски приобретает волнообразный характер, а при еще большей скорости совсем размывается и смешивается с жидкостью в трубке 7. При постепенном закрытии крана 8 эти явления протекают в обратном порядке, т. е. турбулентный режим сменяется ламинарным. Смена режимов движения конкретной жидкости в данной трубе происходит при определенной скорости потока, которую называют критической скоростью кр. На основании своих опытов Рейнольдс установил, что значение критической скорости прямо пропорционально кинематической вязкости жидкости и обратно пропорционально диаметру трубы d, т. е.: кр = k/d (30) Причем безразмерный коэффициент пропорциональности k имеет универсальное значение, т. е. одинаков для всех жидкостей и газов, а также для любых диаметров труб. Это безразмерное число называется критическим числом Рейнольдса и обозначается Reкр = крd/ (31) Критическое число РейнольдсаЗначение критического числа Рейнольдса зависит от условий входа в трубу, шероховатости ее стенок, отсутствия или наличия первоначальных возмущений в жидкости, конвекционных токов и др. При практических расчетах для круглых труб постоянного диаметра принимается Reкр = 2300.Безразмерный комплекс, представляющий собой произведение фактической скорости движения жидкости на диаметр трубы, деленное на кинематическую вязкость жидкости, является очень удобным параметром для характеристики режимов движения жидкости. Этот комплекс называется критерием или числом Рейнольдса, и обозначается Re = d/ (32) Таким образом, при Re Reкр движение жидкости происходит при ламинарном режиме, а при Re Reкр – при турбулентном режиме. Число Рейнольдса является важной характеристикой движения жидкости. Оно определяет относительную роль сил инерции и сил трения потока. При малых числах Рейнольдса вязкость жидкости оказывает существенное влияние на поток в целом, сглаживая возникающие в потоке мелкие пульсации скорости. При больших числах Рейнольдса преобладающее влияние оказывают силы инерции, действие которых приводит к передаче энергии от одного элемента потока к другому. Для трубопроводов и каналов некруглого сечения число Рейнольдса определяется по отношению к гидравлическому радиусу или эквивалентному диаметру по следующим формулам: Re = R/; Re = dэ/ (33) Учитывая, что R = d/4, для критического числа Рейнольдса, выраженного через гидравлический радиус, можно получить: Reкр = 2300/4 = 575 Таким образом, если R/ 575 – режим ламинарный, если R/ 575 – режим турбулентный. В трубопроводах систем отопления, вентиляции, газоснабжения, водоснабжения и др. движение, как правило, является турбулентным, так как движущаяся среда (вода, воздух, газ, пар) имеет малую вязкость. Ламинарный режим встречается значительно реже. Он наблюдается, например, при движении в трубах очень вязких жидкостей (масло, нефть, глицерин), при движении жидкостей в очень узких (капиллярных) трубках, в водоносных пластах. Вопросы к размышлению: К  акие виды гидравлических сопротивлений вы знаете? акие виды гидравлических сопротивлений вы знаете?Назовите виды движения жидкостей. Чем характеризуется турбулентное движение жидкости? От чего зависит критическое число Рейнольдса? Что определяет число Рейнольдса? 4. РезюмеИзучив учебный элемент, трубопроводчик линейный получил необходимый минимум знаний по основам гидравлики. 5.Контрольные вопросыЧто называется гидравликой? На какие классы разделяются жидкости? Назовите единицы измерения удельного веса? Что называется плотностью? Чем определяется удельный вес и плотность в производственных условиях? Дайте определение вязкости? Каким прибором определяется вязкость? Что понимается под идеальной жидкостью? Что называют гидростатикой? Какое гидростатическое давление называют абсолютным. Назовите единицу измерения гидростатического давления. Какими свойствами обладает гидростатическое давление? Что называется относительным покоем? Что показывает основное уравнение гидростатики? Какими свойствами обладают поверхности уровня? Сформулируйте закон Паскаля. На использовании закона Паскаля основано устройство, каких машин? Как определяется сила давления жидкости на плоскую стенку. Что изучает гидродинамика? Назовите гидродинамические характеристики потока. Какое движение называется установившимся? Что такое траектория? Назовите свойства элементарной струйки. Как разделяются потоки по характеру движения жидкости? Какие виды гидравлических сопротивлений вы знаете? Назовите виды движения жидкостей. Чем характеризуется турбулентное движение жидкости? От чего зависит критическое число Рейнольдса? Что определяет число Рейнольдса? 6.Литература1.Рабинович Е. З. Гидравлика. М., Недра, 1974. 2. Альтишуль А.Д, Киселев П. Г. Гидравлика и аэродинамика. М., Стройиздат, 1975. 3.Калицун В. И. , Дроздов Е. В. Основы гидравлики и аэродинамики, М., Стройиздат, 1980. 7.Слайдовый материалСлайд №1.Ареометр  Слайд №2 .Движения жидкости параллельными слоями 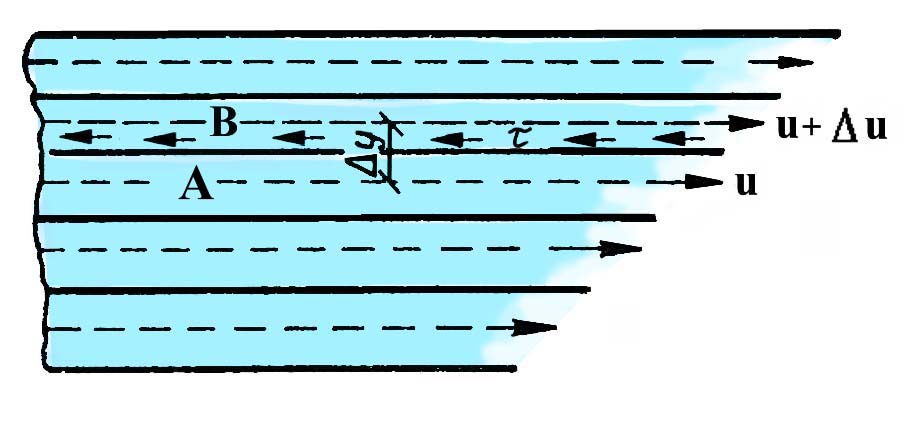 Слайд №3  Слайд №4  Слайд №5  Слайд №6  Слайд №7 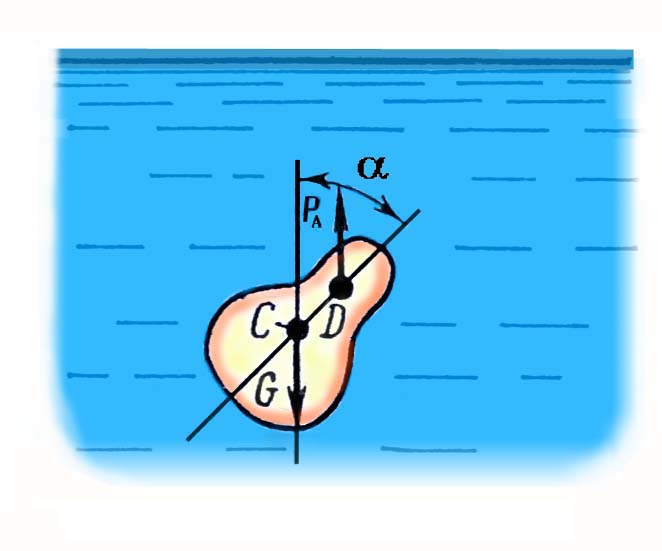 Слайд №8 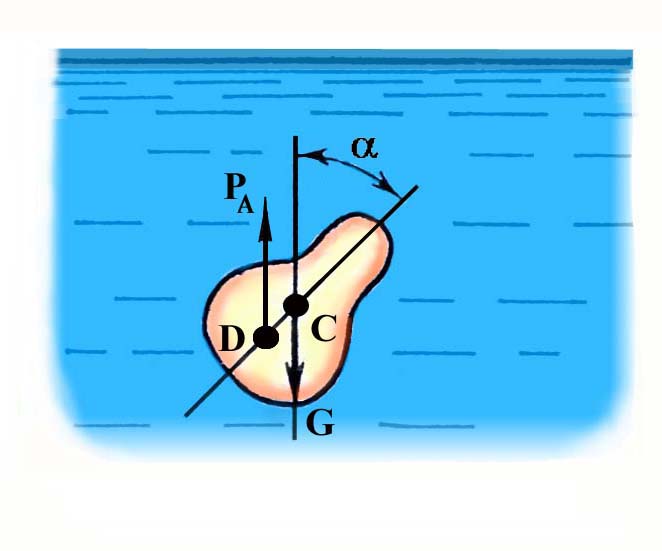 Слайд №9 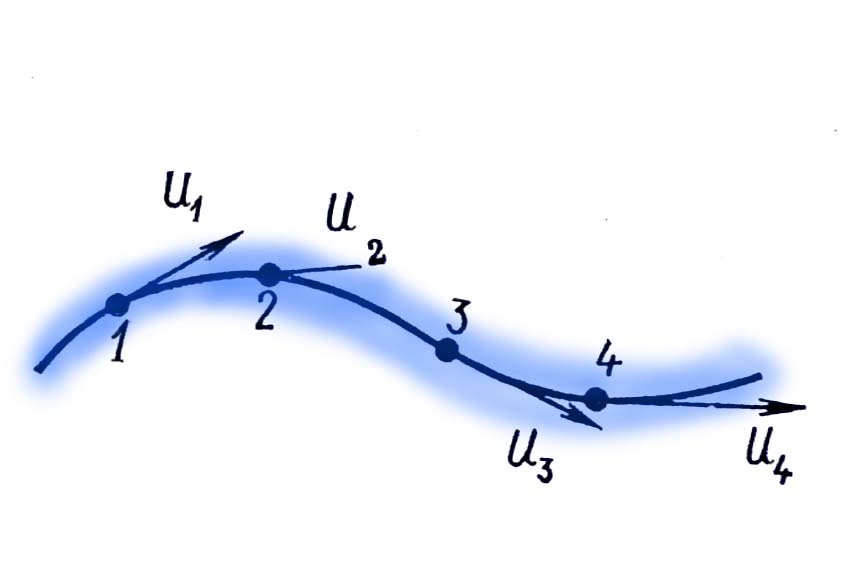 Слайд №10 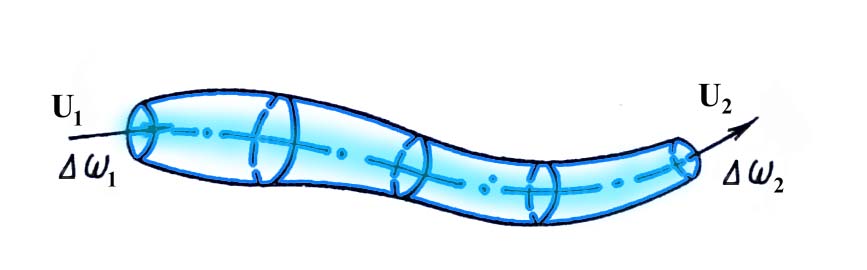 Слайд №11  Слайд №12  |
