Программа исследований

• Название: Программа исследований
• Дата: 22.04.2021
• Размер: 310 Kb.
• Имя файла: 33.doc
• Тип: Программа; #197565
• страница: 2 из 3

§ - толщина обшивки.

Формулы для определения , Мйу получены из формулы (1.2) пу­

*

тем замены а на /.

48

Для эпюр Му можно выделить два экстремума - положительный, вблизи центра плиты и отрицательный - на опоре, вблизи угла панели, вы­званный действием реактивной сосредоточенной силы. Следует однако за­метить что, отрицательные моменты в углах панелей при и > 2 в несколько раз меньше (по абсолютной величине) моментов в середине плиты и по­этому не представляют практического интереса при расчете реальных кон­струкций.

После обработки результатов расчетов методом наименьших квадра­тов получены формулы для определения изгибающих моментов в центре

панели

М х ^Ох^-п^С^-Ех ■> Му - МОуКпКсКЕу,

( \&2

где МОх =(1 + ух)—

М+,,Л

(2.31)

(2.32)



Кп =1 + 3,61



0,017С°’92

Кс =0,468 + 0,532

т и?

/! \ 0,0725 кЕх=\-

коэффициент, учитывающий влияние соотношения жесткостей элементов

панели;

коэффициент, учитывающий влияние погонной жесткости узлов сопряже­

ния панелей; здесь С - в кН/рад;

коэффициент, учитывающий влияние ортотропности материала обшивок на

величину изгибающего момента вдоль

оси х;

49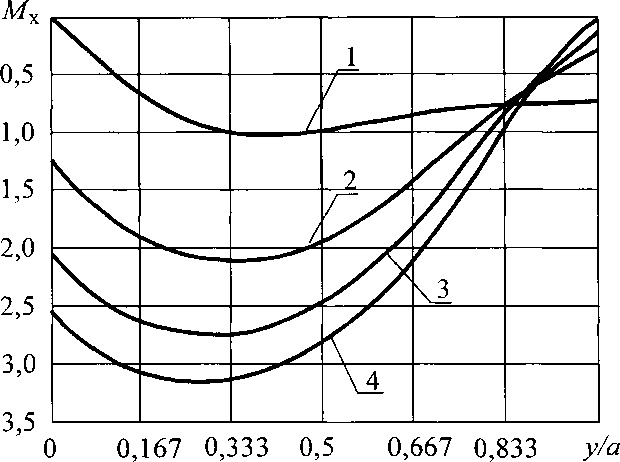

*



Рис. 2.7. Эпюры относительных изгибающих моментов Мх при различных п для С = 0, нагрузка распределенная (1- и = 0; 2 - п = 2,4; 3 - п = 4,8; 4 - п = 7,2)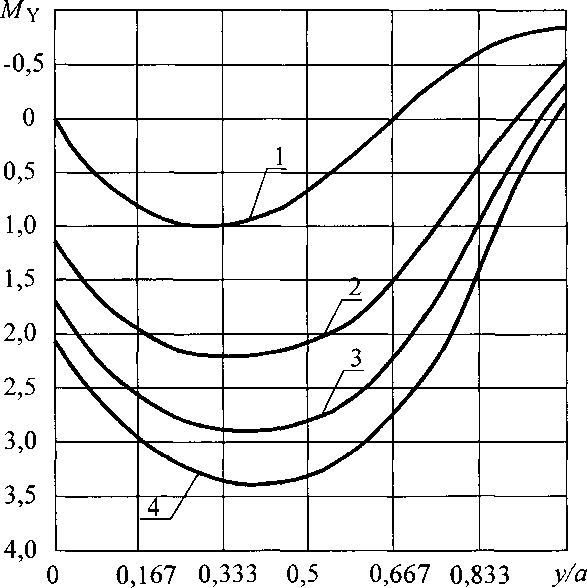




Рис. 2.8. Эпюры относительных изгибающих моментов Му при различных п для С = 0, нагрузка распределенная (1- /7 = 0; 2-/7 = 2,4; 3 - п = 4,8; 4 - п = 7,2)



50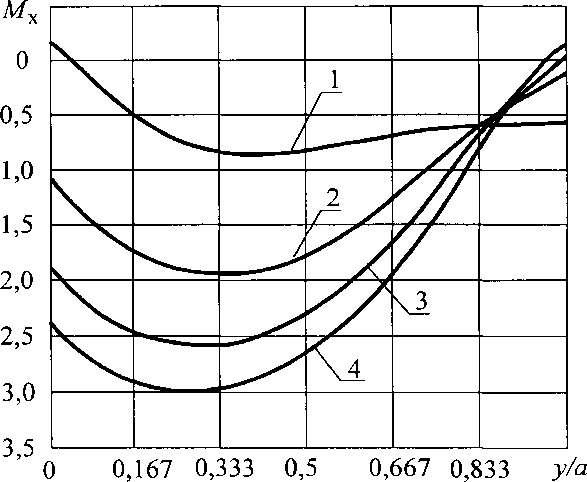





Рис. 2.9. Эпюры относительных изгибающих моментов Мх при различных п для С = 15 кН/рад, нагрузка рас­пределенная

(1- л = 0; 2 - п = 2,4; 3 - п = 4,8; 4 - п = 7,2)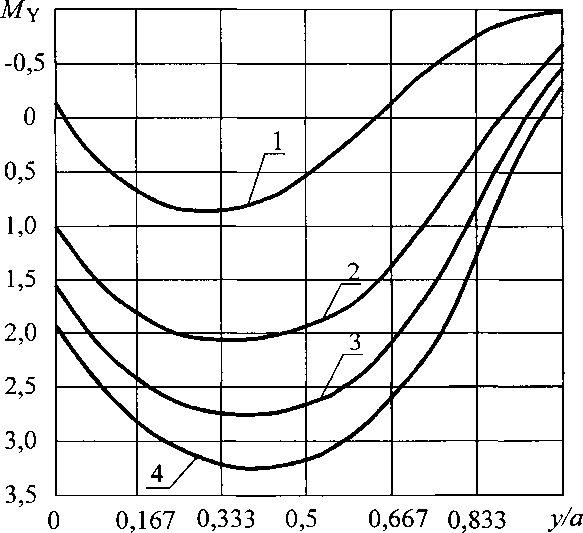




Рис. 2.10. Эпюры относительных изгибающих моментов Мх при различных п для С - 15 кН/рад, нагрузка распределенная

(1 - и = 0; 2 - п = 2,4; 3 - п = 4,8; 4 - п = 7,2)



51

К

Еу

= 1 +1,74 1 -

/^0,0425



коэффициент, учитывающий влияние ортотропности материала обшивок на величину изгибающего момента вдоль

оси у;

Анализ результатов расчетов показал, что максимальная величина изгибающих моментов, действующих на ребро также зависит в основном

от параметра п, влияние остальных параметров значительно меньше (рис. 2.11, 2.12). Максимальный изгибающий момент, действующий на ребро и максимальное нормальное напряжение в ребре можно определять по эм­пирическим формулам, параметры которых получены с помощью метода наименьших квадратов

(2.33)

(2-34)

где м°" = ^з’

К

-

т>
4д/з Ък2


х 1 X 0,0061с1

= 0,375 + 0,625 -

\е)

.0,98

, здесь С - в кН/рад;

х 0,585

Ке^=\,5 -0,5 -

\е)

здесь Ъ,к- соответственно ширина и высота сечения ребра.

52

1Й



Рис.2.11. Графики зависимости Мх/М^ от х/1 при раз­

личных п для С = 0, нагрузка распределенная

(1 - л = 0; 2 — п- 2,4; 3 — п — 4,8; 4 - п — 7,2)




Рис. 2.12. Графики зависимости Мх/М^ от п для С = О,

нагрузка распределенная

(1- п-0;2- п- 2,4; 3 - п = 4,8; 4 - п = 7,2)



53
Величина прогиба панели существенно увеличивается за счет до­полнительных деформаций, вызванных сдвигом среднего слоя панели. Влияние сдвиговых деформаций можно характеризовать параметром

I)

7 О3к-12
(2-35)

где Сг3 - модуль сдвига заполнителя (среднего слоя);

Суммарный прогиб в центре треугольной равносторонней шарнирно - опертой плиты определяем как сумму прогибов, определенных с учетом деформаций обшивок и деформаций сдвига среднего слоя (см. формулы (1.1)и(1.3))

4 2

7 9721) 21Ок

После подстановки а = / д/з/2 и алгебраических преобразований получаем

/ = ——(1 + 48т г )

17281)к 77

Ф

Выражение в скобках представляет собой по существу коэффициент увеличения прогиба вследствие деформаций сдвига среднего слоя.

На основании результатов проведенного исследования получена формула для определения максимального прогиба панели

/ = ^Кп/Кс/Кс/КЕ/,

(2.36)

где /0=^—

0 17281)

Кп/ = 1 + 12,6

1-

прогиб панели, вследствие деформации обшивок;

,0,68
/1 \ 0,057п
_ коэффициент, учитывающий влия­ние жесткостей элементов панели;

54

0,62	/ . х О.О39С0'68 !- -
	и?

— 1 + 48аи —

КЕ/

= 1 + 0,31 1-

/^0,465 и?

коэффициент, учитывающий влия­ние жесткости узлов сопряжения панелей;

коэффициент, учитывающий допол­нительный прогиб от сдвига средне­го слоя (заполнителя);

коэффициент, учитывающий орто- тропность материала обшивок;

здесь 5=



при Еу > Ех.

Проведенное исследование показало, что максимальная величина прогиба центрального узла панели в первую очередь зависят от параметра п, влияние же жесткости сопряжения узлов панелей (параметр С) значи­тельно ниже (рис. 2.13, 2.14).

На рис. 2.13, 2.14 величина относительного прогиба определялась

как

4

/

/ =

2.2.3. Напряженно-деформированное состояние панелей при действии монтажной нагрузки

При исследовании напряженно-деформированного состояния пане­лей при действии монтажной нагрузки количество варьируемых парамет­ров было увеличено на единицу. В качестве дополнительного был принят параметр

55




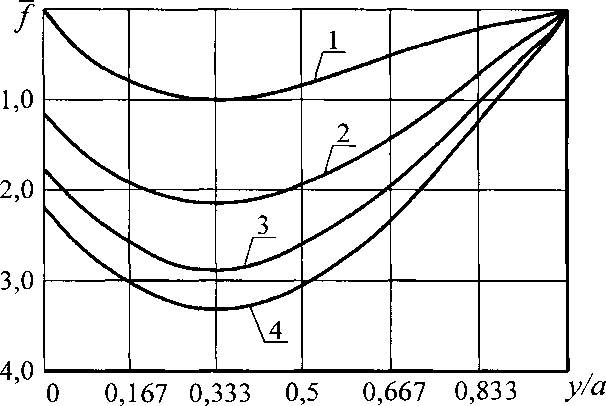
Рис. 2.13. Графики зависимости / от у/а при различных п для

С= О, нагрузка распределенная

(1- и = 0; 2 - п = 2,4; 3 - п = 4,8; 4 - п = 7,2)

4



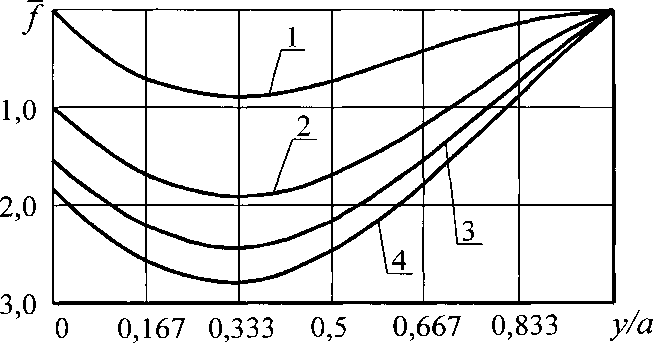
Рис. 2.14. Графики зависимости / от у/а при различных п для

С = 15 кН/рад, нагрузка распределенная

(1- и = 0; 2 - п = 2,4; 3 - п = 4,8; 4 - п = 7,2)

4

56




где <7 - диаметр круглой грузовой площади в центре панели, в пределах ко­торой прикладывалась нагрузка Р - 1,2 кН;

/ - длина стороны панели.

Расчеты панели выполнялись при трех значениях параметра Л — 0,232; 0,167; 0,0875.

После обработки результатов численного эксперимента методом наименьших квадратов получены формулы для определения максималь­ных изгибающих моментов в центре плиты при <7 < 0,232.

М1=М^К^, (2.37)

где Мрх=Р

мР _ иР кРкрКр

1У1у - 1У10у^п ^С^Еу’

Г(1 + уУ 3 А

' к х) 1пХ-0,379 +

(2.38)

4тг

—_ _|_ — 1

8тг 16я

(1-^х) , (З + Ух) .

1 г

8тг 16 л-
а

К? = 1 +1,03



=0,580 + 0,420

^\ 0,008с°’88

е)




при 5 > 0;

=1 + 4,56

л 1 \ 0,0265

при 5 > 0;



57

Значения Мдх и Мц получены в результате суммирования изги­

бающих моментов на границе круглой грузовой площади (см. формулы (1.4)) и изгибающих моментов для круглой пластинки диаметром с1, загру­женной равномерно - распределенной нагрузкой суммарная величина ко­торой равна Р. Последнее слагаемое в формулах получено из работы К.А. Китовера [47].

Максимальный изгибающий момент, действующий на ребро, и мак­симальное краевое напряжение в ребре панели рекомендуется определять по формулам


(2.39)

(2.40)

где


Р1

2Ък2’

= 0,276 + 0,579(1,15 - с$’6







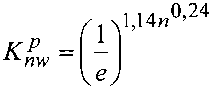
0,625-0,0945(<7-1,15)2

/^0,415

л \0,017С0,88

Исследование показало, что по сравнению с равномерно распреде­ленной нагрузкой изменение параметра п в меньшей степени влияет на из­менение напряжений в обшивках (рис. 2.15 - 2.18). Влияние параметра С практически не изменилось (рис. 2.17 - 2.18).

58

Изменение характера поперечной нагрузки сказалось на характере изменений изгибающих моментов в обшивках (рис. 2.15 - 2.18) и в ребрах (рис. 2.19), причем в последних можно выделить приопорные участки рав- Ь ные 0,25/ на которых изменение моментов происходит почти по линейно­

му закону (рис. 2.19).

Величина напряжений в ребрах при увеличении параметра и от 0 до 1,2 резко уменьшается при изменении параметра п до 2,4 до 7,2 напряже­ние в ребрах уменьшается незначительно (рис. 2.20).

Исследование по прогибам при действии монтажной нагрузки не производилось, т.к. при данном сочетании нагрузок ограждающие конст- ’Й рукции должны рассчитываться только на прочность.

Следует заметить, что величина максимальных напряжений в об­шивке в значительной степени зависит от параметра <7 (рис. 2.21, 2.22). В то же время изменение параметра с1 в рассматриваемых пределах (от 0,232 до 0,0875) оказывает существенно меньшее влияние на величину изги­бающего момента в ребре. При уменьшении <7 от 0,232 до 0,0875 момент в ребре увеличивается на 17%.

4 2.2.4. Напряженно — деформированного состояния панелей при

совместном действии продольных сил и поперечной нагрузки

Нелинейный расчет плиты выполнялся с применением шагового ме­тода, идея которого основана на отслеживании поведения системы при от­носительно малых приращениях нагрузки. При этом на каждом шаге ре­шалась линеаризованная система разрешающих уравнений для текущего приращения вектора узловых нагрузок, сформированного для рассматри­ваемого нагружения.

59





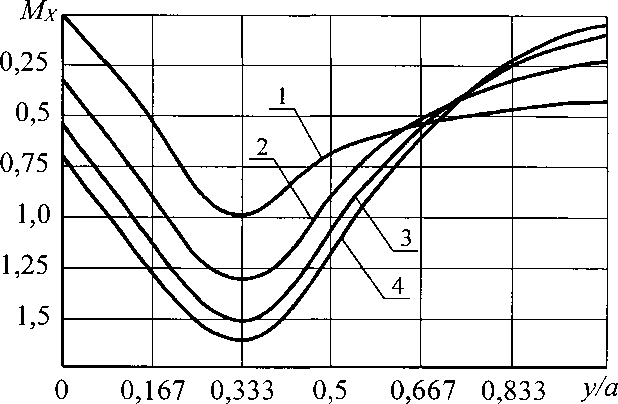
Рис. 2.15. Эпюры относительных моментов Мх при различ­ных п для С =0 и с1 = 0,232, нагрузка монтажная (1- л? = 0; 2 — п = 2,4; 3 - п = 4,8; 4 - п = 7,2)



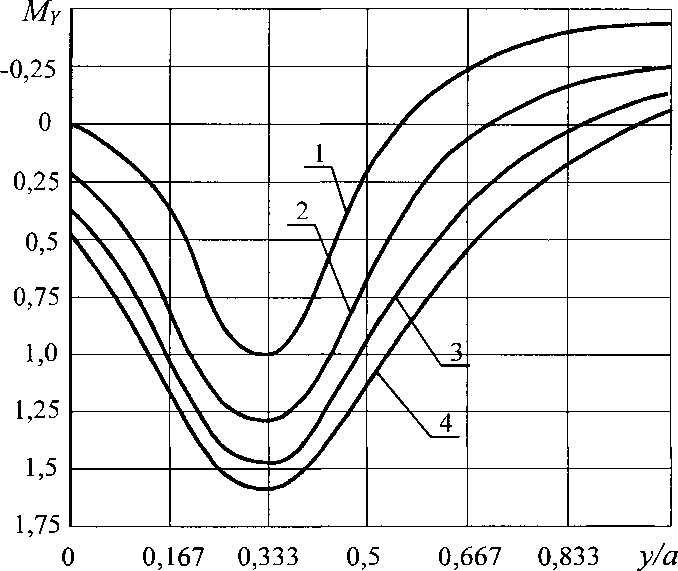
Рис. 2.16. Эпюры относительных моментов Му при различных

п для С = 0 и <7 = 0,232, нагрузка монтажная

(1- и = 0; 2 - п- 2,4; 3 -п = 4,8; 4 - п - 7,2)

60




Рис. 2.17. Эпюры относительных моментов Мх при различных п для С = 15 кН/рад и <7 = 0,232, нагрузка монтажная (1- и = 0; 2 - п = 2,4; 3 - п - 4,8; 4 - п = 7,2)



а

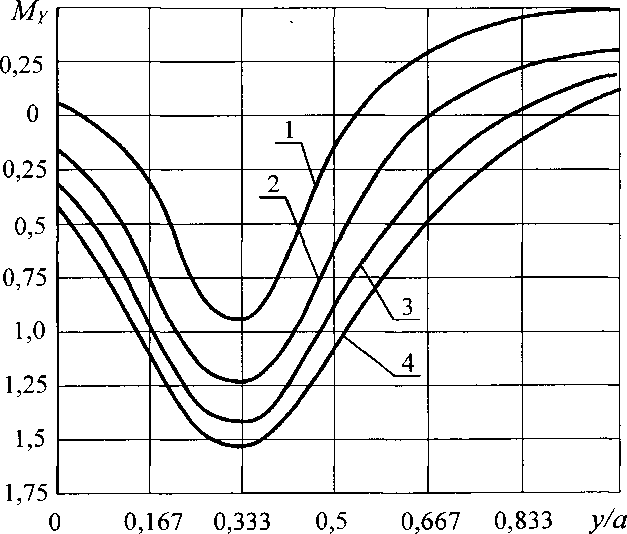
Рис. 2.18. Эпюры относительных моментов Му при различных

п для С = 15 кН/рад и с1 = 0,232, нагрузка монтажная

(1-и = 0;2-и = 2,4; 3 - п = 4,8; 4- п - 7,2)

61





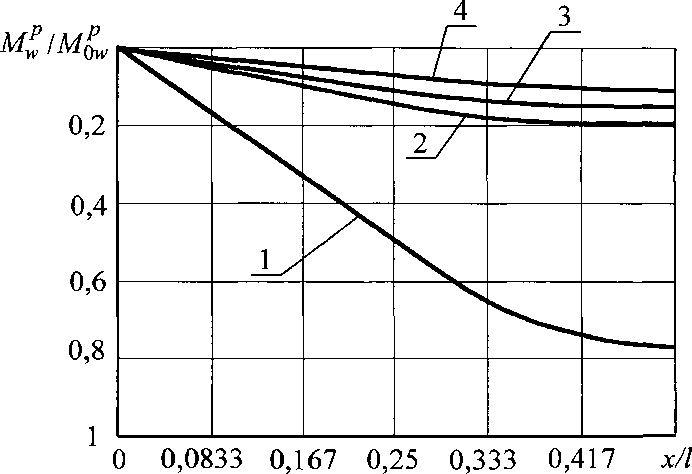
Рис. 2.19. Графики зависимости сгр от х/1 при различных п для

С = 0 и <7 = 0,232, нагрузка монтажная

(1 — п = 0; 2 - п — 2,4; 3 — п = 4,8; 4 — п = 7,2)



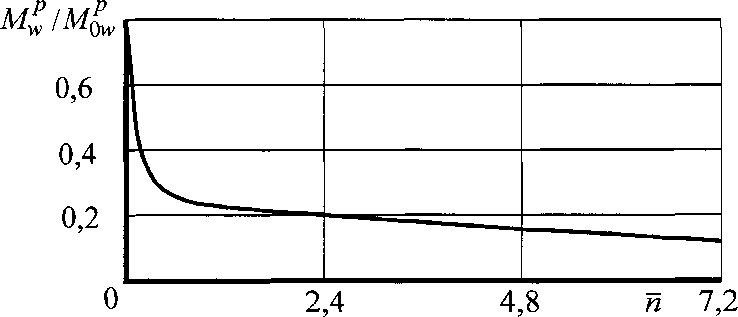
Рис. 2.20. Графики зависимостей М?/от п нагрузка монтажная <7 = 0,232,

62





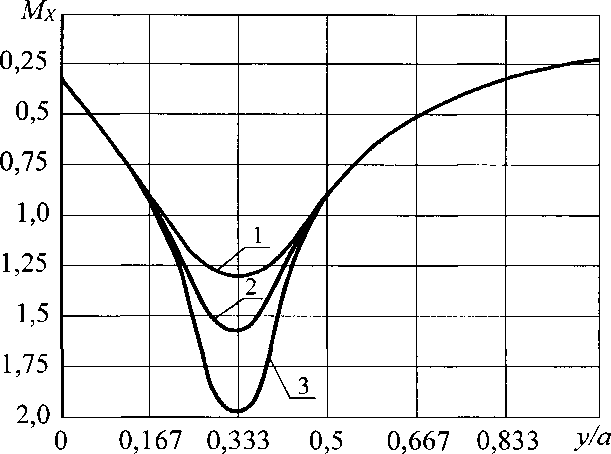
Рис. 2.21. Эпюры относительных моментов Мх при различных б/ для С = 0 и п = 2,4; нагрузка монтажная (1 - а = 0,232; 2 - 2 = 0,167; 3 - а = 0,0875)



Рис. 2.22. Эпюры относительных моментов Му при различных

а для С = 0 и п = 2,4; нагрузка монтажная

(1 - а = 0,232; 2 - а = 0,167; 3 - а = 0,0875)

63

В конце каждого шага производилось итерационное уточнение на­гружения за счет невязки в уравнениях равновесия, при этом на каждой итерации осуществлялась корректировка линеаризованной матрицы жест­кости.

С целью выбора необходимой конечно-элементной сетки и обосно­вания минимального числа шагов нагружения было проведено исследова­ние сходимости первого и второго рода.

При исследовании сходимости первого рода варьируемым парамет­ром являлось количество разбиений ребра панели по длине (параметр к). При исследовании сходимости второго рода во всех случаях к принима­лось равное 12, а менялось лишь количество шагов нагружения (параметр /). Сходимость результатов рассматривалась на примере главных растяги­вающих и главных сжимающих напряжений соответственно для нижней и верхней обшивок, а также на примере максимальных прогибов в центре панели.

Исследование сходимости первого рода показало, что для достиже­ния удовлетворительного решения (точность вычислений 1%) достаточно к = 10 - 12. Аналогичный результат мы находим в работе А.К. Гаврилова [24], в которой проводилось численное исследование трехслойной тре­угольной панели на поперечный изгиб.

Исследование сходимости второго рода показало, что для достиже­ния удовлетворительного результата достаточно 8-10 шагов нагружений, поэтому все расчеты выполнялись при / = 10.

В соответствии со СНиП П-25-80 модуль упругости древесины в расчетах конструкций на устойчивость и по деформированной схеме сле­дует принимать равным Е1 = 300Ес, что соответствует вероятному мини­мальному значению модуля упругости с обеспеченностью не ниже 0,99 [98]. Исходя из этого модуль упругости деревянных ребер был принят рав-

64

ным = 3007?с =3900МПа. Для полиэфирного стеклопластика отсутст­вуют необходимые рекомендации по назначению соответствующей харак­теристики, но учитывая приблизительно равные значения упругих свойств древесины и данного стеклопластика для обшивок был назначен рав­

ным

т Е 3900

Е^ = — Еоб = —— 6000 = 2340 МПа

00 Е 06 10000

По результатам расчетов для середины ребер и центра плиты опре­делялись коэффициенты