Программа исследований

• Название: Программа исследований
• Дата: 22.04.2021
• Размер: 310 Kb.
• Имя файла: 33.doc
• Тип: Программа; #197565
• страница: 1 из 3

33

ГЛАВА 2. ОПРЕДЕЛЕНИЕ НАПРЯЖЕННО - ДЕФОРМИРО­ВАННОГО СОСТОЯНИЯ ТРЕХСЛОЙНОЙ ТРЕУГОЛЬНОЙ ПАНЕЛИ СЕТЧАТОЙ ОБОЛОЧКИ ЧИСЛЕННЫМ МЕТОДОМ

Трехслойные панели, применяемые в сетчатых куполах во многих случаях изготавливаются в виде треугольников, близких к равносторонним (рис. 2.1). Такие панели имеют по периметру, как правило, обрамление в виде ребер к которым прикрепляются тонколистовые обшивки, между ко­торыми в свою очередь располагается средний слой. Ребра панелей выпол­няются из стеклопластиковых профилей или из цельнодеревянных бру­сков. Материалом обшивок служит в большинстве случаев стеклопластик толщиной 24-2,5 мм, имеются также отдельные примеры изготовления об­шивок из тонколистового алюминия. В качестве среднего слоя использует­ся пенопласт или сотопласт.

Воспринимая в составе купольного покрытия продольные и попе­речные нагрузки, трехслойные панели находятся в сложном напряженно- деформированном состоянии.

Под воздействием поперечной нагрузки трехслойные панели дефор­А мируются, и в них появляются дополнительные изгибающие моменты от

продольных сил. В этом случае имеет место геометрическая нелинейность. Известно также, что материалы, применяемые для ребер панелей, имеют нелинейную зависимость между деформациями и напряжениями (физиче­ская нелинейность).

Общая картина напряженно-деформированного состояния плиты дополнительно усложняется тем обстоятельством, что один из наиболее неблагоприятных вариантов нагрузки является нагрузка в виде монтажно­го сосредоточенного груза. При такой нагрузке, как отмечается в работе [58], применение гипотезы о несжимаемости среднего слоя не позволяет

34

получить удовлетворительного описания деформаций вблизи места распо­ложения силы.

Аналитическое решение задачи расчета трехслойных треугольных плит даже с учетом упрощающих предположений представляется возмож­ным только в численном виде.

2.1. Программа исследований

Для определения варьируемых параметров численного эксперимента выделим факторы в наибольшей степени влияющие на напряженно- деформированное состояние (НДС) трехслойных панелей.

Первый фактор - это отношение жесткостей обшивок и ребер пане­лей. Рассмотрим равностороннюю треугольную трехслойную панель с длиной ребра /, шириной ребра Ь, толщиной среднего слоя и обшивок со­ответственно А и 8 (рис. 2.1).



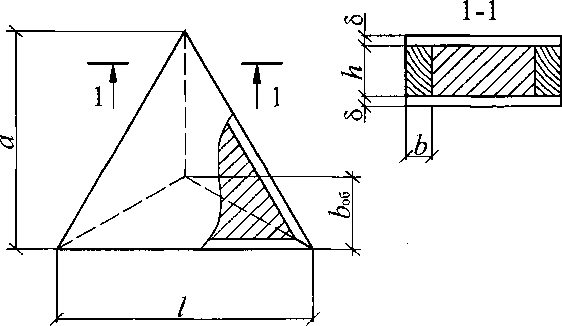
Рис. 2.1. Схема трехслойной панели купола

Выделим в этой панели треугольный фрагмент шириной &об, вклю­

чающим одно ребро с примыкающими к нему обшивками и средним сло­

ем. Отношение изгибных жесткостей обшивок и ребра равно

35

Яоб'об _ Дэб ^об^/2)2 _ 6ЕобЬоб8

ЕрЬк
*

Обозначим

(2.1)
п _ ^Еоб1д

ЕрЪк ’

(2-2)

тогда с учетом того, что &об = //2д/3, формулу (2.1) запишем в виде

^об _

Ер1р 2

(2-3)

Используя формулу (2.2) запишем аналогичное выражение, равное

отношению продольных жесткостей обшивок и ребра

Еоб ^об _ 1

ЕрАр 2Д

(2-4)

Исходя из анализа формул (2.3) и (2.4), примем в качестве первого варьируемого параметра п, характеризующего отношение жесткостей об­шивок и ребер.

Второй фактор - это отношение поперечной и продольной нагрузок, действующих на панель.

Рассмотрим пологую шестиугольную пирамиду, расположенную в вершине купола (рис. 2.2а). В виду малости угла а будем считать, что па­нели, образующие пирамиду равносторонние. Предположим, что все про­дольные силы, действующие на панель, передаются через торцы ребер. Поперечную равномерно - распределенную нагрузку обозначим через Предположим, что на одно ребро передается поперечная нагрузка с грузо­вой площади шириной Ьо5, тогда на ребро будет действовать треугольная поперечная погонная нагрузка, максимальная величина которой равна

=0,5^-/-1ё30° (2.5)

Максимальный изгибающий момент действующий на ребро равен

36



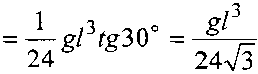
(2.6)



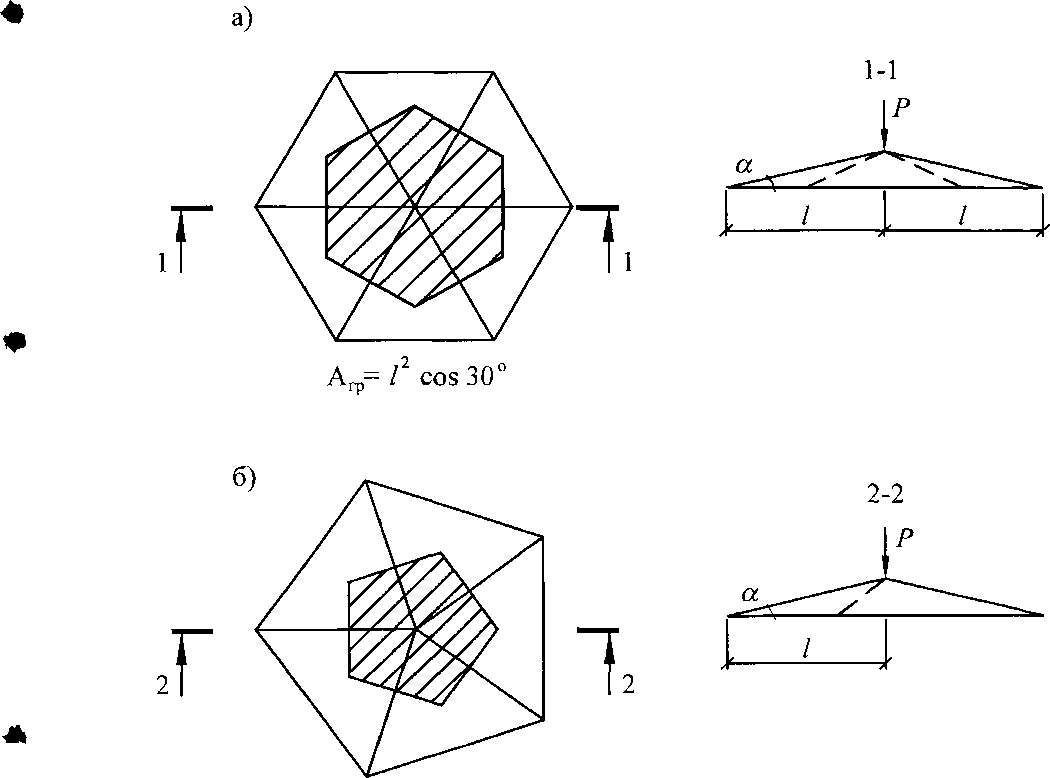
Рис. 2.2. Расчетные схемы пологих пирамид,

м =

используемые при определении I.

а) шестиугольная пирамида

б) пятиугольная пирамида (штриховкой обозначена грузовая площадь Агр, с которой собирается нагрузка при определении Р).

37

При определении продольных усилий, действующих в ребрах пане­лей, будем считать, что поперечная нагрузка прикладывается в узлах пи­рамиды в виде сосредоточенной силы Р, равной

Р = #72соз30° (2.7)

Продольное усилие, действующее на торец одного ребра панели

равно

^рп =

р

12зта

§12соз30°

12зта

(2-8)

Обозначим через I относительный эксцентриситет равный

М

I —

(2-9)

тогда с учетом (2.6) и (2.8) окончательно получаем

1 I .

I = —зта

3 к

Рассматривая пятиугольную пологую пирамиду (рис. 2.2 б) и прово­дя аналогичные преобразования, получаем точно такую же формулу для

определения относительного эксцентриситета.

Принимаем в качестве второго варьируемого параметра относитель- «Л ный эксцентриситет I.

Третьим фактором, оказывающим существенное влияние на напря- женно-деформируемое состояние панели является степень упругого за­щемления сторон панелей в зоне примыкания двух смежных панелей.

Рассмотрим узел сопряжения двух смежных панелей купола, в кото­ром наиболее часто используются болты, поставленные с шагом <яб (рис. 2.3 а).

Предположим, что на узел действует погонный изгибающий момент М, тогда в болтах будут возникать растягивающие усилия N5, а на внут­

38

ренних гранях ребер на полосе высотой х будет действовать сминающее напряжение, максимальное значение которого будет равно сг^ (рис. 2.3 б).



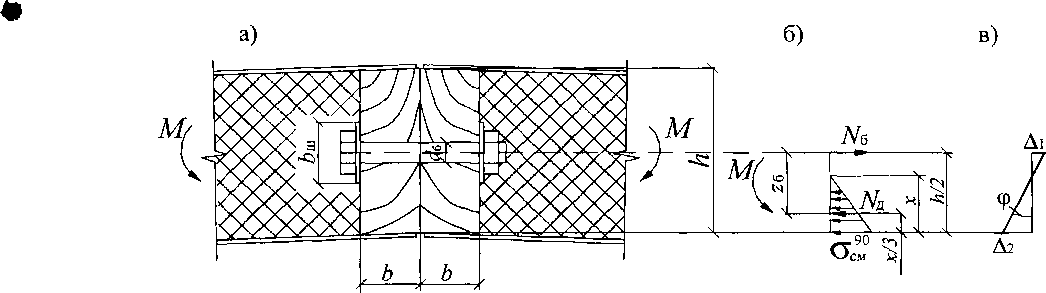
Рис. 2.3. К определению коэффициента погонной жесткости С

узла сопряжения панелей:

а) конструкция узла;

б) схема усилий, действующих в узле;

в) эпюра деформаций в узле.

Рассмотрим деформации, возникающие в узле (рис. 2.3 в). Деформа­ции в уровне болта будут складываться из деформации собственно болта и деформации обмятая древесины поперек волокон, возникающих в зоне контакта древесины и шайбы:

А1 - + Ад

45м^90

М ■ а^Ъ ■ АЕ

2б

(2-11)



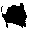
N 2

где М = ——— - погонный изгибающий момент; «б

«б - шаг постановки болтов;

Ъ - ширина ребра;

к х

плечо внутренней пары сил

39

АсмЕдп + А^ЕС

АЕ = относительная жесткость болтового соединения;

Асм^бЕ90Ес

*

здесь А“м - площадь смятия под поверхностью шайбы;

Аб - площадь поперечного сечения болта;

Е9о - модуль упругости древесины поперек волокон;

Ес - модуль упругости стали.

Абсолютная деформация в уровне нижней плоскости ребра равна

о?°ь _ 2М-Ь

*

(2-12)

А 2 — — ,

^90 Е90абх Е90х ’ 2б

где Ад- суммарное сжимающее усилие, действующее поперек во-

локон древесины;

х - высота сжатой зоны.

Высоту сжатой зоны определяем из соотношений деформаций А2 и

А1-

2х

А + А2

^2

отсюда
2 , А1 + А

Л2 Л

+ /А2>

(2.13)

После подстановки в формулу (2.13) значенийЛ1 и А2 получаем квад­

ратное уравнение вида

'Т.К АЕх + 4х — И — О

(2-14)

где КАЕ - Е90<яб

^см-^90 +

< 4гм^б^90^с >

*

Единственное положительное решение этого уравнения имеет вид

— 4 + д/16 + %КАЕк

х =

(2-15)

^ЕАЕ

40



При малых значениях угла поворота ребра относительно вертикаль­ной плоскости, угол поворота можно представить как

= 2(А1 +Л2)

* к

Определим коэффициент погонной жесткости узла сопряжения па­нелей в виде




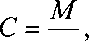
<Р

(2-17)

Тогда, с учетом формул (2.11), (2.12) и (2.16), после алгебраических

преобразований получаем окончательную формулу для определения С.



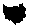
Е9О/2 • х(ЗЛ — 2х)

12Ъ(К + 2)

(2-18)

Четвертым фактором, влияющим на напряженно - деформированное состояние панелей является ортотропность свойств материала обшивок в случае применения в качестве обшивок фанеры. Исходя из этого четвер­тым варьируемым параметром принят безразмерный параметр



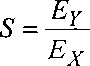
приЕг>Ех (2.19)

где Ех - модуль упругости материала обшивки в направлении оси X;

Еу - модуль упругости материала обшивки в направлении оси У;

При действии монтажной нагрузки величина напряжений и прогибов будет во многом зависеть от величины грузовой площади, на которой дей­ствует монтажный груз Р = 1,2 кН, потому в качестве пятого варьируемого параметра принят относительный диаметр грузовой площади

. 5 = р (2.20)



где (1- диаметр грузовой площади на которой действует монтажный груз;

I - длина стороны панели.

российская

41 . ,)( уддрСТВЕННАЯ

ниБ ЛИО I НКл

Определим наиболее вероятные границы изменения варьируемых параметров на примере существующих конструкций. В качестве первого примера выберем купольное покрытие диаметром 10 м, возведенное в Се­веродонецке [59]. Поверхность купола является частью 720-гранника, для панелей, образующих верхнюю пятиугольную пирамиду зта=0,0875.

Панели купола имеют обшивки толщиной 2,5 мм, выполненные из стеклопластика, средний слой толщиной 75 мм изготовлен из кольцепла- ста, длина ребра 1260 мм, ширина 20 мм. Принимая отношение модуля уп­ругости материала обшивок к модулю упругости материала ребер равным 0,5, получаем величину первого параметра

2-0,5-1260-2,5 и = = 2,1

20-75

второй параметр равен

1260-0,0875 =

3-75

В качестве второго примера рассмотрим купольное покрытие выста­вочного павильона в г. Лейк (Швейцария) [111, 118]. Данное купольное покрытие образовано на основе 320-гранника, для верхних панелей зта = 0,126. Длина ребра 231 см, толщина среднего слоя 50 мм, обшивок 2 мм. Первый параметр равен

2-0,5-2310-2

и = — 7,1

13-50

второй параметр равен

,= 2310-0,!26 = 1>94

Анализ конструктивных решений куполов собранных из трехслой­

ных панелей показал, что наиболее вероятные значения варьируемых па­

раметров находятся в пределах п = 2,0 4- 7,0; I = 0,5 4- 2,0; С = 54-25 кН/рад;

42

2.2. Расчетная схема и методика проведения численного эксперимента

В ходе численного эксперимента проводилось исследование напря­женно-деформированного состояния равносторонней треугольной панели (рис. 2.1). Длина стороны равносторонней панели принималась равной 1600 мм, толщина среднего слоя - 50 мм.

В качестве материала обшивок был выбран наиболее дешевый и распространенный вид стеклопластика - полиэфирный, имеющий Еоб = 6000 МПа и обладающий изотропными свойствами. Для ортотропных об­шивок были приняты следующие характеристики: Ех - 4000 - 4800 МПа, Еу = 7200 - 8000 МПа, что примерно соответствует упругим характеристи­кам трехслойной фанеры толщиной 3-4 мм. В расчетах предполагалось что ребра выполнены из древесины, модуль упругости которой равен Ер = 104МПа.

Численный эксперимент проводился на основе метода конечных элементов с использованием программы 8САЭ. Расчетная схема панели показана на рис. 2.4. Ребра панели разбивались на плоские прямоугольные конечные элементы (КЭ), обшивки - на плоские треугольные КЭ и сред­ний слой - на пространственные КЭ в виде треугольных призм.

Выбор принятой расчетной схемы панели базировался на основе следующих предположений:

а) обшивки панели работают на двухосное растяжение (сжатие);

б) изгибная жесткость ребер в плоскости ХОУ равна 0;

в) ребра панели свободно деформируются в направлении оси X.

Для моделирования узла сопряжения панелей с различной степенью упругого защемления в расчетную схему были введены вспомогательные стержни и балки, которые в то же время не препятствовали свободному

43

перемещению панелей в горизонтальной и вертикальных плоскостях. Же­сткость балок была назначена примерно в 1 000 раз больше жесткости эле­ментов панели в соответствии с рекомендациями, изложенными в [60].

4




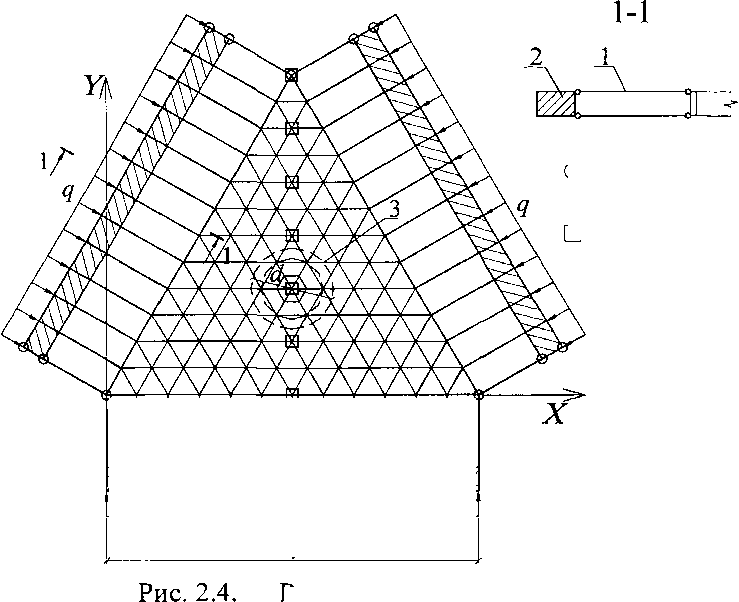
Расчетная схема панели

О - закрепление узлов по оси 2

□ - закрепление узлов по оси X

7/		7/		//х	7/		7^	7х	<7	7/	>7
я , 1

1 - вспомогательные стержни;

2 - вспомогательные балки;

3 - круглая грузовая площадь диаметром <7.

Расчеты выполнялись при ширине ребра Ъ — 13,3, 20 и 40 мм, что со­ответствует значениям п = 7,2; 4,8; 2,4. исследование влияния ортотропных свойств обшивок проводилось при 5=0; 0,25; 0,5; 0,75; 1,0. Степень упру­гого защемления узлов панелей оценивалась при С = 0; 5; 15 и 25 кН/рад. Расчеты на монтажную нагрузку Р = 1,2 кН проводились при <7 = 0,0875; 0,167; 0,232.

Поперечная равномерно - распределенная нагрузка на панель опре­делялась исходя из предположения того, что отношение высоты оболочки

44

к ее диаметру больше чем 0,31. При таком соотношении размеров оболоч­ки величина поперечной нагрузки, определенная по СНиП 2.01.07-85 с учетом изменения № 2 для V снегового района будет равна

< ё = .ц = 3,2-0,4 = 1,28кПа.

В ходе численного эксперимента продольные силы прикладывались к панели в виде погонной равномерно - распределенной нагрузки по пери­метру панели. Погонная нагрузка д определялась из выражения

ё-12

12/ • к

полученного из формул (2.6) и (2.9).

Ж

2.2.1. Характер напряженно - деформированного состояния трехслойной треугольной панели сетчатой оболочки при действии продольных сил

Проанализируем картину распределения усилий во вспомогательных стрежнях, т.е. по существу картину распределения усилий в зоне взаимо­действия двух смежных панелей. Эта картина характеризуется очень не­равномерным распределением усилий по длине панели, причем концен­трация усилий зафиксирована в углах панели. Установлено, что для реаль­ных конструкций от 35% до 59% всех продольных усилий передаются на панель в угловых зонах.

Наибольший интерес представляют величины усилий в ребрах и на­пряжений в обшивках панели. При отсутствии обшивок и при 5=0 макси­мальное усилие в ребре панели равно

А Г2'22)

45

и наоборот, при отсутствии ребер максимальное напряжение

в обшивке

равно

41

^.тах тах 7

сг = сг = —

х у 28

(2.23)

Обозначим через N относительное усилие в ребре равное

- 2^Х„

™ ДАтах ’

(2.24)

а через сг х(у) - относительное напряжение в обшивках, равное

(2.25)

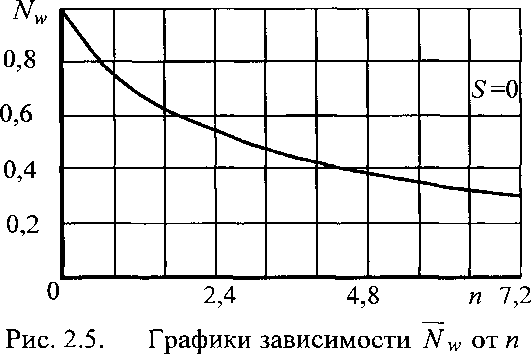
На рис. 2.5 и 2.6 показаны графики зависимостей и

СГх(у) ОТ П.

При и —> со асимптотически приближается к 0, <Ух(у) - к 1 [64]. Влия­

ние параметра 8 на величину усилий существенно меньше. Так, измене­
ние параметра 8 от 0 до 1 приводит к увеличению усилия в ребре на 14% и напряжений в обшивке (су) на 28%.

После обработки результатов вычислений методом наименьших квадратов получены формулы для определения усилий в ребрах жения в обшивках панелей.
и

напря-

,0,65

сгх = —

х 28

1-

л ^\0,34п

/1 X 0,034и0’65

0,65

1-

л^хДОЩЗ'0’81

\е)

/^0,3 ЗЯ0’86

(2.26)

(2.27)

>

х0,034и0’65

(У у = — у 28

(2.28)

1-

46

*

- д1г- '	т	0,34и°’65 4-	1-Ш	0,34и°’65	Л 1-
№ 2-Л					1

шах

"ч



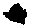
0,0915°’81



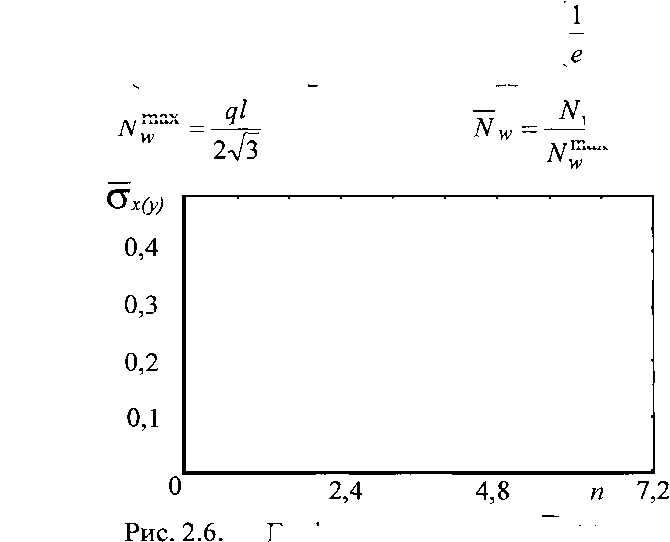
Графики зависимости сгх(^) от п

/^ОДШи0’65

! \ 0,3350’86

е)

ТУ тах

						5=0

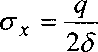
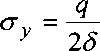
СГ

тах 28

>

1-

\е)

]\0,034и

,0,65 Т

2-


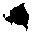
0,335°’86


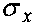
(т)

^(у)

^тах

47

2.2.2. Напряженно - деформированное состояние панелей при действии равномерно распределенной поперечной нагрузки

Исследования напряженно - деформированного состояния панели на действие поперечной нагрузки выполнялись при различных комбинациях параметров п, С, 8. Расчеты производились при п равном 0; 2,4; 4,8; 7,2, при С равном 0, 5, 15, 25 кН/рад и при 8 = 0; 0,5; 1,0 [69]. На рис. 2.7. - 2.10. приведены эпюры относительных моментов Мх и Му вдоль оси симметрии панели при различных п и С.

Относительные моменты М х и М у определялись по формулам

— м Мх=—^, (2.29)

М0х

— Му Му=—^ (2.30)

Моу

где Мх, Му - изгибающие моменты соответственно в плоскостях ХОХ и УОХ;

мох =(1 + ^)^-,

< 2

МОу =(1 + уу)^-

здесь § - поперечная нагрузка на панель;

I - длина стороны панели;

к - толщина среднего слоя;