Программа исследований
 Скачать 310 Kb. Скачать 310 Kb.
|
|
Му м* где - изгибающий момент в ребре, определенный без учета действия продольной нагрузки д; -изгибающий момент в ребре, определенный по деформируемой схеме - с учетом действия продольной нагрузки д; Мх, Му - изгибающие моменты в центре плиты соответственно в направлении осей х и у, определенные без учета действия продольной нагрузки д; изгибающие моменты в центре плиты соответственно в направ лении осей х и у, определенные по деформируемой схеме - с уче том действия продольной нагрузки д. 65 На рисунках 2.23 - 2.24 показаны графики изменения коэффициентов 2, в зависимости от I при различных п. При увеличении нагрузки д (что соответствует уменьшению I) значения 2, уменьшаются, чего и следовало ожидать. При уменьшении д (увеличении I) значения 2, асимптотически приближаются к единице. Увеличение параметра п (при фиксированном отношении 1[к) также приводит к уменьшению 2,. Значения для ребра можно определять по формуле (30) СНиП II- 25-80 N (рВ-с -^бр-^-Л (2.41) где Убр - площадь брутто поперечного сечения ребра панели; - коэффициент, учитывающий подкрепляющее влияние обшивок, определяемый по формуле 1 лр1,О4и°’07’
(2.42) Легко заметить, что для изотропных обшивок (для 5=0) при п —> 0 коэффициент Ка становится равным 1. Для треугольной трехслойной пластины с изотропными обшивками запишем выражение для коэффициента 2, в виде <^ = 1- — (2.43) &сг где с - напряжение в обшивке; сус, - критическое напряжение в обшивке. Величину критического напряжения получим из известного выраже- • ния треугольной пластины [101]. 66 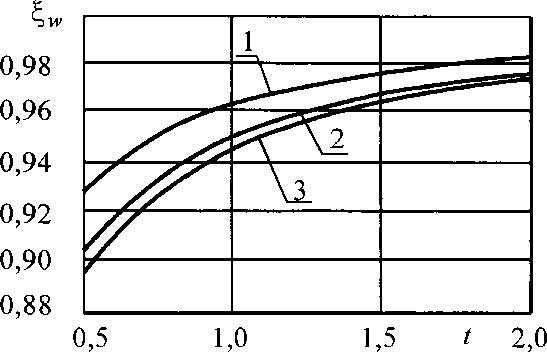 Рис. 2.23. Графики зависимостей от I при различных п, обшивки изотропные (1 - п = 2,4; 2 - п = 4,8; 3 - п — 7,2) Ж 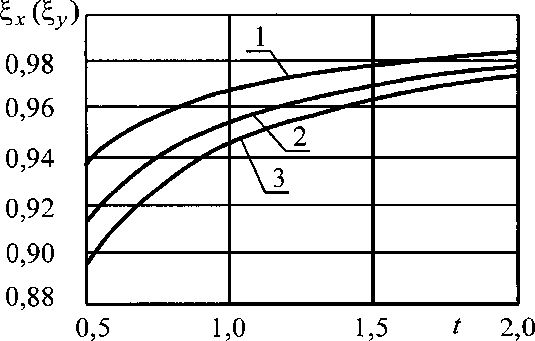 Рис. 2.24. Графики зависимостей (^)от I при различных п, обшивки изотропные (1 -п = 2,4; 2 - п = 4,8; 3 - п = 7,2) 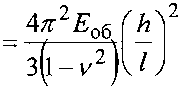 (2.44) а В окончательном виде формулы для определения примут вид 67 ^'хУу)Ктх 4тг2ЕхКсгп х^ у}^ ту 4тг2 ЕуКсгп "Л2 1^7 (2-45) (2-46) где стх, (5У -напряжения в обшивке от действия продольной нагрузки соответственно в направлении осей х, у, определяемые по формулам (2.27) и (2.28); В Ех, Еу - вероятные минимальные значения модулей упругости материала обшивки соответственно в направлении осей х и у; ух, Уу - коэффициенты Пуассона материала обшивки с обеспеченностью 0,99 соответственно в направлении осей х и у; I - длина стороны панели; к - толщина среднего слоя; Кт Кту- коэффициенты, учитывающие влияние деформаций сдвига среднего слоя соответственно в направлении осей х и у, определяемые по формулам ^=1+48^; (2.47) Кту = 1 + 48гау; (2.48) здесь тх, ту - коэффициенты, характеризующие соотношение изгибных и сдвиговых жесткостей соот ветственно в направлении осей х и у, опреде ляемые по формулам Ех8к тх = —( \ у 2(1-к^)Оз/2 а Еу8-к 2(1 (2.49) (2.50) 68 Ксгп- коэффициент, учитывающий граничные условия трехслойной пластины, определяемый по формуле 1 тйи0,04 (2-51) Ф Ф 2.3. Оценка напряженно - деформированного состояния панелей при варьировании исследуемых факторов. Выводы по второй главе. Для оценки достоверности проведенного численного эксперимента было проведено сопоставление полученных результатов с аналогичными результатами, полученными А.К. Гавриловым [24 - 29]. В этой работе приводятся данные по напряженно - деформированному состоянию трехслойной треугольной плиты с длиной ребра 7=1,74 м. Ребра сечением 40x80 мм выполнены из древесины, а обшивки толщиной 1 мм - из алюминиевого сплава. Нагрузка на панель равномерная § = 1,5 кПа. По формуле (2.2) определяем параметр п Ео61-8 _ 2-7,1-Ю4 -1740-1 ЕрЬ-И 104-40-80 104-40-80 По формуле (2.34) определяем напряжение в ребре при -1 и = 1, т.к. обшивка изотропная и нет защемления на опорах. = 4,46 • 0,300 • 1 -1 = 1,34 МПа = 0,300 69 По данным А.К. Гаврилова напряжение в ребре равно 1,3 МПа, расхождение составляет 3%, что вызвано погрешностями при обработке данных численного эксперимента. # В результате численного эксперимента получены следующие ре зультаты 1. На основе анализа существующих и запроектированных куполь ных покрытий определены области наиболее вероятных значений варьируемых параметров. Параметр и, характеризующий соотношение жесткостей обшивок и ребер изменятся в пределах от 2,0 до 7,0, относительный эксцентриситет ? - от 0,5 до 2,0, коэффициент погонной жесткости узла соф пряжения панелей - от 5 до 25 кН/рад. 2. Выявлены зависимости напряженно - деформированного состояния панели от величины варьируемых параметров. Установлена степень влияния варьируемых параметров на НДС панели для двух видов нагрузки. При равномерно - распределенной нагрузке наибольшее влияние оказывает параметр п, при монтажной нагрузке - параметры (Лип. 3. Проведено численное исследование панели при совместном действии продольной и поперечной нагрузок с учетом геометрической нели- ф нейности. Получены эмпирические зависимости для коэффициентов по зволяющие рассчитывать элементы панели по деформированной схеме. | |||||||||||||||
