Программа по дисциплине Теоретические основы электротехники

• Название: Программа по дисциплине Теоретические основы электротехники
• Анкор: Uchebnoe_posobie_po_elektrotekhnike_SPO.doc
• Дата: 10.05.2017
• Размер: 5.49 Mb.
• Имя файла: Uchebnoe_posobie_po_elektrotekhnike_SPO.doc
• Тип: Программа; #7400
• страница: 4 из 8

1) Основные определения

 В линейной электрической цепи сопротивления ее элементов не зависят от величины или направления тока или напряжения.

Вольтамперные характеристики линейных элементов  (зависимость напряжения на элементе от тока)  являются прямыми линиями (рис. 22.7).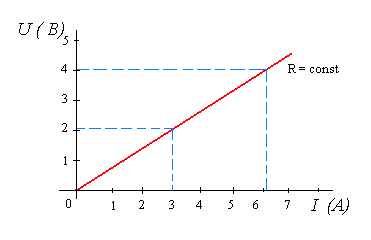



Рис. 22.7

Определим величину линейного сопротивления по характеристике (см. рис. 22.1.)



Таким образом, значение линейного элемента не зависит от изменения напряжения и тока

       В нелинейной электрической цепи сопротивления ее элементов зависят от величины или направления тока или напряжения.
 

  Нелинейные элементы имеют криволинейные вольтамперные характеристики, симметричные или несимметричные относительно осей координат.  

  Сопротивления нелинейных элементов с симметричной характеристикой не зависят от направления тока.
      

Сопротивления нелинейных элементов с несимметричной характеристикой зависят от направления тока. Например, электролампы, термисторы имеют симметричные вольтамперные характеристики (рис. 22.2), а полупроводниковые диоды - несимметричные характеристики (рис. 22.3).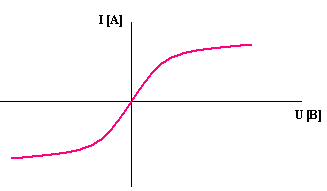



                                                                           

Рис.22.8. Вольтамперная симметричная характеристика нелинейного элемента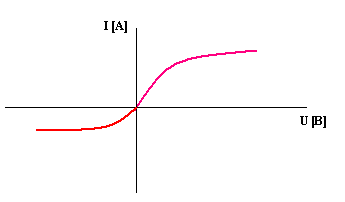



      

Рис.22.9. Вольтамперная несимметричная характеристика нелинейного элемента

2) Графический метод расчета нелинейных цепей постоянного тока

       Известные аналитические методы непригодны для расчета нелинейных электрических цепей, так как сопротивления нелинейных элементов зависят от направления и значения тока или напряжения.

Применяются графоаналитические методы, основанные на применении законов Кирхгофа и использовании заданных вольтамперных характеристик (ВАХ) этих элементов. Рассмотрим электрическую цепь, состоящую из двух последовательно соединенных нелинейных сопротивлений н.с.1 и н.с.2 (рис. 22.4).

ВАХ 1 и ВАХ 2 приведены на рис. 22.5.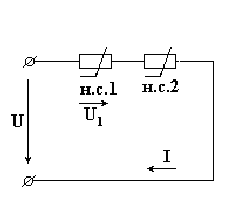



Рис. 22.10. Схема электрической цепи из двух последовательно соединенных нелинейных сопротивлений

      К цепи подведено напряжение U, и оно равно сумме падений напряжений на н.с.1 и н.с.2:

     

      По всей цепи протекает один и тот же ток I, так как н.с.1 и н.с.2 соединены между собой последовательно.

Для определения тока в электрической цепи нужно построить результирующую ВАХ цепи.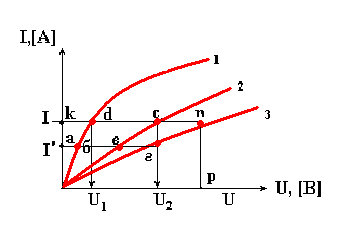



Рис. 22.11. Вольтамперная характеристика электрической цепи из двух последовательно соединенных нелинейных сопротивлений

Для построения этой характеристики следует суммировать абсциссы кривых 1 и 2

(аг = аб + ав), соответствующие одним и те же значениям тока.

Далее, задаваясь произвольным значением тока (например, больше I' и меньше I' ) можно построить ВАХ всей цепи (рис. 22.11, кривая 3).

Затем, пользуясь этой ВАХ, можно найти искомый ток всей цепи и искомые напряжения на н.с.1 и н.с.2.

Занятие 23 Контрольная работа №4 ЭТ У23

Контрольные вопросы:

1. 
   Дайте определения и назовите отличия между принципиальной схемой и схемой соединений.
   
2. 
   Что такое идеальный источник ЭДС?
   
3. 
   Что такое идеальный источник тока?
   
4. 
   Чем отличается расчетная электрическая схема от принципиальной электрической схемы?
   
5. 
   Что такое ветвь электрической цепи?
   
6. 
   Что представляет собой узел электрической цепи?
   
7. 
   Начертите схему с тремя контурами электрической цепи и дайте объяснения.
   
8. 
   Напишите формулу и дайте определение первому закону Кирхгофа.
   
9. 
   Напишите формулу и дайте определение второму закону Кирхгофа.
   
10. 
    Начертите схему с тремя контурами и составьте уравнения цепи по второму закону Кирхгофа.
    
11. 
    Начертите схему с последовательным соединением резисторов и напишите формулы для ее расчета
    
12. 
    Начертите схему с параллельным соединением резисторов и напишите формулы для ее расчета
    
13. 
    Начертите схему со смешанным соединением резисторов и напишите формулы для ее расчета
    
14. 
    Начертите схему электрической цепи и составьте потенциальную диаграмму для нее. Объясните порядок построения.
    
15. 
    Что такое нелинейные элементы электрических цепей?
    
16. 
    Начертите симметричную вольт-амперную характеристику нелинейного элемента и объясните ее сущность.
    
17. 
    Начертите несимметричную вольт-амперную характеристику нелинейного элемента и объясните ее сущность.
    
18. 
    Объясните сущность графического расчета нелинейных электрических цепей.
    

Тема 3 Магнитное поле. и магнитные цепи.

Занятие 24. Магниты и магнитное поле .

а) Постоянные магниты

В отличие от электромагнитов, приобретающих магнитные свойства лишь при включении тока, постоянные магниты имеют эти свойства изначально и сохраняют их неограниченно долго.

Проделаем опыт с дугообразным магнитом, Положим его в коробочку с мелкими железными опилками. Встряхнем коробочку и достанем магнит. Мы увидим, что опилки прилипают не ко всей поверхности магнита, а лишь к некоторым его частям – полюсам магнита. Любой магнит имеет не менее двух полюсов.

Рис.24.1. Опилки на полюсах магнита.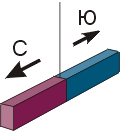



Рис.24.2. Ориентированный по сторонам горизонта магнит

Подвесимполосовой магнит на длинной нити так, чтобы он мог свободно поворачиваться. Когда качания магнита прекратятся, он обязательно расположится так, что один из его полюсов укажет в сторону северной части горизонта, а другой – в сторону южной. Поэтому полюсы магнита называются северным (N) и южным (S) полюсами.

Поднося к подвешенному магниту второй магнит, мы легко обнаружим, что их одноименные полюса отталкиваются, а разноименные – притягиваются. Этот опыт будет выглядеть эффектнее, если вместо тяжелых и неповоротливых полосовых магнитов использовать две легкие магнитные стрелки, свободно вращающиеся на остриях..

Рис. 24.3. Ориентированные относительно друг друга магнитные стрелки

б) Магнитное поле проводника с током: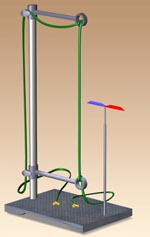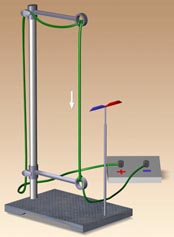



Рис.24.4. Тока в проводе нет Рис.24.5 Ток в проводе есть

В штативе закрепим провод, концы которого можно подключать к источнику тока. Рядом с проводом разместим магнитную стрелку от компаса, надетую на иглу.

Пока ток не включен, разместим приборы так, чтобы стрелка указывала на провод (рис.23.4)

При подключении концов провода к источнику постоянного тока стрелка "отвернется" от провода (рис.23.5).

Если магнитные стрелки отклоняются от первоначального направления, значит, в этих точках пространства действуют какие-то силы. Другими словами, в пространстве вокруг провода с током существует силовое поле. Это поле вокруг проводника с током называют магнитным полем.

Магнитное поле обнаруживается благодаря магнитным явлениям:

• 
  притяжению и отталкиванию проводов с токами или намагниченных тел,
  
• 
  действию проводника с током на магнитную стрелку,
  
• 
  электромагнитной индукции.
  

б) Магнитная индукция

Количественная оценка магнитной индукции:

Для оценки интенсивности магнитного поля введено понятие магнитной индукции. Магнитная индукция обозначается буквой В.

Магнитная индукция — векторная величина, характеризующая магнит­ное поле и определяющая силу, действующую на движущуюся заряженную частицу со стороны магнитного поля.

Модулем вектора магнитной индукции является отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока в проводнике на длину этого участка.:


Где: В - магнитная индукция " Тесла" [ Тл ]

I - сила тока в проводнике, А

∆l– длина участка проводника, м

Линии магнитной индукции

Графически магнитное поле можно изобразить с помощью линий магнитной индукции.

Магнитное поле тока прямолинейного провода имеет линии маг­нитной индукции в виде окружностей, лежащих в плоскостях, пер­пендикулярных направлению тока, с центром на оси

провода.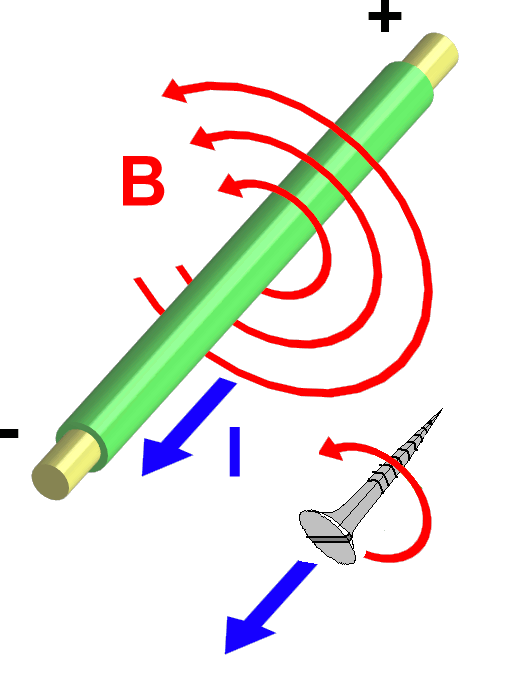


Направление магнитной индукции в этом случае определяется с помощью правила буравчика:

если направление поступательного движения буравчика (винта) совместить с направлением тока в проводе, то вращение рукоятки (головки винта) покажет направление линий магнитной индук­ции.

Рис. 24. 6. Линии магнитной индукции прямолинейного проводника с током

в) Напряженность магнитного поля

Для расчета магнитный полей применяют и другую физическую величину – напряженность магнитного поля Н . Единицей напряженности магнитного поля является Ампер/метр (А/м)

Связь между магнитной индукцией и напряженностью магнитного поля для немагнитных материалов определяется выражением



Где: В – магнитная индукция, Тл

Н – напряженность магнитного поля, А/м.

- магнитная постоянная

г) Магнитный поток

Величина магнитной индукции, проходящей через поверхность площадью s, перпендикулярной вектору магнитной индукции, называется магнитным потоком Ф.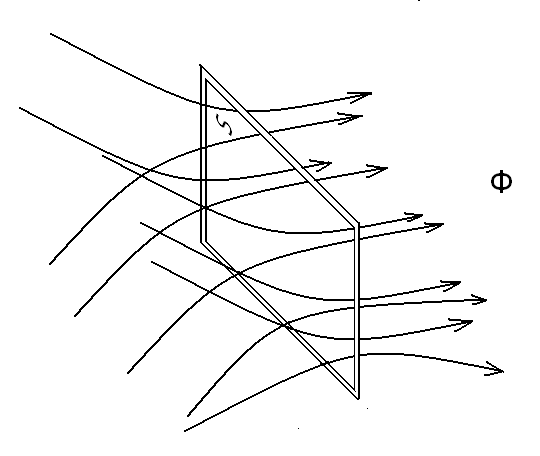



Рис.24.7. Магнитный поток

Величина магнитного потока определяется по формуле:

Ф=Вs

Где: Ф – магнитный поток Вб, вебер.

В- магнитная индукция, Тл

s – площадь площадки, м²


Занятие 25.Магнитные свойства веществ
а) Ферромагнетики, диамагнетики и пара­магнетики

Вещества, помещенные в магнитное поле, ведут себя по-раз­ному. Такие вещества, как золото, серебро, медь, цинк и ряд дру­гих, незначительно ослабляют магнитное поле внутри вещества. Их называют диамагнетиками.

Платина, магний, алюминий, хром, палладий, щелочные ме­таллы, кислород и др. наоборот незначительно увеличивают маг­нитное поле. Они называются парамагнетиками.

Вещества, в которых собственное (внутреннее) магнитное поле может в сотни и тысячи раз. превосходить вызвавшее его внешнее поле, называются ферромагнетиками. К ним относятся железо (Fe), кобальт (Со), никель (Ni), некоторые редкоземельные элементы, а также сплавы на базе этих элементов.

В электротехнике принято подразделять все вещества на маг­нитные (ферромагнетики) и немагнитные (диамагнетики и пара­магнетики).

Ферромагнетизм обусловлен наличием в веществе маленьких намагниченных областей — до­менов, в которых магнитные моменты атомов имеют одно и то же направление. Каждый домен является маленьким магнитом.

Ферромагнетик состоит из большого числа доменов, которые при отсутствии внешнего магнитного поля ориентированы про­извольным образом, так что ферромагнетик остается немагнит­ным.

При помещении ферромагнетика во внешнее магнитное поле домены, направление которых близко к направлению силовых линий внешнего поля, начинают расти, а домены, намагничен­ные против внешнего поля, уменьшаются и, наконец, исчезают.
При дальнейшем увеличении напряженности внешнего поля все домены устанавливаются вдоль силовых линий поля, наступает магнитное насыщение и намагниченность почти не растет.

Если теперь уменьшить напряженность внешнего поля до нуля, то ориентация доменов нарушится лишь частично, поэтому на­магниченность ферромагнетика уменьшается, но не до нуля.

Что­бы уничтожить остаточную намагниченность образца, нужно при­ложить внешнее поле противоположного направления. Напряженность такого магнитного поля называют коэрцитивной силой Н_с .

б) Магнитная индукция и напряженность магнитного поля ферромагнетиков
Для расчета индукции магнитного поля В в ферромагнетике используют выражение, которое учитывает способность к намаг­ничиванию материала,



где: Н — напряженность внешнего магнитного поля;

_r - относительная магнитная про­ницаемость материала;

_a - абсолютная магнитная проницаемость материала.

B – магнитная индукция

- магнитная постоянная

Для ферромагнетиков _r» 1, в то время как в немагнит­ных материалах _r = 1.
в) Характеристики магнитных материалов

Основными характеристиками ферромагнетиков являются кри­вая намагничивания В(Н) и петля гистерезиса (рис. 24.2)

Рассмотрим процесс переменного намагничивания маг­нитного материала.

Для этой цели намотаем на стальной сердеч­ник обмотку и будем по ней пропускать постоянный ток. Пред­положим, что сердечник электромагнита ранее не был намагни­чен.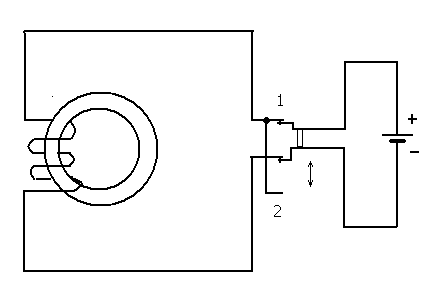



Рис.25.1. Схема опыта
Увеличивая проходящий по виткам обмотки ток I от нуля, мы тем самым будем увеличивать намагничивающую силу и напряженность поля Н.

Величина магнитной индукции Всердечнике бу­дет также увеличиваться.
Кривая намагничивания Оа имеет прямоли­нейную часть, а затем вследствие насыщения кривая поднимается медленно, при­ближаясь к горизонтали.
Если теперь, достигнув точки а , уменьшать Н, то будет уменьшаться и В. Однако уменьшение Впри уменьше­нии Н, т. е. при размагничивании, будет происходить с запазды­ванием по отношению к уменьшению Н. Величина остаточной индукции при Н=0 характеризуется отрезком Об.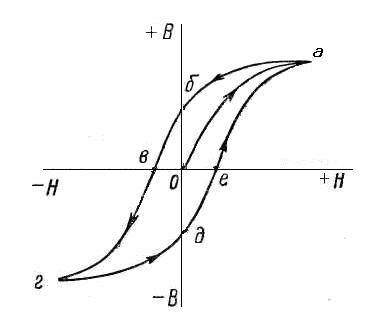


Рис.25.2. Петля гистерезиса.


Для того чтобы магнитная индукция в сердечнике стала рав­ной нулю, необходимо намагничивать материал в обратном на­правлении, т. т.е. перемагничивать его.

Для этой цели направление тока в обмотке меняется на обратное. Направление магнитных линий и напряженности поля также изменяется. При напряжен­ности поля Н=ов,индукция в сердечнике равна нулю и мате­риал сердечника полностью размагничен.

Значение напряжен­ности поля Н = овпри В = 0 является определенной характери­стикой материала и называется задерживающей (коэрцитивной) силой.

Повторяя процесс перемагничивания, мы получаем замкну­тую кривую а б в г д е а, называемую петлей гистерезиса.

На этом опыте легко убедиться, что намагничивание и размагничи­вание сердечника (появление и исчезновение полюсов, магнитной индукции или магнитного потока) отстают от момента появле­ния и исчезновения намагничивающей и размагничивающей силы (тока в обмотке электромагнита

Если величина напряженности магнитного поля превышает значение, при котором наступает магнитное насыщение, т. е. Н_max > H_S, то размеры петли больше не увеличиваются, растут только безгистерезисные участки (а и г см. на рис. 24.2.) Такая петля назы­вается предельной петлей гистерезиса.

Намагничивание ферромагнитного материала, впервые поме­щенного в магнитное поле, происходит по линии оа. Точки в и е предельной петли гистерезиса соответствуют коэрцитивной силе Н_с(-Н_с), а точки б и д дают значения остаточной индукции В_г(-В_г).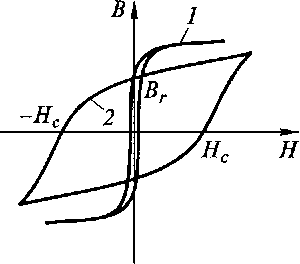



Рис.25.3. Петли гистерезиса магнитомягких и магнитотвердых материалов

В зависимости от значения коэрци­тивной силы все магнитные материалы принято делить на магнитомягкие (кривая 1 рис.24.3;) и магнитотвердые (кривая-2).

Магнитомягкие материалы имеют малую коэрцитивную силу и узкую петлю гистерезиса. К этой группе относят электротехническую сталь, пермаллои, ферриты. Приме­няют эти материалы в таких электротехнических устройствах, как электрические машины, трансформаторы, электрические аппа­раты и др.

Магнитотвердые материалы имеют большую коэрцитивную силу и широкую петлю гистерезиса. Будучи намагниченными, они со­храняют намагниченность и после снятия намагничивающего поля. Из таких материалов изготовляют постоянные магниты, которые широко применяются в различных устройствах.
У26. Классификация, элементы и характеристики магнитных цепей

Для электрических машин и многих электротехнических уст­ройств основным функциональным элементом является магнит­ная система. Обычно магнитную систему представляют в виде маг­нитной цепи.

Магнитная цепь содержит источники магнитного поля, систе­му магнитопроводов из ферромагнитного материала, другие ве­щества или воздушный зазор, по которым замыкается магнитный поток (рис. 25.1).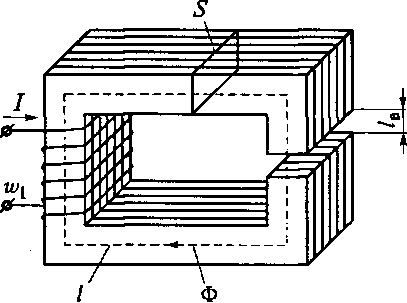

Рис.26.1. Неразветвленная магнитная цепь

В качестве источника магнитного поля обычно применяется катушка с числом витков w₁,по которой протекает ток I.

Обмотка с током возбуждает магнитное поле и характеризуется магнито­движущей силой (МДС)



Где: F – магнитодвижущая сила, А

I - сила тока, А

w – количество витков катушки.
Единицей МДС является ампер (А), еще эту единицу называют ампер-виток.

В магнитной цепи МДС играет такую же роль, как ЭДС в электрической.


Проводя аналогию с электрической цепью, отметим, что в магнитной цепи магнитопровод играет роль проводов, а роль на­грузки играет, как правило, воздушный зазор, в котором для функ­ционирования устройства необходимо создать определенное магнитное поле.

Магнитная цепь может быть неразветвленной (см. рис. 25.1)и разветвленной (см. рис. 25.2).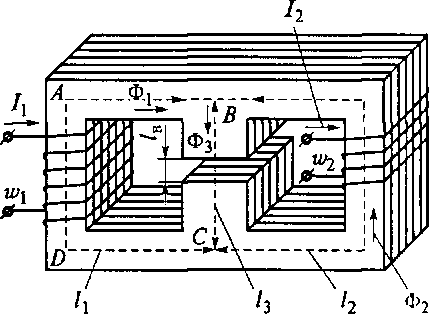


Рис.26.2. Разветвленная магнитная цепь
Реальная магнитная цепь характеризуется не только магнитным потоком Ф, протека­ющим по магнитопроводу, но и потоками рассеяния Ф„ а также выпучиванием магнитных силовых линий в области воздушного зазора.

Обычно при анализе магнитных цепей пользуются следую­щими допущениями: индукция В принимается постоянной по се­чению; пренебрегают потоками рассеяния и выпучиванием; вво­дят среднюю длину различных участков магнитопровода.

Занятие 27. Основные законы магнитной цепи.

Расчет простейших магнитных цепей
а) Законы Кирхгофа для магнитных цепей.
Расчет магнитных цепей проводится на основе законов Кирх­гофа для магнитных цепей. Этих законов два.

Первый закон Кирхгофа

Применяют к магнитным узлам разветвленной магнит­ной цепи. Согласно этому закону алгебраическая сумма потоков равна нулю.

Для цепи (см. рис. 26.2)имеем


Второй закон Кирхгофа

Применяют к магнитным контурам. В соответствие с этим законом алгебраиче­ская сумма магнитных напряжений равна алгебраической сумме намагничивающих сил в контуре.

Для контура АВСD (см. рис.26.1) получаем

или
Где: - магнитные напряжения на различных участках магнитной цепи

Единицей магнитного напряжения является Ампер (А)


Рис.27.1. ко второму закону Кирхгофа
Часто при расчете магнитных цепей применяют закон Ома для участка магнитной цепи. По аналогии с электрической цепью маг­нитное сопротивление выражается отношением


Магнитное сопротивление магнитопровода цепи, изображен­ной на рис.26.2. равно:

Рис.27.2. к расчету магнитного сопротивления цепи

Магнитное сопротивление воздушного зазора R_м.в.той же цепи равно.

Где: - магнитные напряжения магнитопровода и воздушного зазора соответственно;

S — площадь магнитного сер­дечника.
б) Примеры расчета магнитной цепи.

При расчете неразветвленной магнитной цепи различают две задачи: прямую и обратную.
В прямой задаче известны геометрические размеры, магнитные свойства магнитопровода и значение маг­нитной индукции В или магнитного потока Ф.
В обратной задаче по заданному значению МДС обмотки расчета магнитной цепи определяется магнитный поток или индукции. Причем задача решается методом последовательных приближений, когда произвольно задаются значением искомого магнитного потока и решают прямую задачу, находя соответствующую МДС. Если она не соответствует заданной, изменяют значение потока и снова решают прямую задачу. Процесс повторяют до получения удовлетворительного совпадения расчетной МДС с заданной.
Пример 1:

Рассмотрим прямую задачу для магнитной цепи (см. рис.26.2).

Последовательность решения:

• 
  По закону полного тока
  

Где:

• 
  Поток связан с индукцией соотношением Ф = BS, поэтому при заданном потоке находим индукцию В.
  
• 
  Затем по кривой намагничивания В(Н) находим Н,
  
• 
  затем находим Iw.
  

Задача:

Определить количество витков обмотки электромагнита (рис.26.3.) ,

если ток электромагнита I=20А,

а поток, при котором якорь начинает притягиваться равен Ф=30∙10^-4 Вб.

Магнитопровод изготовлен из электротехнической стали ЭЗЗО.

Размеры электромагнита: l₁= 30 см; l₂=5 см; l₃ = l₄ = 12 см; l_в = 0,5 см; S₁ = 30 см²; S₃= 25 см².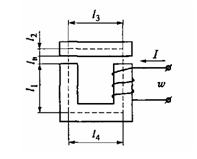


Рис.27.3. Магнитная цепь электромагнита

Решение:

1. 
   Определим магнитную индукцию на участках магнитопровода:
   

2) По кривой намагничивания для стали Э330 ( см. рис.26.4) определяем напряженность магнитного поля Н₁ и Н₃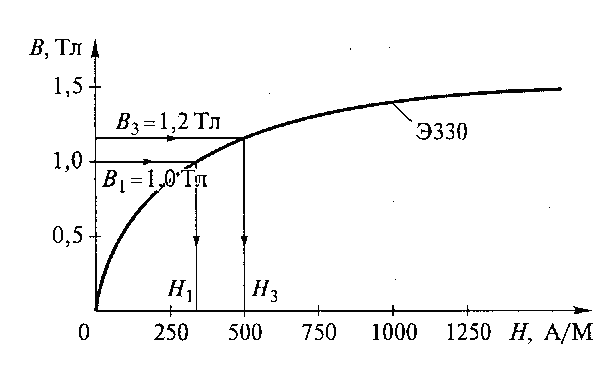






Рис.27.4. Кривая намагничивания стали Э330
Напряженность в воздушном зазоре Н_в = 8 ∙ 10⁵В₁= 8∙10⁵ А/м.
Магнитодвижущая сила
Iw = Н₁(2l₁ +l₄) + H_в∙2l_в + H₃(2l₂ + l₃) = 312,5 ∙ (2 ∙30 + 12) ∙ 10 ^-2 + 8∙10⁵∙2∙ 0,5 ∙10 ^-2 +

+500(2∙2,25 + 12) ∙10 ^-2 = 8310 А.
Число витков
Занятие 28 Сила Ампера

а) Опыт по определению силы Ампера

Выясним, как поле магнита будет действовать на проводник с током. (см.рис.27.1 и 27.2.)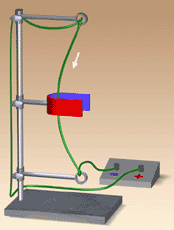



Рис.28.1. В проводнике тока нет. Рис.28.2. По проводнику протекает ток
В начале опыта провод свисает свободно, извиваясь при этом (рис.1). Если же концы провода присоединить к источнику постоянного тока, то провод втягивается внутрь магнита (рис.2).

Переменив подключение концов провода к "+" и "–" источника тока, мы обнаружим, что провод выталкивается из промежутка между полюсами магнита.

Видоизменим опыт. Вместо проводника в виде гибкого провода возьмем толстую алюминиевую проволоку, согнутую в виде жесткой рамки..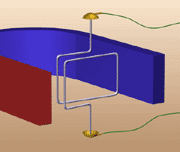

Рис.28.3 Тока в рамке нет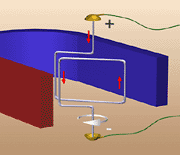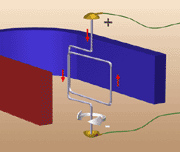

Рис.28.4 и 28.5. Ток в рамке есть, рамка поворачивается на 90 градусов
Если сначала рамка расположена так, как на рисунке 27. 3, то после включения тока (рис.27.4) рамка начнет поворачиваться, пока не займет положение, показанное на рисунке 27.5.

Выясним теперь, почему рамка вообще поворачивается. На рисунке 27. 4 показано, что в левой части рамки ток идет вниз (и эта часть перемещается в глубь магнита), а в правой части рамки ток идет вверх (и она перемещается наружу).

Итак, на противоположные стороны рамки с током, находящейся в магнитном поле, действуют противоположно направленные силы, разворачивающие рамку.

Сила, действующая на проводник с током , находящемся в поле постоянного магнита называется электромагнитной силой или силой Ампера.
На рисунке 28.6 показан прямолинейный провод в пространстве между по­люсами постоянного магнита, расположенный так, что между направлениями вектора магнитной индукции В и тока в проводе I угол α = 90°.
На проводник с током в магнитном поле действует сила Ампера, величина которой определяется формулой:

F=B·I·l sin α

где: В — магнитная индукция, Тл;

I —ток в проводе, А;

l —длина части провода, расположенной в маг­нитном поле, м;

F— величина элек­тромагнитной силы, Н.
На провод с током, расположен­ным вдоль линий магнитной индукции, магнитное поле не действует.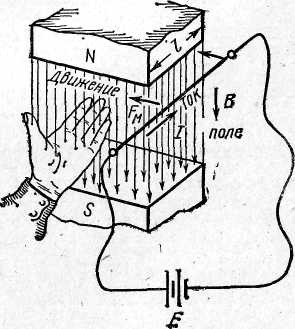

Рис. 28. 6. Определение направления действия силы Ампера.
Направление электромагнитной силы наиболее определяется по правилу левой руки.
Правило левой руки :
Если расположить левую руку так, чтобы вытянутые четыре пальца (кроме большого) показывали направление тока в проводе, а линии магнитной индукции «входили» в ладонь, то большой палец, отогнутый перпендикулярно остальным четырем, покажет направле­ние электромагнитной силы.
Занятие 29 Электромагнитная индукция.
а) Явление электромагнитной индукции:
Если проводник без тока перемещать в поле постоянного магнита, то на концах проводника возникает электродвижущая сила. То есть проводник становится источником электрической энергии. Это явление называется явлением электромагнитной индукции.
Индуктированная э. д. с. возникает в следующих трех слу­чаях:

• 
  Когда движущийся проводник пересекает неподвижное магнитное поле или, наоборот, перемещающееся магнитное поле пересекает неподвижный проводник; или когда проводник и магнитное поле, двигаясь в пространстве, перемещаются один отно­сительно другого.
  
• 
  Когда .переменное магнитное поле одного проводника, дей­ствуя на другой проводник, индуктирует в нем э. д. с. (взаимо­индукция).
  
• 
  Когда изменяющееся магнитное поле проводника индукти­рует в нем самом ЭДС,
  

(самоиндукция).
Таким образом, всякое изменение во времени величины маг­нитного потока, пронизывающего замкнутый проводящий контур (виток, рамку), сопро­вождается появлением в проводнике . индуктиро­ванной ЭДС.
б) Определение величины и направления индуктированной эдс: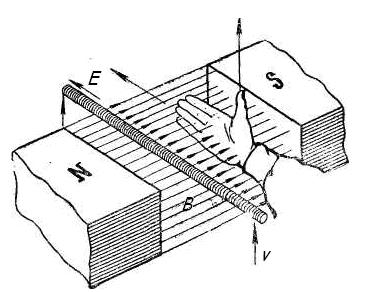


Рис.29.1. Определение направления ЭДС в движущемся проводнике
Направление индукти­рованной ЭДС зависит от направления движения проводника и от направ­ления магнитного поля.

Для определения на­правления индуктирован­ной ЭДС в проводнике служит
правило правой руки:
Если мыс­ленно расположить пра­вую руку в магнитном поле вдоль проводника так, чтобы магнитные ли­нии, выходящие из северного полюса, входили в ладонь, а боль­шой отогнутый палец совпадал с направлением движения про­водника, то четыре вытянутых пальца будут показывать направ­ление индуктированной ЭДС в проводнике (см. рис.28. 1.).
Величина индуктированной ЭДС находится по формуле:


Где: е – индуктированная эдс, В.

В – магнитная индукция магнита, Тл.

l– длина проводника, м.

v – скорость движения проводника, м/с.

α – угол между магнитными линиями и проводником, °.

Занятие 30 Самоиндукция
а) Явление самоиндукции.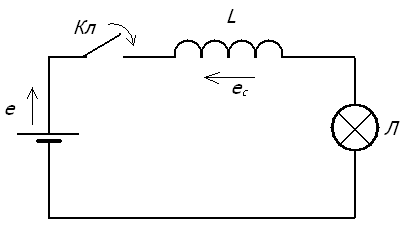


Рис.30.1. Схема опыта.


При замыкании выключателя Кл в цепи с катушкой и лампочкой возникнет электрический ток , однако лампочка загорается не сразу после замыкания контактов выключателя. Это запаздывание загорания лампочки объясняется явлением самоиндукции при протекании электрического тока по виткам катушки.

С появлением тока вокруг проводника возникает маг­нитное поле, индукционные линии которого пересекают витки катушки и индуктируют в них ЭДС.

Эта ЭДС называется ЭДС самоиндукции.

Так как всякая индуктированная ЭДС направлена против причи­ны, ее вызвавшей, а этой причиной будет ЭДС источника, то ЭДС самоиндукции будет направлена против ЭДС источника.

Таким образом, ток устанавливается в цепи не сразу. Толь­ко когда магнитный поток установится, пересечение проводни­ка магнитными линиями прекратится и ЭДС самоиндукции ис­чезнет. Тогда в цепи будет протекать постоянный ток.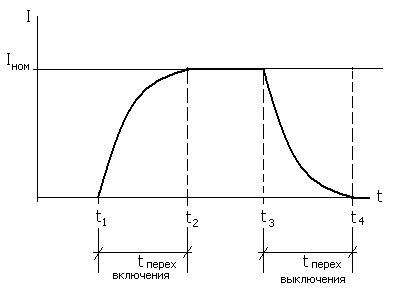



Рис. 30.2. График нарастания тока в цепи с учетом э. д. с. самоиндукции


б) Индуктивность цепи.
При размыкании цепей, содержащих большое количество витков и массивные стальные сердечники или, как говорят, об­ладающих большой индуктивностью, ЭДС самоиндукции мо­жет быть во много раз больше ЭДС источника напряжения.

Следует учитывать, что ЭДС самоиндукции проявляет себя не только в моменты включения и выключения цепи, но также и при всяких изменениях тока.

Величина ЭДС самоиндукции зависит от скорости измене­ния тока в цепи и определяется выражением :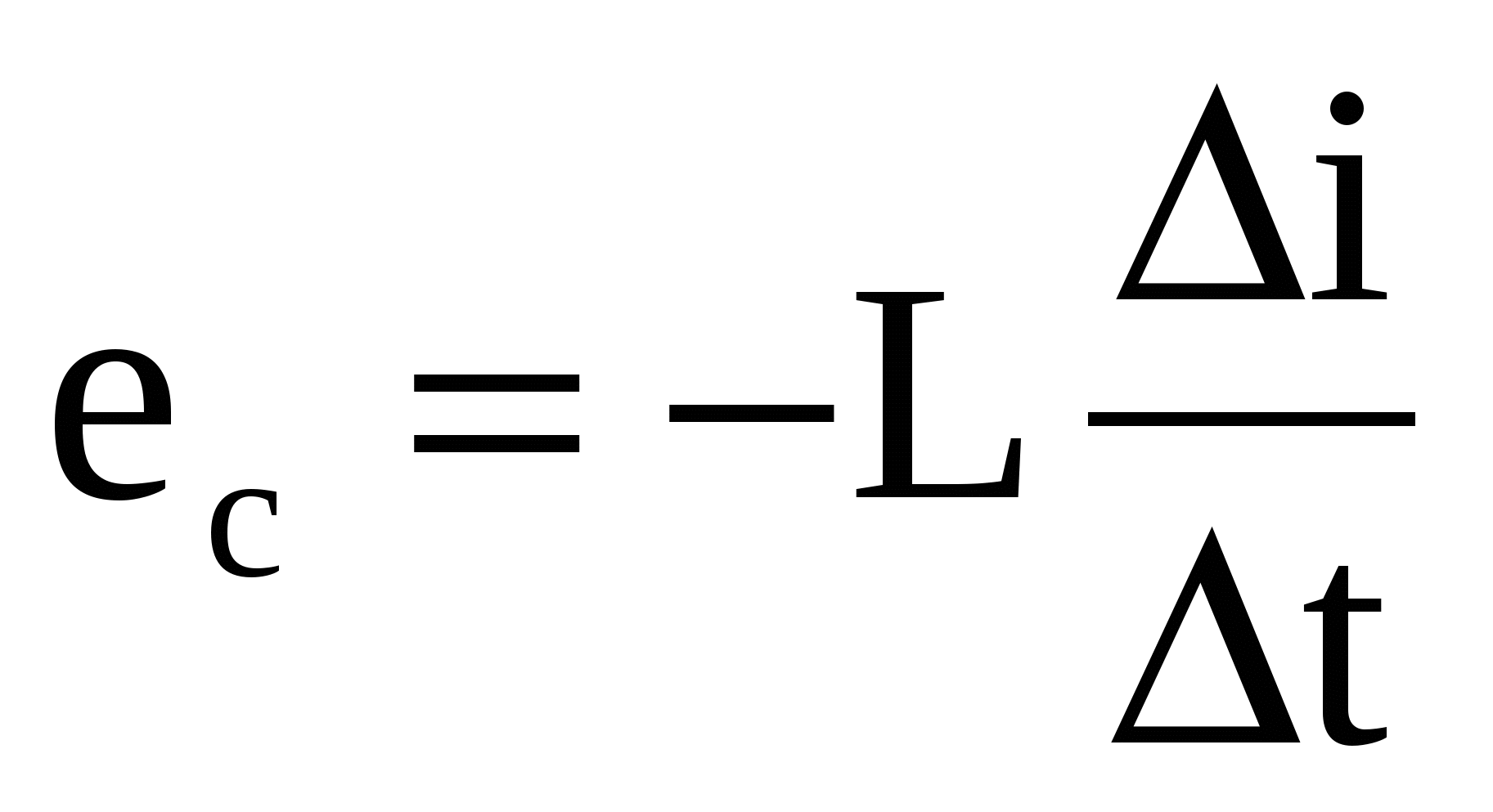

Где: – скорость изменения тока в цепи, А/с.

L – коэффициент пропорциональности, называемый индуктивностью, Гн (генри)
1 генри = 10³ миллигенри (мГн) = 10⁶ микрогенри (мкГн).
Знак "-" говорит о том, что эдс самоиндукции всегда направлена встречно эдс источника основного тока.
Величина ЭДС самоиндук­ции зависит от индуктив­ности самой цепи. Цепями с боль­шой индуктивностью являются обмотки генераторов, электродви­гателей, трансформаторов и ин­дукционных катушек, обладаю­щих стальными сердечниками.
Меньшей индуктивностью обла­дают прямолинейные провод­ники. Короткие прямолинейные проводники, лампы накаливания и электронагревательные приборы (печи, плитки) индуктивностью практически не обладают и появления ЭДС самоиндук­ции в них почти не наблюдается.

Занятие 31 Взаимоиндукция
а) Явление взаимоиндукции.




Рис.31.1. Магнитосвязанные катушки
Если по одной из двух магнитносвязанных катушек (см. рис.29.1.) пропустить переменный ток, то на концах обмотки второй катушки появится электродвижущая сила.

Это явление называется взаимоиндукцией.

Величина эдс взаимоиндукции зависит от параметров обеих катушек, а также от параметров магнитной среды между катушками.

Эта магнитная взаимосвязь выражается коэффициентом магнитной взаимосвязи М.

Предположим, что изменяется токi₁в первой катушке. ЭДС взаимоиндукции е₂ во второй катушке пропорциональна скорости изменения этого тока: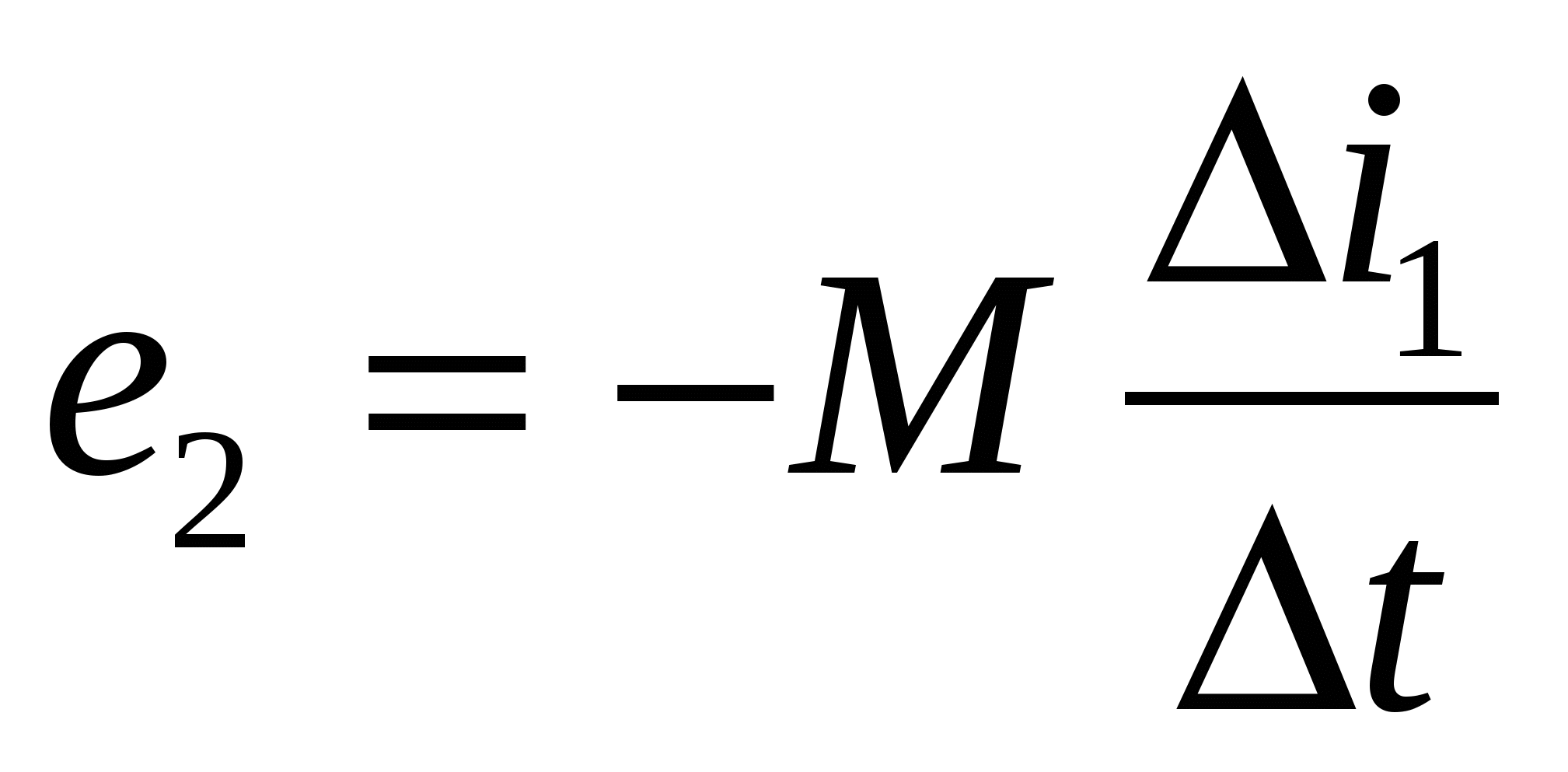


Аналогично, при изменении токаi₂ЭДС взаимоиндукции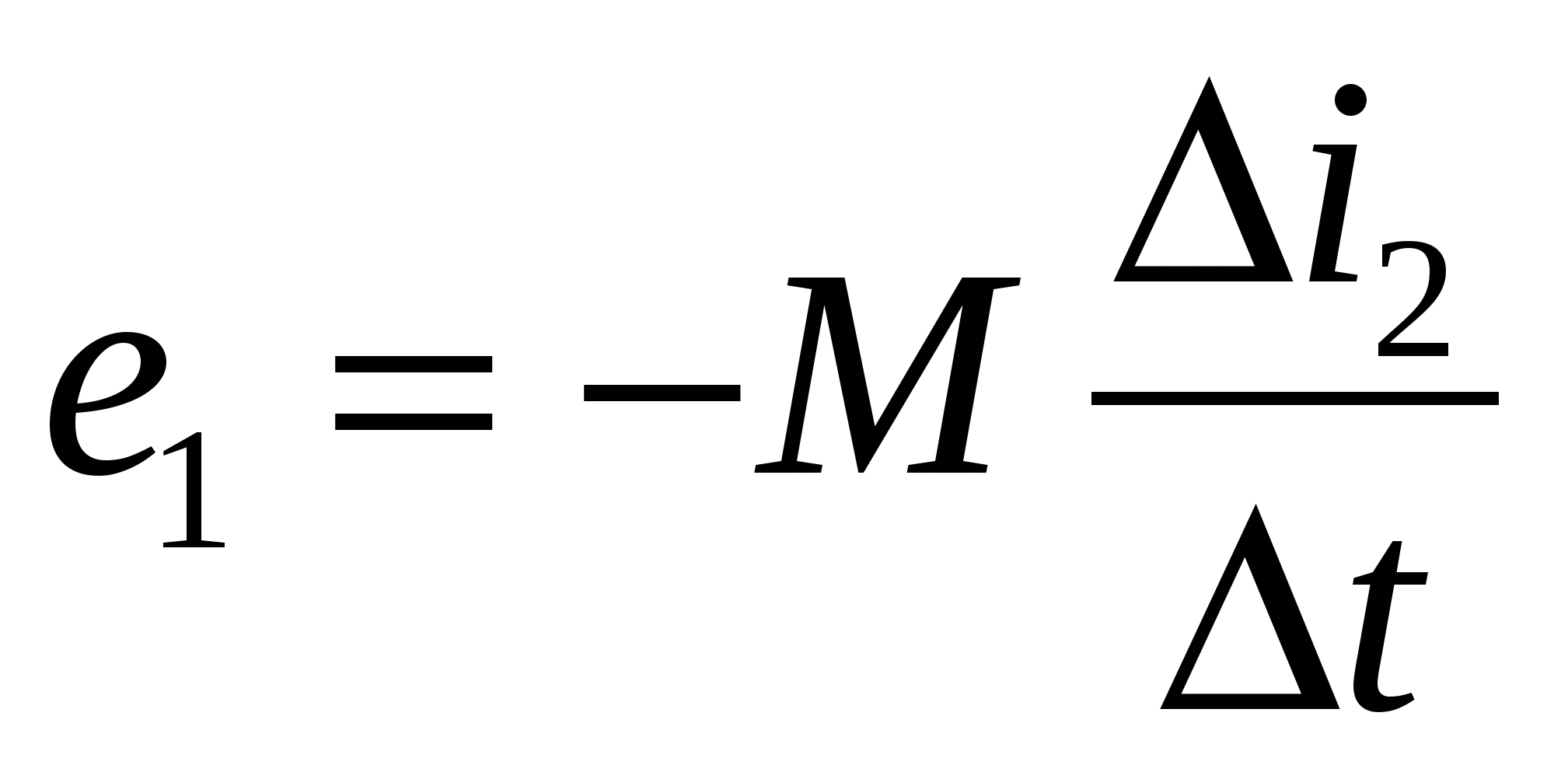


В том и другом случае коэффициентом пропорциональности является взаимоиндуктивность системы М.
Знак "-" в применении к такой системе указывает на то, что изменение тока в одной катушка встречает противодействие со стороны другой катушки.

Занятие 32 Контрольная работа ЭТ У32

Контрольные вопросы:

1. 
   Назовите способы определения магнитного поля проводника с током.
   
2. 
   Дайте определение и напишите формулу магнитной индукции.
   
3. 
   Опишите правило и приведите чертеж для направления магнитной индукции проводника с током
   
4. 
   Дайте определение напряженности магнитного поля.
   
5. 
   Дайте определение и напишите формулу магнитного потока.
   
6. 
   Дайте определение ферромагнетикам и диамагнетикам.
   
7. 
   Приведите формулу для определения магнитной индукции ферромагнетиков.
   
8. 
   Что является характеристиками магнитных материалов?
   
9. 
   Опишите опыт получения петли Гистерезиса?
   
10. 
    Чем отличаются друг от друга магнитомягкие и магнитотвердые материалы?
    
11. 
    Начертите петлю гистерезиса магнитотвердого материала и укажите на ней величину остаточной магнитной индукции.
    
12. 
    Начертите петлю гистерезиса магнитотвердого материала и укажите на ней величину коэрцитивной силы.
    
13. 
    Приведите и объясните формулу для определения магнитодвижущей силы.
    
14. 
    Напишите и объясните формулу первого закона Кирхгофа для расчета магнитных цепей.
    
15. 
    Напишите и объясните формулу второго закона Кирхгофа для расчета магнитных цепей.
    
16. 
    Напишите и объясните формулы для определения магнитного сопротивления участка магнитопровода.
    
17. 
    Что такое кривая намагничивания и для каких целей она используется?
    
18. 
    Дайте определение и напишите формулу силы Ампера.
    
19. 
    Приведите рисунок и правило для определения направления действия силы Ампера.
    
20. 
    Опишите явление электромагнитной индукции.
    
21. 
    Напишите формулу для определения величины ЭДС электромагнитной индукции.
    
22. 
    Приведите рисунок и правило для определения направления действия ЭДС электромагнитной индукции.
    
23. 
    Опишите явление самоиндукции.
    
24. 
    Дайте определение и объясните понятие индуктивности цепи.
    
25. 
    Опишите явление взаимоиндукции.
    
26. 
    Напишите формулу для определения ЭДС самоиндукции и объясните ее.
    

Примечание: Каждому учащемуся необходимо решить задачу, предложенную преподавателем.