Программа по дисциплине Теоретические основы электротехники
 Скачать 5.49 Mb. Скачать 5.49 Mb.
|
|
Тема 4. Электрические цепи переменного тока Занятие 33. Переменная ЭДС. а) Вращение витка в равномерном магнитном поле ЭДС в рамке, имеющей два активных проводника длинойl (см. рис.32.1) ,при ее вращении в поле постоянного магнита возникает ЭДС, равная е = 2B·v·l· sin β (в дальнейшем все изменяющиеся во времени величины: токи, напряжения, ЭДС и т. д.—будем обозначать малыми буквами в отличие от постоянных значений для тех же величин, которые обозначают большими буквами). При равномерном вращении рамки линейная скорость проводника не изменяется и будет равна: Где: D – диаметр рамки.(м) ω – угловая скорость вращения рамки, ( градус/с) 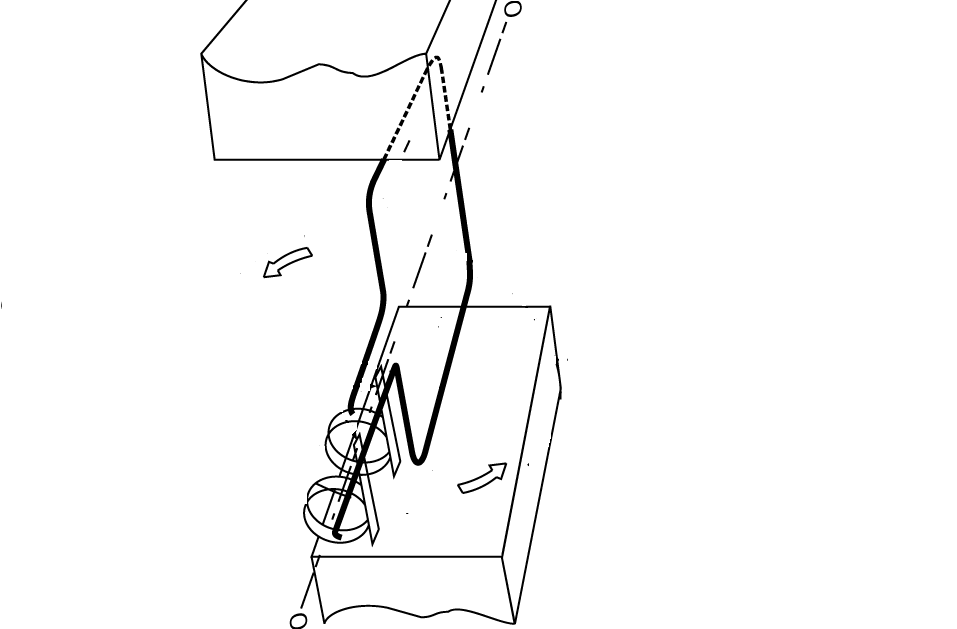 Рис.33.1. Генератор для получения переменного тока. Угол между направлением скорости и направлением магнитного поля изменяется пропорционально времени: Угол β определяет положение вращающейся рамки относительна плоскости, перпендикулярной направлению магнитной индукции. (см.рис.32.2) Положение рамки в момент начала отсчета времени t = 0 характеризуется углом β = 0. Поэтому ЭДС в рамке является синусоидальной функцией времени : е = BlDωsinωt. Наибольшей величины ЭДС достигает при угле β= ωt = 90° Еm = BlDω; тогда мгновенное значение ЭДС при любом угле поворота рамки β определится выражением: е = Em sin ωt. В рассмотренном случае синусоидальное изменение ЭДС достигается за счет непрерывного изменения угла, под которым проводники пересекают линии магнитной индукции. 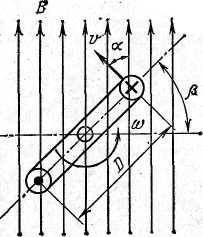 Рис.33.2. Вращение рамки в магнитном поле График, полученной при вращении витка в поле постоянного магнита, переменной ЭДС показан на рисунке 32.3. Положения 1 и 3 соответствуют угу поворота β=0 и β=180°, положения 2 и 4 соответствуют углу поворота β=90° и β=270°. 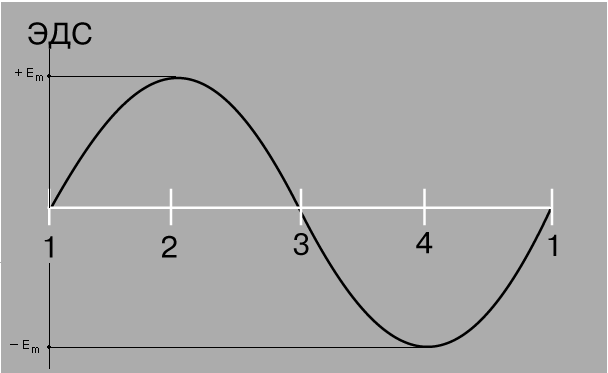 Рис.33.3. График переменной ЭДС Занятие 34 Параметры переменного тока а) Уравнение и график синусоидально изменяющихся величин Уравнение любой синусоидально изменяющейся величины имеет вид: e=Em sin (ωt +ψ) График синусоидально изменяющейся величины приведен на рисунке 33. 1. Уравнением и графиком задаются все характеристики синусоидально изменяющейся величины:
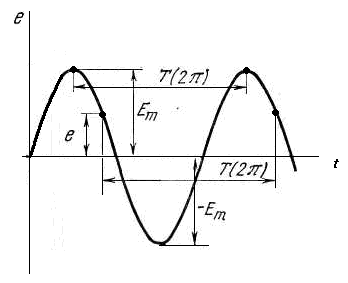 Рис.34.1. График синусоидально изменяющейся величины. б) Параметры переменной величины. Приведенные ниже определения распространяются на все величины, изменяющиеся по синусоидальному закону (ЭДС, ток, напряжение и др.). Для краткости изложения излагаем определения только для электродвижущей силы.
Начальная фаза ψ —фаза синусоидальной ЭДС в начальный момент времени. Если синусойда начинается с нулевого положения, то начальная фаза равна нулю. (см. рис.1) Синусойда тока (см. рис.33.2 ) опережает синусойду напряжения на угол 90° (π/2), следовательно начальная фаза тока будет равна π/2. Уравнения для напряжения и тока будут выглядеть: u=Um sin ωt i=Im sin (ωt + π/2)
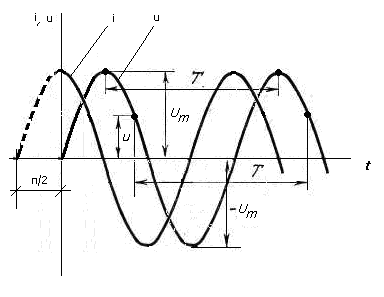 Рис.34.2. Графики тока и напряжения, сдвинутых по фазе на π/2 в) Действующая величина переменного тока При определении действующей величины переменного тока можно исходить из какого-либо его действия в электрической цепи (теплового, механического взаимодействия проводов с токами и т. д. ). Будем исходить из теплового действия тока. 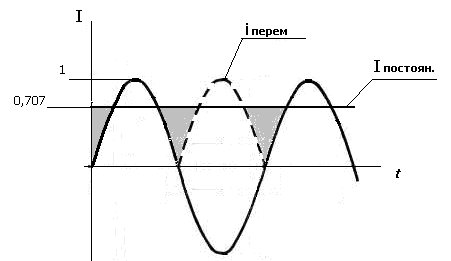 Рис. 34.3. Тепловое действие переменного и постоянного тока. Если за один и тот же промежуток времени измерить количество тепла, выделенное на активном элементе электрической цепи, постоянным и переменным током, то окажется, что постоянный ток выделит тепла больше, чем переменный. Чтобы постоянный и переменный ток выделили одинаковое количество тепла, необходимо уменьшить амплитуду постоянного тока. Рассчитано, что при выполнении этого условия амплитуда постоянного тока будет составлять 0,707 от амплитуды переменного тока. Действующая величина переменного тока I численно равна величине постоянного тока, который в одном и том же элементе цепи за время периода Т выделяет столько же тепла, сколько при тех же условиях выделяет переменный ток. Расчеты показывают, что I = 0,707 Im Аналогично: U = 0,707 Um E = 0,707 Em Где: I, U, E – действующие значения тока, напряжения и ЭДС. Im, Um, Em – амплитуда тока, напряжения и ЭДС Занятие 35 Сложение и вычитание синусоидальных величин. а) Сложение синусоидальных величин, выраженных в виде графиков На рисунке 35.1.показаны две синусоидальных величины (графики 1 и 2) . Для того, чтобы получить суммарный график (график 3) необходимо сложить значения ординат в одноименных временных значениях графиков 1 и 2. 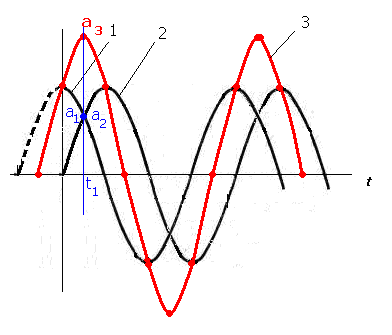 Рис.35.1. Графическое сложение синусоидальных величин Например, для получения ординаты точки а3 в момент времени t 1 суммировали ординаты точек а1 и а2 в этот же момент времени. Аналогично получают и график разности синусоидальных величин. Этот способ неудобен и применяется редко. Для проведения математических операций с синусоидальными величинами их представляют в виде векторов. б) Изображения синусоидальных величин в векторной форме Известно, что проекция отрезка, вращающегося вокруг оси с постоянной угловой скоростью, на любую линию, проведенную в плоскости вращения, изменяется по синусоидальному закону. Пусть отрезок прямой длиной Im начинает вращаться вокруг оси 0 из положения, когда он образует с горизонтальной осью угол φ, и вращается против часовой стрелки с постоянной угловой скоростью ω. Проекция отрезка на вертикальную ось в начальный момент времени . Когда отрезок повернется на угол α1, проекция его . Откладывая углы α1, α2, ... на горизонтальной оси, а проекции отрезка прямой - на вертикальной оси, получим ряд точек синусоиды (рис. 35.2). 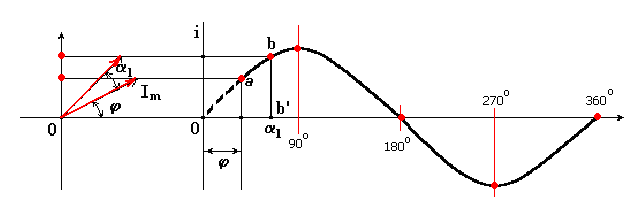 Рис.35.2. Представление синусоидальной величины в векторной форме Пусть даны два синусоидальных тока: . Нужно сложить эти токи и получить результирующий ток: 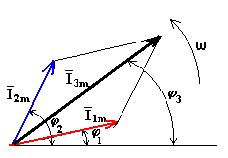 Рис.35.3.Сложение векторов двух величин Представим синусоидальные токи i1 и i2 в виде двух радиус - векторов, длина которых равна в соответствующем масштабе I1m и I2m. Эти векторы расположены в начальный момент времени под углами φ1 и φ2 относительно горизонтальной оси. Сложим геометрически отрезки I1m и I2m. Получим отрезок, длина которого равна амплитудному значению результирующего тока I3m. Отрезок расположен под углом φ3 относительно горизонтальной оси. Все три отрезка вращаются вокруг оси 0 с постоянной угловой скоростью ω. Проекции отрезков на вертикальную ось изменяются по синусоидальному закону. Будучи остановленными для рассмотрения, данные отрезки образуют векторную диаграмму (рис. 35.3). Занятие 36 Векторная диаграмма. Векторная диаграмма - это совокупность векторов, изображающих синусоидальные напряжения, токи и ЭДС одинаковой частоты. а) Представление синусоидальных величин неподвижными векторами. «Остановим» вращение векторов, представляющих токи и напряжения в момент t = 0.Тогда мгновенному значению синусоиды i (0) =Im sin φ соответствует вектор длиной Im, повернутый на угол φ от горизонтали против часовой стрелки . Этот вектор представляет или отображает синусоиду i(t)_ = Imsin (ωt+φ), т. е. дает информацию о ее двух отличительных параметрах: амплитуде Im и начальной фазе -φ. 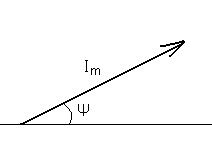 i (0) =Im sin φ Рис.36.1. Представление синусоидальной величины с помощью неподвижного вектора б) Сложение векторных величин. Представление синусоидальных величин неподвижными векторами значительно упрощает операции сложения и вычитания синусоидальных токов и напряжений. Как известно из курса математики, сложение векторов на плоскости выполняется по правилу параллелограмма (см.рис.36.2): результирующий вектор есть диагональ параллелограмма, сторонами которого являются слагаемые векторы. В целях упрощения рисунка сложение рекомендуется проводить другим способом: путем переноса второго слагаемого вектора параллельно самому себе так, чтобы его начало совпало с концом первого слагаемого вектора. Тогда вектор, равный сумме двух векторов, Ī рез = Ī m1 + Ī m2 проводится из начала первого вектора в конец второго. Этот способ суммирования предусматривает меньшее число построений и не затемняет чертеж параллельными сторонами параллелограмма. Поэтому в дальнейшем будет использоваться преимущественно именно этот способ: последовательное построение векторов так, чтобы начало второго вектора совпадало с концом первого и т. д. Графическое сложение векторов значительно проще и наглядней, чем операции с мгновенными токами .  Рис.36.2 Сложение векторов. Занятие 37 Контрольная работа ЭТ У37 Контрольные вопросы:
Тема 5. Элементы и параметры цепей переменного тока (22 часа) Занятие 38 . Активное сопротивление в цепи переменного тока. Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R.  Рис.38.1. а) цепь с активным сопротивлением. б) графики тока и напряжения. в) векторные диаграммы Для схемы, изображенной на рис38.1, заданы сопротивление Rи напряжение, изменяющееся по закону u = Umsin ωt. Требуется определить ток I в цепи. Выражение для мгновенного тока найдем по закону Ома: где Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением Rсовпадают по фазе. Это показано на графиках и векторной диаграмме (см.рис.38. 1 б,в.). Активное сопротивление не реагирует на изменение частоты тока в цепи. Занятие 39 Цепь переменного тока с индуктивностью: а) Индуктивное сопротивление Катушка из тонкого провода, намотанная на сердечник (или без сердечника), включенная в цепь переменного тока, обладает индуктивным сопротивлением. Величина индуктивного сопротивления определяется выражением: ХL = ωL = 2π∙f L Где: ХL – индуктивное сопротивление, Ом. ω – циклическая частота, рад/с L– индуктивность катушки, Гн "генри" f – частота тока в цепи, Гц. Из формулы видно, что при повышении частоты тока индуктивное сопротивление увеличивается, а при снижении частоты тока – уменьшается. То есть индуктивное сопротивление реагирует на частоту тока в цепи, поэтому его еще называют реактивным. Для постоянного тока f=0, поэтому для постоянного тока катушка не имеет индуктивного сопротивления. Индуктивность катушки L зависит от конструкции катушки (числа витков, наличия сердечника и его материала, конфигурации катушки и других факторов) Цепь, содержащая индуктивность, является искусственной, так как реальная катушка кроме индуктивности L содержит активное сопротивление R. Но мы рассмотрим идеальную катушку, в которой активное сопротивление R=0. В отдельных случаях активным сопротивлением реальной катушки можно пренебречь из-за его малости. б) Ток и напряжение в цепи переменного тока с катушкой индуктивности. 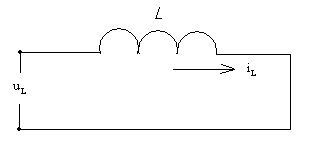 а) Схема цепи с индуктивностью 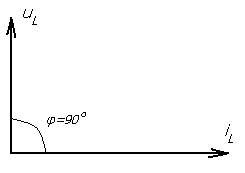 б) Векторная диаграмма цепи с индуктивностью. 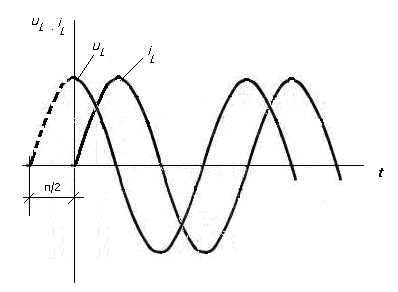 в) Графики тока и напряжения в цепи с индуктивностью Рис.39. 1. Электрическая цепь с индуктивностью. При прохождении синусоидального тока напряжение на катушке будет равно то есть напряжение на индуктивности опережает ток по фазе на угол 90° (π /2). Занятие 40 . Цепь переменного тока с емкостью а) Емкостное сопротивление Две металлических пластины, разделенные диэлектриком, называются электрическим конденсатором и обладают емкостным сопротивлением Величина емкостного сопротивления определяется выражением: 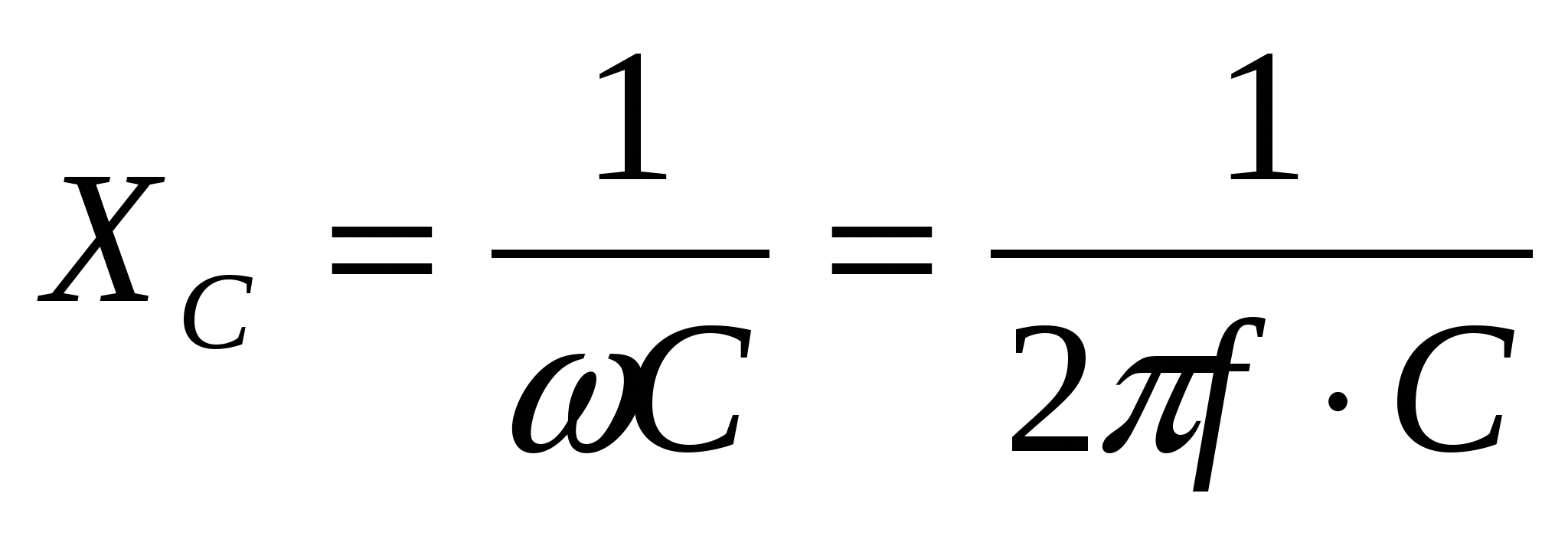 Где: ХС– емкостное сопротивление, Ом. ω – циклическая частота, рад/с С – емкость конденсатора , Ф "фарад" f– частота тока в цепи, Гц. Из формулы видно, что при повышении частоты тока емкостное сопротивление уменьшается, а при снижении частоты тока – увеличивается. То есть емкостное сопротивление реагирует на частоту тока в цепи, поэтому его еще называют реактивным. Для постоянного тока f =0, поэтому для постоянного тока конденсатор имеет бесконечно большое сопротивление. Емкость конденсатора зависит от площади пластин, толщины диэлектрика и его диэлектрической проницаемости. Цепь, содержащая емкость, является искусственной, так как реальный конденсатор кроме емкостного сопротивления содержит активное сопротивление R. Но мы рассмотрим идеальный конденсатор, в котором активное сопротивление R=0. В отдельных случаях активным сопротивлением реального конденсатора можно пренебречь из-за его малости. б) Ток и напряжение в цепи переменного тока с конденсатором.  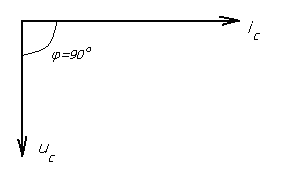 а) Схема цепи с конденсатором б) Векторная диаграмма. 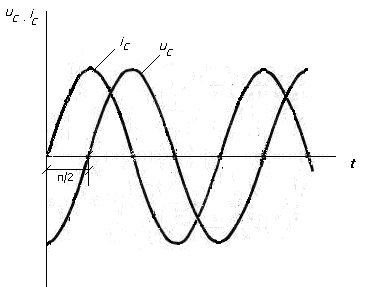 в) Графики тока и напряжения в цепи с емкостью Рис.40 1. Электрическая цепь с конденсатором. При прохождении синусоидального тока 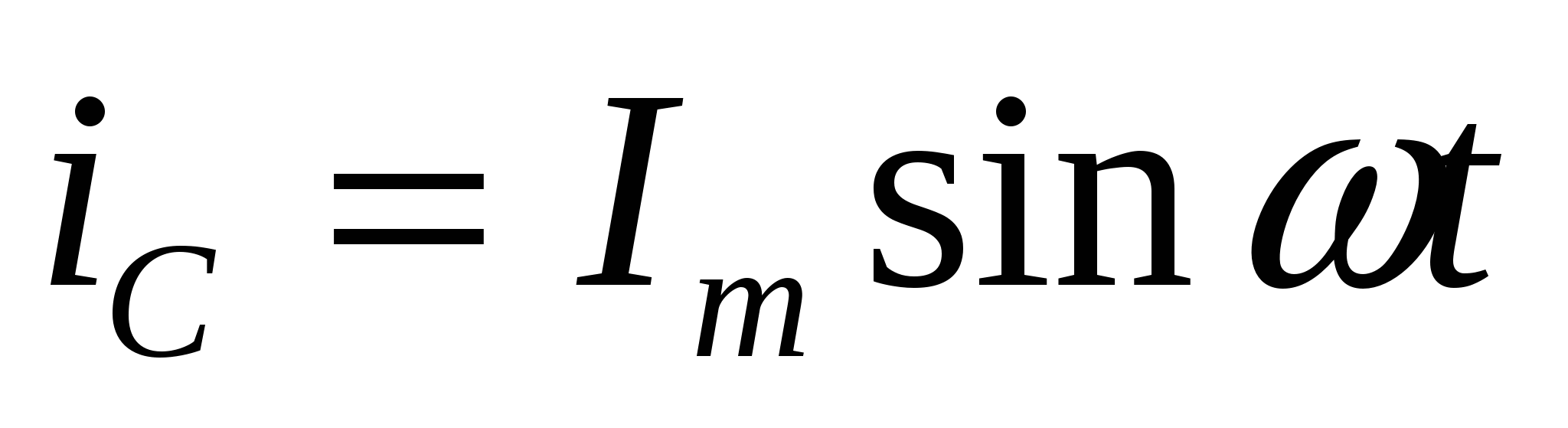 напряжение на катушке будет равно 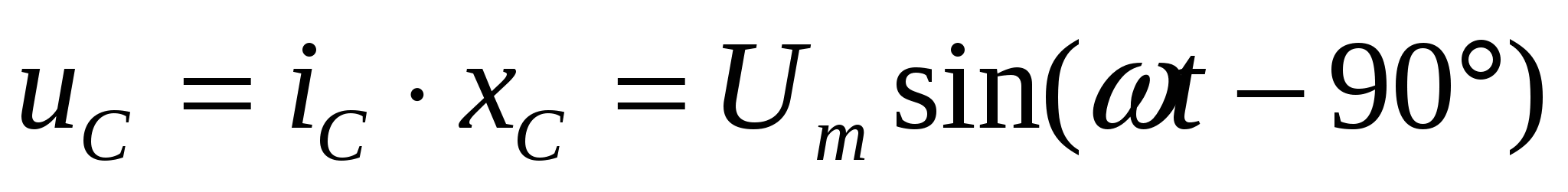 , ,то есть напряжение на конденсаторе отстает от тока по фазе на угол 90° (π /2). Занятие 41 Цепь с последовательным соединением RL и RC а) Последовательное соединение индуктивности и активного сопротивления Реальная катушка имеет активное и индуктивное сопротивления. 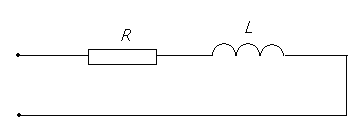 Рис.41.1 Электрическая цепь реальной катушки индуктивности Построим векторную диаграмму и графики для этого случая. 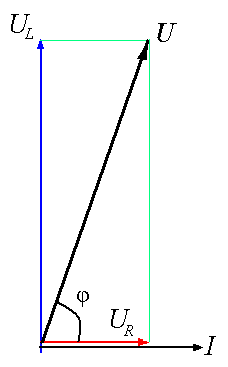 Рис.41.2. Векторная диаграмма для цепи с последовательным соединением R и L. На рис.41.2 векторIобозначает переменный ток катушки. Часть напряжения сети, падающая в сопротивлении R изображена вектором UR,совпадающим по фазе с током. Напряжение на индуктивности показано вектором UL, который опережает ток на угол 90о . Напряжение сети U должно быть равно геометрической сумме активного URtи индуктивного UL падений напряжения. Для получения геометрической суммы необходимо на векторах URи ULпостроить параллелограмм. Его диагональ (равнодействующая) даст напряжение сети U. Ток в цепи с последовательно соединенными активным сопротивлением и индуктивностью будет иметь одно и то же значение. Поэтому, разделив величины векторов напряжений на одно и то же значение тока, мы получим значения сопротивлений цепи. Они образуют треугольник сопротивлений 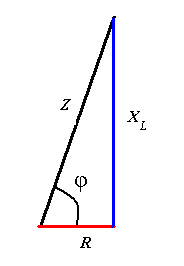 Рис.41.3. Треугольник сопротивлений Из треугольника сопротивлений следует, что Где: Z- полное сопротивление цепи (Ом) R - активное сопротивление цепи (Ом) XL - индуктивное сопротивление цепи (Ом) б) Последовательное соединение емкости и активного сопротивления Реальный конденсатор имеет активное и емкостное сопротивления. 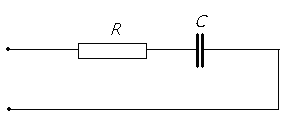 Рис.41.4. Электрическая цепь реального конденсатора Построим векторную диаграмму и графики для этого случая. На рис.41.5 векторIобозначает переменный ток катушки. Часть напряжения сети, падающая в сопротивлении R изображена вектором UR,совпадающим по фазе с током. Напряжение на индуктивности показано вектором UС, который отстает от тока на угол 90о . Напряжение сети U должно быть равно геометрической сумме активного URtи емкостного UС падений напряжения. Для получения геометрической суммы необходимо на векторах URи UСпостроить параллелограмм. Его диагональ (равнодействующая) даст напряжение сети U. 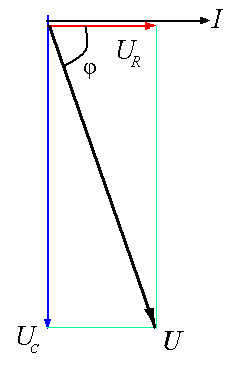 Рис.41.5. Векторная диаграмма для цепи с последовательным соединением R и С. Ток в цепи с последовательно соединенными активным сопротивлением и емкостью будет иметь одно и то же значение. Поэтому, разделив величины векторов напряжений на одно и то же значение тока, мы получим значения сопротивлений цепи. Они образуют треугольник сопротивлений 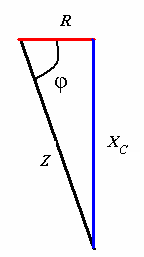 Рис.41.6. Треугольник сопротивлений Из треугольника сопротивлений следует, что Где: Z- полное сопротивление цепи (Ом) R - активное сопротивление цепи (Ом) XС - емкостное сопротивление цепи (Ом) Занятие 42 . Комплексный метод расчета цепей переменного тока. а) Понятие о комплексных числах Векторное представление синусоидальных величин позволяет заменить сложные математические операции с синусоидальными величинами простыми операциями с векторами. Однако геометрические операции с векторами не обладают высокой точностью. Поэтому геометрические операции с векторами заменяют алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов. Векторы можно изображать не только на плоскости хОу, но и на комплексной плоскости в виде комплексного числа. Комплексное число состоит из вещественной (действительной) (X) и мнимой частей.(Yj) Алгебраическая форма комплексного числа имеет вид: z= x + yi, На графиках по оси абсцисс откладывают действительную часть, а по оси ординат — мнимую часть комплексного числа. Действительную ось обозначают +1 и -1, а мнимую ось + j и – j Каждой точке (x , y) координатной плоскости, изображающей комплексное число z = x + yi, соответствует единственный вектор, отложенный от начала системы координат и обратно (рис.42.1). При этом двум различным точкам координатной плоскости будут соответствовать два таких различных вектора. Таким образом, может быть установлено однозначное соответствие между множеством точек координатной плоскости (комплексными числами) и множеством векторов, отложенных от начала системы координат. 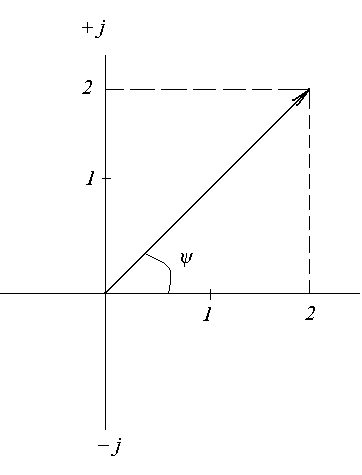 Рис.42.1. Геометрическое представление комплексного числа на плоскости Н 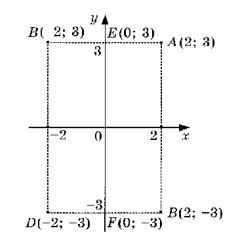 а рис. 42.2 изображена координатная плоскость. а рис. 42.2 изображена координатная плоскость.Числу 2 + 3i соответствует точка A(2, 3) плоскости; числу 2 – 3i – точка B(2, – 3); числу – 2 + 3i – точка C(– 2, 3); числу – 2 – 3i – точка D(– 2; – 3). Числу 3i соответствует точка E(0, 3); а числу – 3i – точка F(0, – 3). рис. 42.2 координатная плоскость Итак, каждому комплексному числу соответствует единственная точка координатной плоскости и, обратно, каждой точке координатной плоскости соответствует единственное комплексное число, при этом двум различным комплексным числам соответствуют две различные точки координатной плоскости. Ясно, что действительным числам x + 0i соответствуют точки оси абсцисс, а чисто мнимым числам 0 + yi, где y = 0 – точки оси ординат. Поэтому ось Oy называют мнимой, а ось Ox – действительной б) Формы записи комплексных чисел. Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в : показательной тригонометрической алгебраической формах. Пусть дано число вращающимся вектором (см. рис. 42.3) 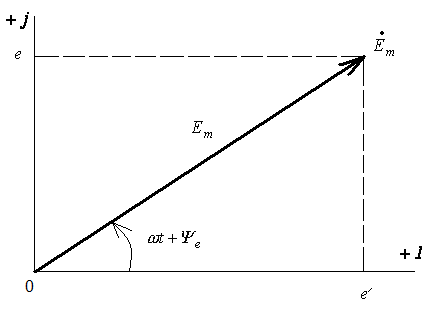 Рис.42.3. Представление числа на координатной плоскости Тогда в показательной форме это число будет выглядеть как в в алгебраической Модулем комплексного числа называется длина вектора OP (см. рис.42.4) , изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается | a+ bi | или буквой r и равен 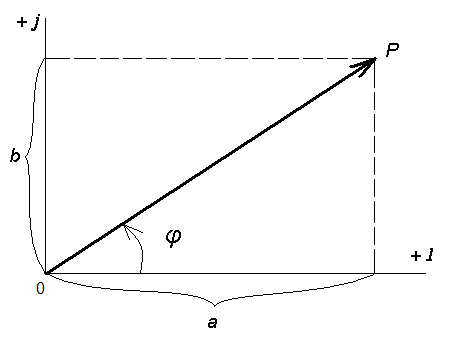 Рис.42.4. Представление комплексных чисел на плоскости Аргумент комплексного числа - это уголφ между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tg φ = b / a . Тригонометрическая форма комплексного числа. Абсциссу a и ординату b комплексного числа a+ bi можно выразить через его модуль r и аргумент φ: 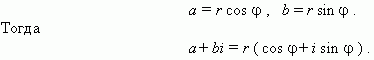 Занятие 43 Комплексные сопротивления и проводимости В общем случае цепи переменного тока характеризуются несколькими сопротивлениями:
Комплексное полное сопротивление цепи определяется выражениями: Где: Z – полное сопротивление цепи (модуль комплексного сопротивления) R – активное сопротивление цепи XL - индуктивное сопротивление цепи XC - емкостное сопротивление цепи X = XL - XC - реактивное сопротивление цепи φ – аргумент комплексного сопротивления Полное сопротивление цепи (модуль комплексного сопротивления) определяется по формуле: Аргумент комплексного сопротивления определяется по формуле: Величина, обратная полному сопротивлению называется комплексной проводимостью. Где: Y - полная проводимость цепи, (1/Ом) G - активная проводимость цепи, (1/Ом) B - реактивная проводимость, (1/Ом) Активная проводимость определяется Реактивная проводимость определяется Занятие 44 Резонанс напряжений Схема последовательного соединения активного сопротивления, катушки индуктивности и конденсатора приведена на рис.44.1. 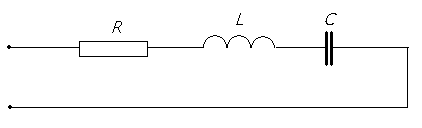 Рис. 44.1. Схема последовательного соединения активного сопротивления, катушки индуктивности и конденсатора При последовательном соединении трех элементов R, L, C векторная диаграмма выглядит следующим образом: вектор тока в цепи Iотложен горизонтально, с ним совпадает вектор напряжения на активном сопротивлении UR , вектор напряжения на индуктивности U L направлен вверх, а вектор напряжения на емкости UC направлен вниз. 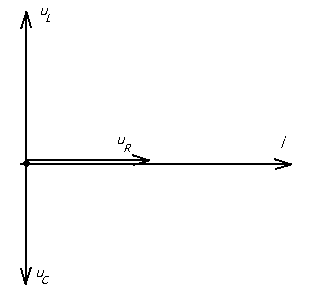 Рис.44.2. Векторная диаграмма напряжений при последовательном соединении активного сопротивления, катушки индуктивности и конденсатора. Если падение напряжения на индуктивном сопротивлении больше, чем на емкостном, то результирующий вектор будет опережать вектор тока на какой-то угол φ. В этом случае говорят, что цепь имеет индуктивный характер. (см.рис.44.3.) 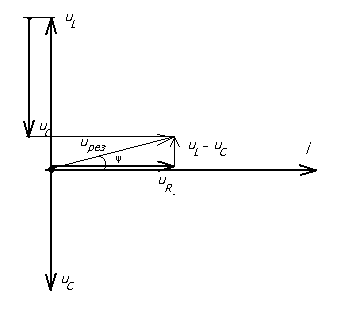 Рис.44.3. Векторная диаграмма цепи с индуктивным характером. Если падение напряжения на емкостном сопротивлении больше, чем на индуктивном, то вектор результирующего напряжения будет отставать от вектора тока на какой –то угол φ. В этом случае говорят, что цепь носит емкостный характер. (см. рис.44. 4.) 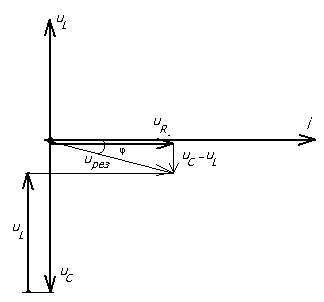 Рис.44.4. Векторная диаграмма цепи с емкостным характером. В общем случае уравнение напряжений в цепи будет равно: а уравнение сопротивлений : Особенностью последовательного соединения активного сопротивления, емкости и индуктивности является возможность возникновения резонанса напряжений. Представим, что в цепи с последовательно соединенными активным сопротивлением, емкостью и индуктивностью, частота тока увеличивается от частоты f1 до частоты f2. (см. рис. 44.5.) 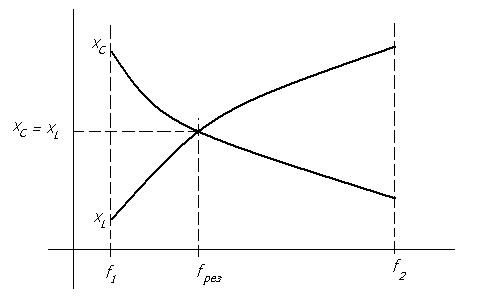 Рис.44.5. Изменение реактивных сопротивлений при изменении частоты тока. При увеличении частоты тока в цепи емкостное сопротивление уменьшается, а индуктивное увеличивается. При каком – то значении частоты тока емкостное сопротивление становится равным индуктивному сопротивлению. Эта частота называется резонансной. Явления, происходящие в цепи с последовательно соединенными R,L,C при резонансной частоте называются резонансом напряжения. При резонансе напряжение на емкости UC равно напряжению на индуктивности U L . Но так как они находятся в противофазе друг другу сумма их равна нулю. Условием резонанса является равенство реактивных сопротивлений XL = XC или Отсюда значение резонансной частоты определиться Когда цепь не настроена в резонанс , ее полное сопротивление определяется соотношением: Таким образом полное сопротивление цепи при резонансе оказывается равным активному сопротивлению. Уменьшение полного сопротивления цепи приводит к тому, что сила тока в ней возрастает. .На векторной диаграмме при резонансе (см.рис.44. 6) векторы напряжений на реактивных элементах равны друг другу и направлены в противоположные стороны. т. е. сдвинуты по фазе относительно друг друга на угол 180 градусов. Угол сдвига фаз между током и напряжением в сети равен нулю. 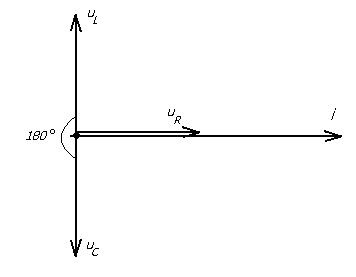 Рис.44.6. Векторная диаграмма при резонансе напряжений. 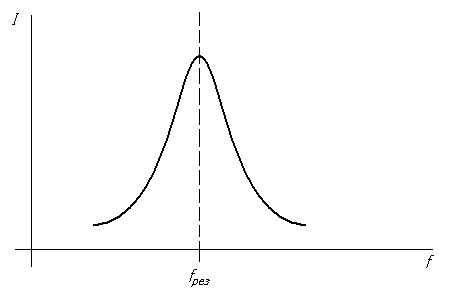 Рис.44.7. Изменение тока в цепи при резонансе. Занятие 45 Параллельное соединение L и C. Резонанс токов. В цепи переменного тока, в которой индуктивность и емкость соединены параллельно (см.рис.45.1.) может возникнуть резонанс токов. 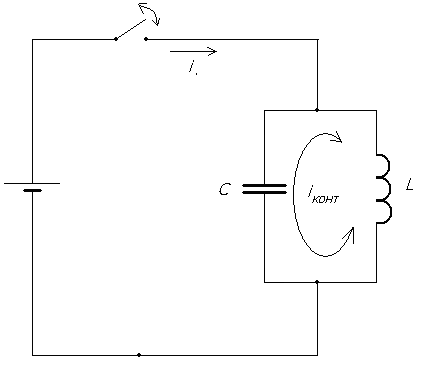 Рис.45.1. Схема цепи с параллельно соединенными емкостью и индуктивностью. В результате резонанса токов общий ток в цепи может быть относительно мал, а в контуре индуктивности и емкости, где происходят электрические колебания, протекает переменный ток , значительно больше общего. Для понимания сущности резонанса токов выясним, как получаются электрические колебания в цепи, состоящей из параллельно соединенных индуктивности и емкости. Рассмотрим работу схемы. При подаче напряжения в схему конденсатор заряжается до напряжения источника электрической энергии. Разорвем внешнюю цепь заряда конденсатора. Так как конденсатор остался соединенным с катушкой и является источником электрической энергии, то он начинает разряжаться через витки катушки индуктивности. По катушке протекает ток разряда, в результате которого появляется магнитное поле. Ток будет возрастать постепенно и достигнет наибольшей величины в тот момент, когда конденсатор разрядится. К этому моменту времени энергия электрического поля конденсатора превратится в энергию магнитного поля катушки индуктивности. Далее запасенная в катушке энергия магнитного поля переходит в энергию электрического поля конденсатора, перезаряжая его через замкнутую цепь. Так этот процесс будет повторяться периодически. Таким образом, в контуре с параллельно соединенными емкостью и индуктивностью возникнут свободные электрические колебания. Поэтому такой контур называют колебательным. Для возникновения колебаний необходимо первоначально зарядить конденсатор от внешнего источника электрической энергии. В идеальном колебательном контуре R=0. При резонансе XL =XC. Или Это значение частоты в контуре называется резонансной частотой. При этой частоте в контуре будут протекать токи значительно бо̀льшие по величине, чем во внешней цепи. Из формулы следует, что изменяя величину емкости или индуктивности можно изменять (настраивать) контур на определенную частоту колебаний . В реальном колебательном контуре колебания всегда затухающие. Это объясняется тем, что проводники реального контура всегда имеют активное сопротивление, поэтому часть энергии колебаний превращается в тепловую энергию и уходит в пространство уменьшая тем самым величину электрической энергии колебаний. Для поддержания колебаний в контуре его соединяют с генератором колебаний. тогда колебания в контуре называются вынужденными. Занятие 46 Активная, реактивная и полная мощности. В отличии от постоянного тока, в переменном токе рассматриваются три вида мощности:
Полная мощность генератора переменного тока расходуется на активную и реактивную мощность. Активная мощность , расходуемая в активном сопротивлении, преобразуется в полезную работу или тепло, рассеиваемое в пространство. Реактивная мощность обусловлена колебаниями энергии при создании и исчезновении электрических и магнитных полей. Эта энергия то запасается в полях реактивных сопротивлений. то возвращается генератору, включенному в цепь. Связь между полной, активной и реактивной мощностями определяется из треугольника мощностей (см.рис.46.1.). 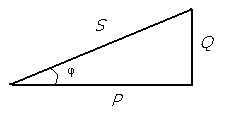 Рис.46. 1. Треугольник мощностей. Из треугольника : Занятие 47 Коэффициент мощности Коэффициентом мощности или cos φ электрической сети называется отношение активной мощности к полной мощности. Коэффициент мощности можно определить как расчетным путем, так и измерить специальными приборами. Только в том случае, когда нагрузка имеет исключительно активный характер, cos φ равен единице. В основном же, активная мощность меньше полной и поэтому коэффициент мощности меньше единицы. Чем меньше коэффициент мощности сети, тем менее загружена сеть активной мощностью и тем меньше коэффициент полезного действия использования сети. В связи с этим необходимо, чтобы как можно большую часть в полной мощности составляла именно активная мощность, а не реактивная, в этом случае коэффициент мощности будет ближе к единице. Причины низкого коэффициента мощности:
Для увеличения коэффициента мощности можно:
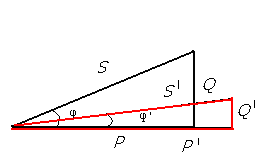 Рис.47.1. Уменьшение реактивной мощности, уменьшение угла φ. увеличение cos φ. Занятие 48 Контрольная работа №7 ЭТ У48 Контрольные вопросы:
R L C с индуктивным характером цепи.
R L C с емкостным характером цепи.
Примечание: Каждому студенту необходимо решить задачу, предложенную преподавателем. |
