Задание 2 Свиридов А.А. Программа среднего профессионального образования 40. 02. 01 Право и организация социального обеспечения Дисциплина Математика Практическое задание 2
 Скачать 51.68 Kb. Скачать 51.68 Kb.
|
|
АНО ПО «Открытый социально-экономический колледж» Программа среднего профессионального образования 40.02.01 Право и организация социального обеспечения Дисциплина: Математика Практическое задание №2 Выполнил: слушатель Свиридов Александр Александрович Преподаватель: Васильцова Анна Сергеевна  Задание №1 1. Решить уравнение методом Гаусса:  - Перепишем систему в матричном виде и решим его методом Гаусса:  - от 2 строки отгимаем 1 строку, умноженную на 3; от 3 строки отнимаем первую строку, умноженную на 5 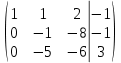 - вторую строку делим на -1  - от 1 строки отнимаем 2 строку, умноженную на 1; к 3 строке добавляем 2 строку, умноженную на 2  - 3 строку делим на 10  - к 1 строке добавляем 3 строку, умноженную на 6; от 2 строки отнимаем 3 строку, умноженную на 8  - получаем решение 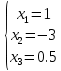 2. Решить уравнение методом Крамера:  - воспользуемся формулой для вычисления определителя матрицы 3х3  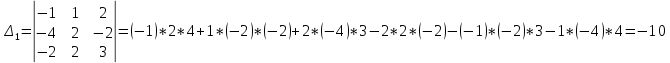   Отсюда следует: 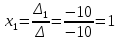 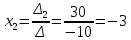  Задание №2 Решить систему линейных уравнений  Решение: - Перепишем систему в матричном виде и решим его методом Гаусса:  - для удобства вычислений поменяем строки местами  - умножаем 2-ю строку на -1/2 и добавим к 3-й:  - умножаем 1-ю строку на -2/3 и добавим ко второй:  - для удобства вычислений поменяем строки местами:  - умножаем 2-ю строку на 14/15 и добавляем к 3-й: 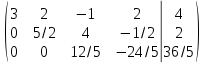 - получим единицы на главной диагонали. Для этого всю строку на соответствующий элемент главной диагонали:  Теперь исходную систему можно записать как: 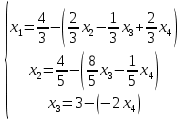 Переменная x4 является свободной, через нее выразим остальные переменные. Для получения частного решения, приравняем x4 к 0:  Новомосковск 2022г. |
