3) контрольная №1 вариант 1. Задача 1. Найти произведение матриц Решение Задача 2. Вычислить определитель тремя способами
 Скачать 49.71 Kb. Скачать 49.71 Kb.
|
|
Контрольная работа 1. Линейная алгебра Задача №1. Найти произведение матриц 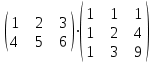 Решение: 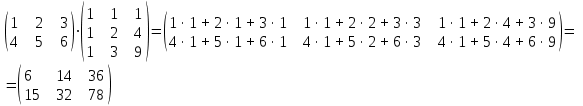 Задача №2. Вычислить определитель тремя способами: а) разложив его по элементам i-й строки; б) разложив его по элементам j-го столбца; в) получив предварительно нули в i-й строке. 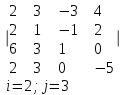 Решение: а) вычисляем определитель, разложив его по элементам 2-й строки: 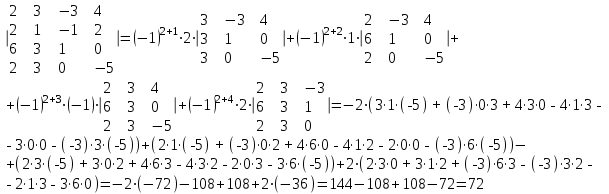 б) вычисляем определитель, разложив его по элементам 3-го столбца: 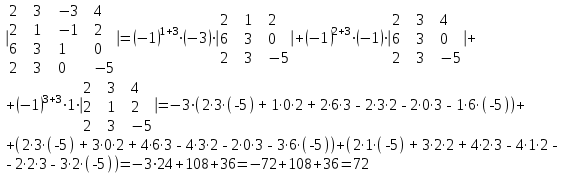 в) вычисляем определитель, получив предварительно нули во 2-й строке: 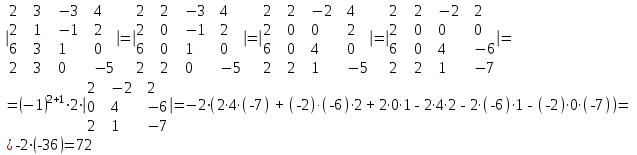 Задача №3. Вычислить ранг матрицы с помощью элементарных преобразований 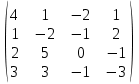 Решение: Поменяем местами 1 и 2 строки матрицы и приведем матрицу к ступенчатому виду элементарными преобразованиями: 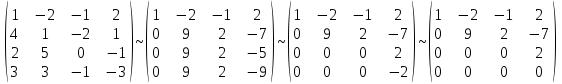 т.к. ненулевых строк 3, то ранг матрицы равен 3. Задача №4. Решить матричное уравнение и сделать проверку 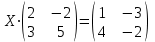 Решение: Пусть 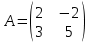 , , 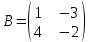 . Матричное уравнение имеет вид: . Матричное уравнение имеет вид: 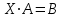 , решение которого находится по формуле: , решение которого находится по формуле: 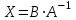 . Находим матрицу . Находим матрицу 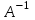 : :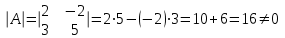 , значит, обратная матрица существует. , значит, обратная матрица существует.Находим дополнительные миноры и алгебраические дополнения матрицы А: 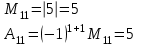 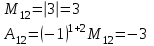 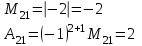 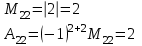 Получаем матрицу алгебраических дополнений: 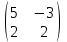 , , 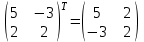 . .Обратная матрица: 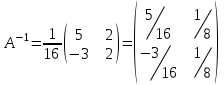 Тогда решение уравнения: 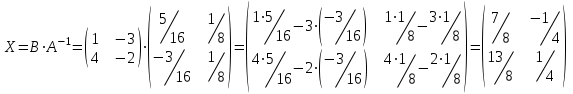 Сделаем проверку: 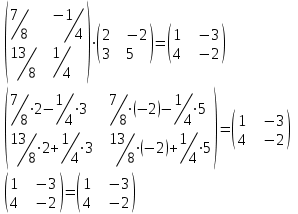 Верно. |
