Контрольная работа по математике. ИТОГОВОЕ ЗАДАНИЕ. Решение Найдите произведение матриц AB. Существует ли произведение матриц BA Почему, Решение
 Скачать 94.27 Kb. Скачать 94.27 Kb.
|
|
ИТОГОВОЕ ЗАДАНИЕ№1 1.Вычислить определитель 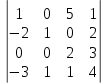 Решение: 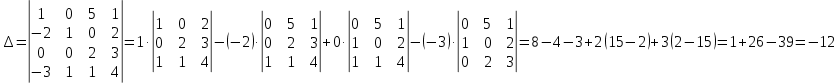 2. Найдите произведение матриц A∙B. Существует ли произведение матриц B∙A? Почему? 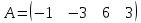 , , 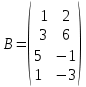 Решение: Компоненты матрицы С вычисляются следующим образом: c11 = a11 · b11 + a12 · b21 + a13 · b31 + a14 · b41 = (-1) · 1 + (-3) · 3 + 6 · 5 + 3 · 1 = (-1) - 9 + 30 + 3 = = 23 c12 = a11 · b12 + a12 · b22 + a13 · b32 + a14 · b42 = (-1) · 2 + (-3) · 6 + 6 · (-1) + 3 · (-3) = (-2) - 18 - 6 - 9 = = -35 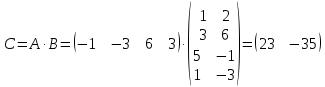 Произведение матриц B∙A не существует, так как количество столбцов матрицы А не равно количеству строк матрицы В. 3.Решите систему линейных уравнений способами: а) по формулам Камера; б) с помощью обратной матрицы 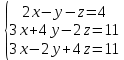 Решение: а) Решим систему по формулам Камера 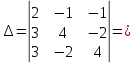 = 2·4·4 + (-1)·(-2)·3 + (-1)·3·(-2) - (-1)·4·3 - 2·(-2)·(-2) - (-1)·3·4 = 32 + 6 + 6 + 12 - 8 + 12 = 60 = 2·4·4 + (-1)·(-2)·3 + (-1)·3·(-2) - (-1)·4·3 - 2·(-2)·(-2) - (-1)·3·4 = 32 + 6 + 6 + 12 - 8 + 12 = 60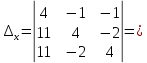 4·4·4 + (-1)·(-2)·11 + (-1)·11·(-2) - (-1)·4·11 - 4·(-2)·(-2) - (-1)·11·4 = 64 + 22 + 22 + 44 - 16 + 44 = 180 4·4·4 + (-1)·(-2)·11 + (-1)·11·(-2) - (-1)·4·11 - 4·(-2)·(-2) - (-1)·11·4 = 64 + 22 + 22 + 44 - 16 + 44 = 180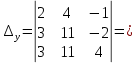 2·11·4 + 4·(-2)·3 + (-1)·3·11 - (-1)·11·3 - 2·(-2)·11 - 4·3·4 = 88 - 24 - 33 + 33 + 44 - 48 = 60 2·11·4 + 4·(-2)·3 + (-1)·3·11 - (-1)·11·3 - 2·(-2)·11 - 4·3·4 = 88 - 24 - 33 + 33 + 44 - 48 = 60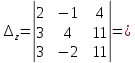 2·4·11 + (-1)·11·3 + 4·3·(-2) - 4·4·3 - 2·11·(-2) - (-1)·3·11 = 88 - 33 - 24 - 48 + 44 + 33 = 60 2·4·11 + (-1)·11·3 + 4·3·(-2) - 4·4·3 - 2·11·(-2) - (-1)·3·11 = 88 - 33 - 24 - 48 + 44 + 33 = 60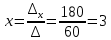 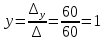 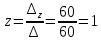 Решение системы: 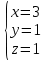 б) Решим систему с помощью обратной матрицы 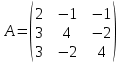 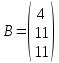 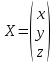 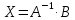 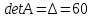 Определитель матрицы А отличен от нуля, следовательно обратная матрица A-1 существует. Для вычисления обратной матрицы найдем дополнительные миноры и алгебраические дополнения матрицы А. Найдем миноры M и алгебраическое дополнение A. 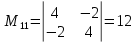 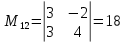 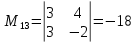 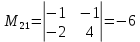 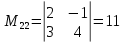 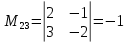 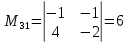 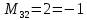 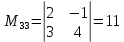 Матрица алгебраических дополнений 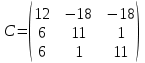 Транспонированная матрица алгебраических дополнений 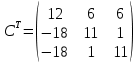 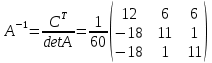 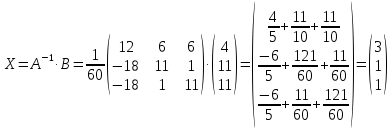 Решение системы: 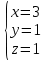 4.Решите матричное уравнение 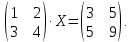 Решение: 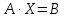 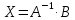 Имеем 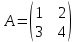 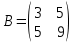 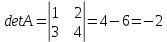 Так как A невырожденная матрица, то существует обратная матрица A-1. Транспонированная матрица AT. 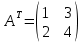
Алгебраические дополнения A11 = (-1)1+1·4 = 4; A12 = (-1)1+2·2 = -2; A21 = (-1)2+1·3 = -3; A22 = (-1)2+2·1 = 1; Обратная матрица A-1. 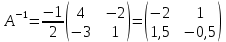 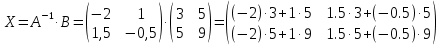 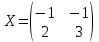 5.Найдите общее решение, построив фундаментальную систему для однородной системы алгебраических уравнений (использовать алгоритм Гаусса) 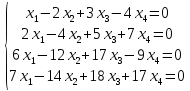 Решение: Перепишем систему уравнений в матричном виде и решим его методом Гаусса 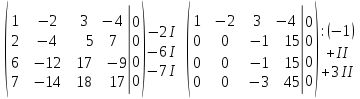 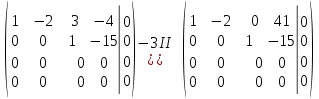 Система имеет множество решений: 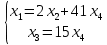 6.Исследовать СЛУ и решить, если она совместима 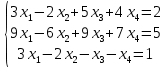 Решение: Исследуем эту систему по теореме Кронекера-Капелли. Выпишем расширенную и основную матрицы: 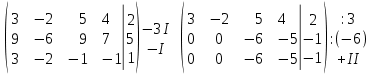 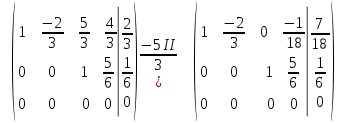 Определим ранг основной системы. 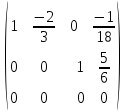 Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля. Ранг этой системы равен rangA=2. Определим ранг расширенной системы. 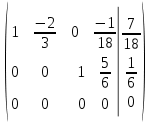
Ранг этой системы равен rangB=2. Ранг матрицы B (rangB=2) равен рангу матрицы A(rangA=2). Система совместна. Решение системы: 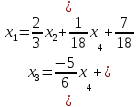 ИТОГОВОЕ ЗАДАНИЕ №2 Выясните образуют ли векторы 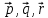 базис. Если образуют, то разложите вектор базис. Если образуют, то разложите вектор 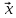 по этому базису. по этому базису. 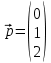 , , 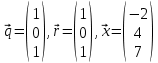 Решение: Проверим образуют ли заданные вектора базис, для этого найдем определитель матрицы: 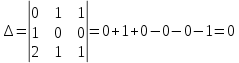 Так как определитель матрицы равен нулю, то введеная система векторов не является базисом. Найдите собственные числа и собственные векторы матрицы A. 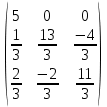 Решение: Составляем систему для определения координат собственных векторов: 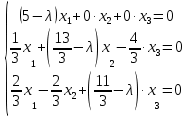 Составляем характеристическое уравнение и решаем его. 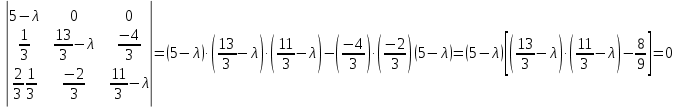 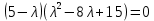 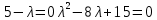 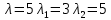 При 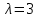 имеем имеем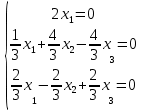 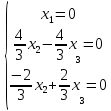 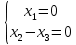 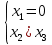 Множество собственных векторов, отвечающих собственному числу λ1 = 3, имеет вид: 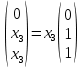 При 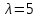 имеем имеем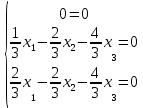 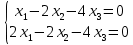 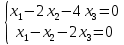 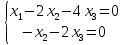 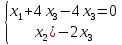 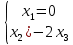 Множество собственных векторов, отвечающих собственному числу λ2,3 = 5, имеет вид: 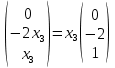 Найдите координаты, модуль и направляющие косинусы вектора 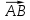 . .A(1; 1; 3), B(2; 2; 3). Решение: Найдем вектор по координатам точек: 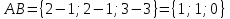 Найдем модуль вектора: 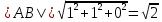 Найдем направляющие косинусы вектора: 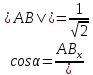 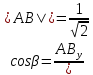 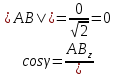 Вычислите скалярное и векторное произведения векторов 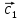 , ,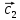 , если , если 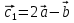 и и 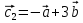 . .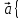 -2; 1; 1}, -2; 1; 1}, 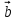 {3; -2; 4} {3; -2; 4}Решение: 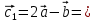 {2·(-2) - 3; 2·1 - (-2); 2·1 - 4} = {-4 - 3; 2 - (-2); 2 - 4} = {-7; 4; -2} {2·(-2) - 3; 2·1 - (-2); 2·1 - 4} = {-4 - 3; 2 - (-2); 2 - 4} = {-7; 4; -2}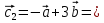 {-(-2) + 3·3; -1 + 3·(-2); -1 + 3·4} = = {2 + 9; -1 + (-6); -1 + 12} = {11; -7; 11} {-(-2) + 3·3; -1 + 3·(-2); -1 + 3·4} = = {2 + 9; -1 + (-6); -1 + 12} = {11; -7; 11} Найдем скалярное произведение векторов: 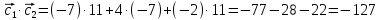 Найдем векторное произведение векторов: 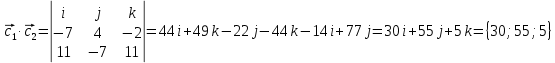 ИТОГОВОЕ ЗАДАНИЕ№3 Решить задачу симплекс-методом. 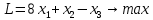 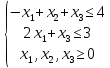 Введем дополнительные переменные 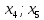 , тогда , тогда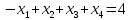 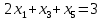 Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом. Решим систему уравнений относительно базисных переменных: x4, x5 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,0,0,4,3) Базисное решение называется допустимым, если оно неотрицательно.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. Определим новую базисную переменную. В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: 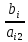 и из них выберем наименьшее: 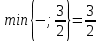 Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (2) и находится на пересечении ведущего столбца и ведущей строки.
Формируем следующую часть симплексной таблицы. Вместо переменной x5 в план 1 войдет переменная x1. Строка, соответствующая переменной x1 в плане 1, получена в результате деления всех элементов строки x5 плана 0 на разрешающий элемент РЭ=2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x1 записываем нули. Таким образом, в новом плане 1 заполнены строка x1 и столбец x1. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. |