Контрольная работа по математике. ИТОГОВОЕ ЗАДАНИЕ. Решение Найдите произведение матриц AB. Существует ли произведение матриц BA Почему, Решение

• Название: Решение Найдите произведение матриц AB. Существует ли произведение матриц BA Почему, Решение
• Анкор: Контрольная работа по математике
• Дата: 26.10.2022
• Размер: 94.27 Kb.
• Имя файла: ИТОГОВОЕ ЗАДАНИЕ.docx
• Тип: Решение; #756607
• страница: 4 из 4

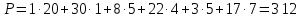Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = х_ij, полагая, что u₁ = 0.

u₁ + v₁ = 1; 0 + v₁ = 1; v₁ = 1

u₁ + v₄ = 5; 0 + v₄ = 5; v₄ = 5

u₃ + v₄ = 7; 5 + u₃ = 7; u₃ = 2

u₃ + v₃ = 4; 2 + v₃ = 4; v₃ = 2

u₂ + v₃ = 5; 2 + u₂ = 5; u₂ = 3

u₂ + v₂ = 1; 3 + v₂ = 1; v₂ = -2

	v1=1			v2=-2			v3=2			v4=5
u1=0	20								3
		1			4			6			5
u2=3			30			8
		3			1	-		5	+		6
u3=2						22			17
		2			5	+		4	-		7

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > x_ij

Выбираем максимальную оценку свободной клетки x₂₄ =6. Строим цикл. Получаем новый опорный план.

ПЛ/ПК		P1		P2		P3		P4
		20		30		30		20
K1	23	20						3
			1		4		6		5
K2	38			30				8
			3		1		5		6
K3	39					30		9
			2		5		4		7

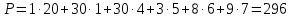Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 1; 0 + v₁ = 1; v₁ = 1

u₁ + v₄ = 5; 0 + v₄ = 5; v₄ = 5

u₂ + v₄ = 6; 5 + u₂ = 6; u₂ = 1

u₂ + v₂ = 1; 1 + v₂ = 1; v₂ = 0

u₃ + v₄ = 7; 5 + u₃ = 7; u₃ = 2

u₃ + v₃ = 4; 2 + v₃ = 4; v₃ = 2

	v1=1			v2=0			v3=2			v4=5
u1=0	20								3
	-	1			4			6	+		5
u2=1			30						8
		3			1			5			6
u3=2						30			9
	+	2			5			4	-		7

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > x_ij

Выбираем максимальную оценку свободной клетки x₃₁ =2. Строим цикл. Получаем новый опорный план.

ПЛ/ПК		P1		P2		P3		P4
		20		30		30		20
K1	23	11						12
			1		4		6		5
K2	38			30				8
			3		1		5		6
K3	39	9				30
			2		5		4		7

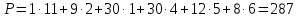Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 1; 0 + v₁ = 1; v₁ = 1

u₃ + v₁ = 2; 1 + u₃ = 2; u₃ = 1

u₃ + v₃ = 4; 1 + v₃ = 4; v₃ = 3

u₁ + v₄ = 5; 0 + v₄ = 5; v₄ = 5

u₂ + v₄ = 6; 5 + u₂ = 6; u₂ = 1

u₂ + v₂ = 1; 1 + v₂ = 1; v₂ = 0

	v1=1			v2=0			v3=3			v4=5
u1=0	11								12
		1			4			6			5
u2=1			30						8
		3			1			5			6
u3=1	9					30
		2			5			4			7

Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_j ≤ х_ij.

Минимальные затраты составят: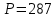

Выводы.

От 1-го поставщика необходимо направить к 1-му потребителю (11 ед.), к 4-му потребителю (12 ед.)

От 2-го поставщика необходимо направить к 2-му потребителю (30 ед.), к 4-му потребителю (8 ед.)

От 3-го поставщика а необходимо направить к 1-му потребителю (9 ед.), к 3-му потребителю (30 ед.)