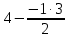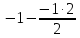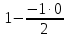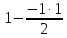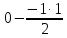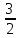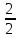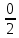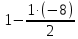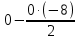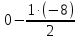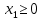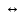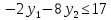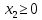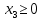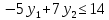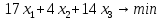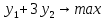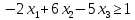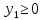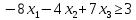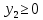Контрольная работа по математике. ИТОГОВОЕ ЗАДАНИЕ. Решение Найдите произведение матриц AB. Существует ли произведение матриц BA Почему, Решение

• Название: Решение Найдите произведение матриц AB. Существует ли произведение матриц BA Почему, Решение
• Анкор: Контрольная работа по математике
• Дата: 26.10.2022
• Размер: 94.27 Kb.
• Имя файла: ИТОГОВОЕ ЗАДАНИЕ.docx
• Тип: Решение; #756607
• страница: 2 из 4

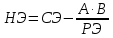СТЭ - элемент старого плана,

РЭ - разрешающий элемент (2),

А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.

Представим расчет каждого элемента в виде таблицы:

B	x1	x2	x3	x4	x5

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5
x4	11/2	0	1	3/2	1	1/2
x2	3/2	1	0	1/2	0	1/2
F(X1)	12	0	-1	5	0	4

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x₃, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: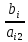
и из них выберем наименьшее: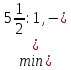

Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (1²/₃) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	min
x4	11/2	0	1	3/2	1	1/2	11/2
x2	3/2	1	0	1/2	0	1/2	-
F(X2)	12	0	-1	5	0	4

Формируем следующую часть симплексной таблицы. Вместо переменной x₄ в план 2 войдет переменная x₂.

Строка, соответствующая переменной x2 в плане 2, получена в результате деления всех элементов строки x4 плана 1 на разрешающий элемент РЭ=1. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули.

Таким образом, в новом плане 2 заполнены строка x2 и столбец x2. Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5
X2	11/2	0	1	3/2	1	1/2
X1	3/2	1	0	1/2	0	1/2
F(X2)	35/2	0	0	13/2	1	9/2

Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.

Окончательный вариант симплекс-таблицы:

Базис	B	x1	x2	x3	x4	x5
X2	11/2	0	1	3/2	1	1/2
X1	3/2	1	0	1/2	0	1/2
F(X)	35/2	0	0	13/2	1	9/2

Оптимальный план можно записать так:

x₁ = 1¹/₂, x₂ = 5¹/₂, x₃ = 0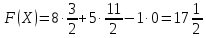

2. 
   Составить для данной задачи линейного программирования двойственную. Решить двойственную задачу графическим методом. Используя теоремы двойственности, найти решения исходной задачи.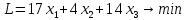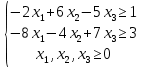
   

Построим двойственную задачу по следующим правилам.

1. 
   Количество переменных в двойственной задаче равно количеству неравенств в исходной.
   
2. 
   Матрица коэффициентов двойственной задачи является транспонированной к матрице коэффициентов исходной.
   
3. 
   Система ограничений двойственной задачи записывается в виде неравенств противоположного смысла неравенствам системы ограничений прямой задачи.
   

Столбец свободных членов исходной задачи является строкой коэффициентов для целевой функции двойственной. Целевая функция в одной задаче максимизируется, в другой минимизируется.

Расширенная матрица A.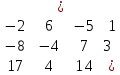



Транспонированная матрица A^T.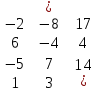



Условиям неотрицательности переменных исходной задачи соответствуют неравенства-ограничения двойственной, направленные в другую сторону. И наоборот, неравенствам-ограничениям в исходной соответствуют условия неотрицательности в двойственной.

Неравенства, соединенные стрелочками (↔), называются сопряженными.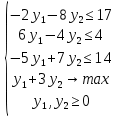

Исходная задача		Двойственная задача

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

Построим уравнение -2y₁-8y₂ = 17 по двум точкам.

y1	y2
0	2,13
-8,5	0

Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:-2 ⸱0 - 8 ⸱ 0 - 17 ≤ 0, т.е. -2у₁-8у₂ - 17≤ 0 в полуплоскости ниже прямой.

Построим уравнение 6y₁-4y₂ = 4 по двум точкам.

y1	y2
0	-1
0,67	0

Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:6 ⸱ 0 - 4 ⸱ 0 - 4 ≤ 0, т.е. 6у₁-4у₂ - 4≤ 0 в полуплоскости ниже прямой.

Построим уравнение -5y₁+7y₂ = 14 по двум точкам.

y1	y2
0	2
-2,8	0

Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:-5 ⸱ 0 + 7 ⸱ 0 - 14 ≤ 0, т.е. -5x₁+7x₂ - 14≤ 0 в полуплоскости ниже прямой.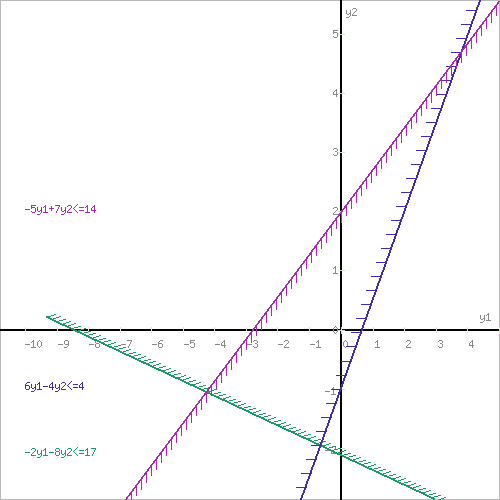



Рассмотрим целевую функцию задачи F = 2y₁+5y₂ → max.

Построим прямую, отвечающую значению функции F = y₁+3y₂ → max.
Построим прямую, отвечающую значению функции F = y₁+3y₂ = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (1;3). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.