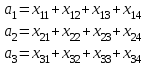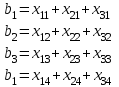Контрольная работа по математике. ИТОГОВОЕ ЗАДАНИЕ. Решение Найдите произведение матриц AB. Существует ли произведение матриц BA Почему, Решение

• Название: Решение Найдите произведение матриц AB. Существует ли произведение матриц BA Почему, Решение
• Анкор: Контрольная работа по математике
• Дата: 26.10.2022
• Размер: 94.27 Kb.
• Имя файла: ИТОГОВОЕ ЗАДАНИЕ.docx
• Тип: Решение; #756607
• страница: 3 из 4

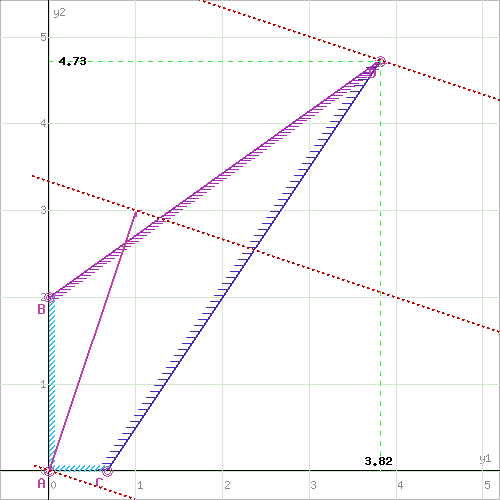Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых (2) и (3), то ее координаты удовлетворяют уравнениям этих прямых:

6y₁-4y₂=4

-5y₁+7y₂=14

Решив систему уравнений, получим: y₁ = 3.8182, y₂ = 4.7273

Откуда найдем максимальное значение целевой функции:

F(X) = 1⸱3.8182 + 3⸱4.7273 = 18

Используя теоремы двойственности, найдем решения исходной задачи.

Из теоремы двойственности следует, что Y = C*A^-1.

Составим матрицу A из компонентов векторов, входящих в оптимальный базис.

A = (A2, A3) =	6 -5 -4 7

Определив обратную матрицу D = А^-1 через алгебраические дополнения, получим:

D = A-1 =

7/22 5/22 2/11 3/11

Обратная матрица A^-1 расположена в столбцах дополнительных переменных.

Тогда Y = C*A-1 = (4, 14) ·

7/22 5/22 2/11 3/11

= (42/11;52/11)

Оптимальный план двойственной задачи равен:
y₁ = 3⁹/₁₁, y₂ = 4⁸/₁₁

F(Y) = 1·3⁹/₁₁+3·4⁸/₁₁ = 18

3. 
   Решить методом потенциалов транспортную задачу
   
4. 
   
   

1	4	6	5	23
3	1	5	6	38
2	5	4	7	39
20	30	30	20

_{Решение:}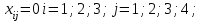

По запасам:

По потребностям:

Проверим необходимое и достаточное условие разрешимости задачи.

∑a = 23 + 38 + 39 = 100; ∑b = 20 + 30 + 30 + 20 = 100

Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.

Используя метод северо-западного угла, построим первый опорный план транспортной задачи. План начинается заполняться с верхнего левого угла.

ПЛ/ПК		P1		P2		P3		P4
		20		30		30		20
K1	23	20		3
			1		4		6		5
K2	38			27		11
			3		1		5		6
K3	39					19		20
			2		5		4		7

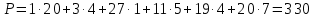Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 1; 0 + v₁ = 1; v₁ = 1

u₁ + v₂ = 4; 0 + v₂ = 4; v₂ = 4

u₂ + v₂ = 1; 4 + u₂ = 1; u₂ = -3

u₂ + v₃ = 5; -3 + v₃ = 5; v₃ = 8

u₃ + v₃ = 4; 8 + u₃ = 4; u₃ = -4

u₃ + v₄ = 7; -4 + v₄ = 7; v₄ = 11

	v1=1			v2=4			v3=8			v4=11
u1=0	20		3
		1			4			6			5
u2=-3			27			11
		3			1			5			6
u3=-4						19			20
		2			5			4			7

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > x_ij

Выбираем максимальную оценку свободной клетки x₁₄ =5. Строим цикл.

ПЛ/ПК		P1		P2		P3		P4
		20		30		30		20
K1	23	20		3
			1	-	4		6	+	5
K2	38			27		11
			3	+	1	-	5		6
K3	39					19		20
			2		5	+	4	-	7

Получаем новый опорный план

ПЛ/ПК		P1		P2		P3		P4
		20		30		30		20
K1	23	20						3
			1		4		6		5
K2	38			30		8
			3		1		5		6
K3	39					22		17
			2		5		4		7