математика практическое 6. Математика Практическое занятие 6. Программа среднего профессионального образования 44. 02. 01 Дошкольное образование Дисциплина Математика. Практическое занятие 6 Преподаватель
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
|
Задание 9. Вычислите предложенные неопределенные интегралы, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты). 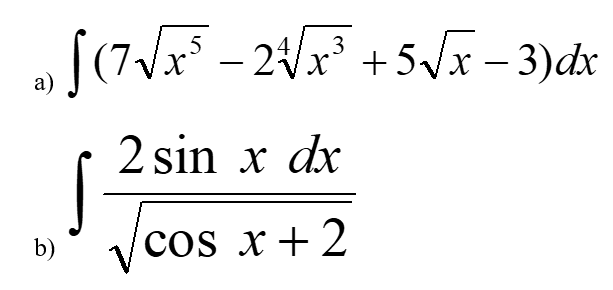 Решение:  Представим исходный интеграл, как сумму интегралов: Поочередно решим каждый интеграл, используя свойства интегралов: 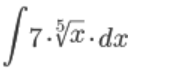 Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции. Также представим подкоренное выражение в виде значении со степенью: Интеграл от хn есть 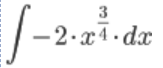 Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции. Также представим подкоренное выражение в виде значении со степенью: Интеграл от хn есть 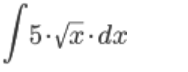 Интеграл от хn есть 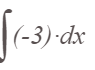 Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции. 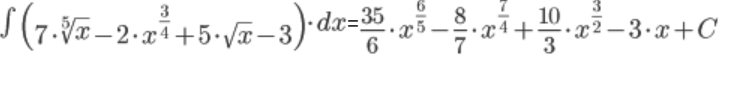  Выражение -sin(x) подведем под знак дифференциала, т.е.: (-sin(x))·dx=d (cos(x)); t=cos(x) Тогда исходный интеграл можно записать так: Делаем замену переменных: u=t+2 Тогда, по таблице простейших интегралов: Возвращаемся к t: Чтобы записать окончательный ответ, осталось вместо t подставить cos(x): Задание 10. Вычислите площадь предложенной криволинейной трапеции, ограниченной графиками функций f(x) и g(x), подробно описывая ход решения (указывайте формулы, которыми пользуетесь, отобразите графики функций и получившуюся фигуру, записывайте промежуточные результаты):  Решение: График функции f(x)=x–1 – прямая. строим по двум точкам (0;–1) и (1;0) График функции g(x)=x2–4x+3 – парабола, ветви вверх, вершина в точке (2; –1) Найдем абсциссы точек пересечения графиков. Для этого приравняем значения с «х» друг к другу. x–1=x2–4x+3 x2–5x+4=0. Получается квадратное уравнение. Находим дискриминант: D=(5)2-4*1*3=25–16=9 Находим корни уравнения по формуле, используя дискриминант: x1=1; x2=4 Применяем формулу: S= =(5  Задание 11. Решите предложенную задачу, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, отобразите графически полученное решение): Найдите объем многогранника, вершинами которого являются точки A, A1, B1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 6 см2, а боковое ребро равно 4 см. Решение: В основаниях призмы Δ АВС и Δ A1B1C1 По условию Sосн=SΔ АВС =SΔ A1B1C1 A A1=ВВ1=СС1=Hпризмы=4 В основании пирамиды A A1B1C1 Δ A1B1C1 Hпирамиды=Hпризмы=4 Vпирамиды A A1B1C1=(1/3)Sосн·H=(1/3)·6·4=8 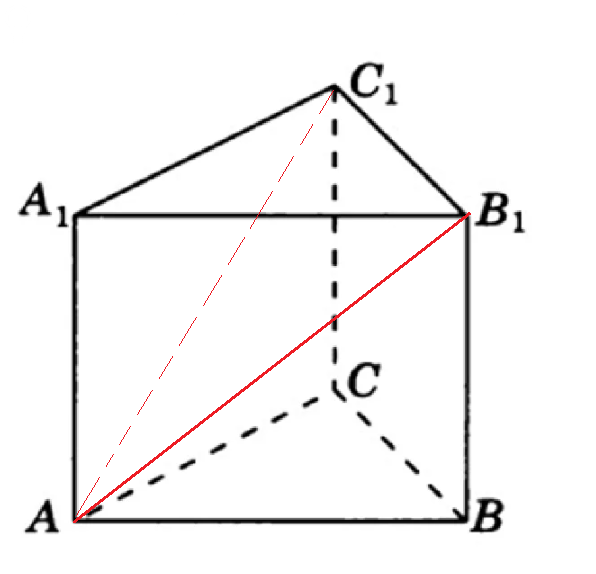 Задание 12. Задание 12. Изучите предложенные исходные данные, полученные при измерении:
Выполните задания с учетом исходных данных, подробно описывая ход вашего решения: Построить полигон распределения. Вычислить выборочную среднюю, дисперсию, моду, медиану. Построить выборочную функцию распределения. Построим дискретный вариационный ряд. Для этого подсчитаем количество повторения для каждого элемента ряда.
Таблица для расчета показателей.
Построим полигон распределения, для этого на оси абсцисс отметим значения случайной величины, а на оси ординат – частоты значений случайной величины (кол-во повторений в ряду) и соединим точки линиями, получим: 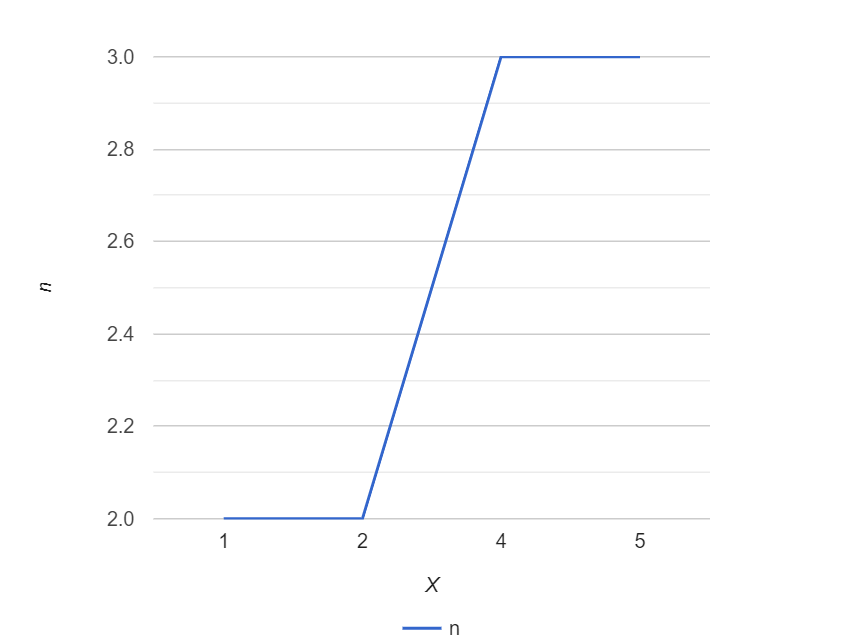 Рассчитаем выборочную среднюю (среднюю взвешенную): Дисперсия случайной величины найдём по формуле, значения возьмём из расчётной таблицы: Мода - наиболее часто встречающееся значение признака у единиц данной совокупности. Имеются два показателя с одинаковым значением частоты f=3. Ряд имеет две моды, т.е. является бимодальным. Медиана. Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим xi, при котором накопленная частота S будет больше ∑f/2 = 6. Это значение xi = 4. Таким образом, медиана равна 4. Построим выборочную (эмпирическую) функцию распределения. Для этого возьмём данные из колонки «Относительная частота» расчётной таблицы и подсчитаем значения F(x): F(x) = 0, при x<1 F(x) = 0.2, при 1 F(x) = 0.2+0.2=0.4, при 2 F(x) = 0.4+03=0.7, при 4 F(x) = 0.7+0.3=1, при x>5 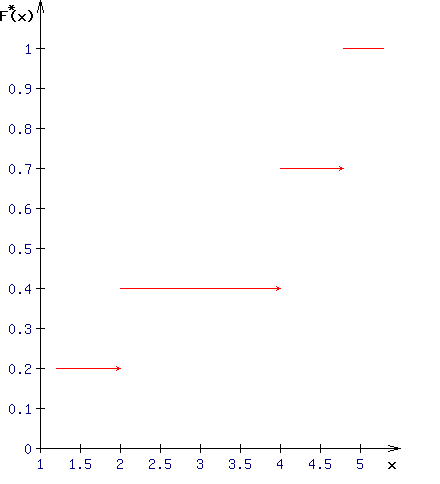 |
