Курсовая (1). Программная реализация и анализ алгоритмов поиска в тексте
 Скачать 1.83 Mb. Скачать 1.83 Mb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный педагогический университет им. Л. Н. Толстого» (ФГБОУ ВО «ТГПУ им. Л. Н. Толстого») Кафедра информатики и информационных технологий КУРСОВАЯ РАБОТА по дисциплине «Структуры и алгоритмы компьютерной обработки данных» на тему: «Программная реализация и анализ алгоритмов поиска в тексте» Выполнил: студент(ка) 2 курса группы 120881 факультета математики, физики и информатики направления «Математическое обеспечение и администрирование информационных систем» профиля «Информационные системы и базы данных» Корнев____________________________ Научный руководитель: к.п.н., доцент Ваныкина Г.В. Тула 2020 Содержание1.2.1 Прямой поиск 12 1.2.2 Алгоритм Кнута, Морриса и Пратта 15 ВВЕДЕНИЕ Задачи поиска слова в тексте используются в криптографии, различных разделах физики, сжатии данных, распознавании речи и других сферах человеческой деятельности. Люди, которые часто работают в текстовых редакторах, знают насколько уникальная вещь, которая позволяет находить нужные слова, а так же целые предложения, в тексте. Одна из причин, это возможность производить быстрый поиск нужной информации. Берем тот же самый Microsoft Office Word, в котором есть такая удобная возможность, как поиск и замена фрагментов. При работе с большими документами это просто необходимо. Безусловно, сейчас функции поиска встроены во все текстовые редакторы, но при этом, они не всегда написаны лучшим образом. Возможен такой вариант, что используются не самый эффективный алгоритм. Область применения функции поиска не ограничивается одними лишь текстовыми редакторами. Следует отметить использование алгоритмов поиска так же возможен в обычных html – страницах. С учетом того, что многие форматы, такие как: Word, Exel, PDF, и тому подобные, уже можно открывать в обычном браузере, применение поиска в тексте становится более обширным. Работа простейшего спам – фильтра, заключается в нахождении в тексте письма фраз таких, как «Миллион за час» или «Раскрутка сайта». Все вышесказанное говорит об актуальности проблемы, затрагиваемой работой. В данной работе мы ставим цель, выявить наиболее оптимальный алгоритм, решающий поставленную задачу поиска. Задачи данной работы: Рассмотреть основные алгоритмы, решающие задачу поиска; Выявить эффективные, с точки зрения времени выполнения, алгоритмы. Работа содержит две основных части. В первой будут рассмотрены алгоритмы, их теоретическое обоснование, алгоритмическая модель, будет проведена попытка их классификации. Во второй части работы будут приведены данные о практическом применении алгоритмов. В заключении будет сделан вывод о наиболее эффективном (с временной точки зрения) алгоритме. ГЛАВА 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПОИСКА В ТЕКСТЕ 1.1 Основные понятия в области поиска в тексте Все определения были взяты из [1] • Алфавит – конечное множество символов. • Длина строки – количество знаков в строке. • Строка (слово) – это последовательность символов из некоторого алфавита. Длина строки – количество символов в строке. Строку будем обозначать символами алфавита, например  – строка длинной n, где – строка длинной n, где 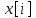 – i-ый символ строки Х, принадлежащий алфавиту. Строка, не содержащая ни одного символа, называется пустой. – i-ый символ строки Х, принадлежащий алфавиту. Строка, не содержащая ни одного символа, называется пустой.• Строка X называется подстрокой строки Y, если найдутся такие строки  и и 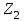 , что , что  . При этом . При этом  называют левым, а называют левым, а 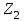 – правым крылом подстроки. Подстрокой может быть и сама строка. Иногда при этом строку X называют вхождением в строку Y. Например, строки hrf и fhr является подстроками строки abhrfhr. – правым крылом подстроки. Подстрокой может быть и сама строка. Иногда при этом строку X называют вхождением в строку Y. Например, строки hrf и fhr является подстроками строки abhrfhr.• Подстрока X называется префиксом строки Y, если есть такая подстрока Z, что  . Причем сама строка является префиксом для себя самой (так как найдется нулевая строка L, что . Причем сама строка является префиксом для себя самой (так как найдется нулевая строка L, что  ). Например, подстрока ab является префиксом строки abcfa. ). Например, подстрока ab является префиксом строки abcfa.• Подстрока X называется суффиксом строки Y, если есть такая подстрока Z, что 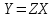 . Аналогично, строка является суффиксом себя самой. Например, подстрока bfg является суффиксом строки vsenfbfg. . Аналогично, строка является суффиксом себя самой. Например, подстрока bfg является суффиксом строки vsenfbfg.1.2 Алгоритмы поиска в тексте и их классификации Рассмотрим несколько известных алгоритмов поиска подстроки в строке, а именно «Алгоритм прямого поиска», «Алгоритм Кнута, Морриса и Пратта» и «Алгоритм Бойера и Мура» Основная идея алгоритма прямым поиском заключается в посимвольном сравнении строки с подстрокой. Алгоритм прямого поиска является малозатратным и не нуждается в предварительной обработке и в дополнительном пространстве. Алгоритм Кнута, Морриса и Пратта основывается на том, что после частичного совпадения начальной части подстроки с соответствующими символами строки можно, вычислить сведения, с помощью которых быстро продвинуться по строке. Трудоемкость алгоритма Кнута, Морриса и Пратта лучше, чем трудоемкость алгоритма прямого поиска. Особенность алгоритма Бойера и Мура заключается в предварительных вычислениях над подстрокой с целью сравнения подстроки с исходной строкой, осуществляемой не во всех позициях. Алгоритм Бойера и Мура оптимален в большинстве случаев, когда нет возможности провести предварительную обработку текста, в котором проводится поиск. Традиционно в программировании понятие сложности алгоритма связано с использованием ресурсов компьютера: насколько много процессорного времени требует программа для своего выполнения, насколько много при этом расходуется память машины? Учет памяти обычно ведется по объему данных и не принимается во внимание память, расходуемая для записи команд программы. Время рассчитывается в относительных единицах так, чтобы эта оценка, по возможности, была одинаковой для машин с разной тактовой частотой. [2] Под трудоемкостью алгоритма А на входе D будем понимать количество элементарных операций, которые учитываются при анализе алгоритма. Под худшим случаем трудоемкости понимают наибольшее количество операций, задаваемых алгоритмом А на всех входах D определенной размерности n. Определим лучший случай трудоемкости, как наименьшее количество операций в аналогичном алгоритме и при той же размерности входа. Средний случай трудоемкости определяется средним количеством операций рассматриваемого алгоритма и входных данных. Зависимость трудоемкости алгоритма А от значения параметров на входе D определяет функцию трудоемкости алгоритма А для входа D. [1] Классический анализ алгоритмов в данном контексте связан, прежде всего, с оценкой временной сложности. Большинство алгоритмов имеют основной параметр, который в значительной степени влияет на время выполнения операций. Если же определяющих параметров несколько, то, как правило, один их них выражается как функция от остальных. Иногда используют и такой подход: рассматривают только один параметр, считая остальные константами. [1] Результатом анализа является асимптотическая оценка выполняемых алгоритмом операций в зависимости от длины входа, которая указывает порядок роста функции и результаты сравнения работы алгоритмов для больших данных. При этом оценка на реальных данных отличается от асимптотической тем, что она ориентирована на конкретные длины входов и число выполняемых алгоритмом операций. Временная сложность алгоритма определяется асимптотической оценкой функции трудоемкости алгоритма для худшего случая, обозначается  и читается как «О большое» или «О-нотация». Асимптотический класс функций О включает в себя как средний, так и лучший случай, потому что запись и читается как «О большое» или «О-нотация». Асимптотический класс функций О включает в себя как средний, так и лучший случай, потому что запись  обозначает класс функций, скорость роста которых не более, чем обозначает класс функций, скорость роста которых не более, чем 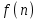 с точностью до некоторой положительной константы. В зависимости от вида функции с точностью до некоторой положительной константы. В зависимости от вида функции 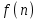 выделяют следующие классы сложности алгоритмов. [1] выделяют следующие классы сложности алгоритмов. [1]Классы сложности алгоритмов в зависимости от функции трудоемкости
На основании математических методов исследования асимптотических функций трудоемкости на бесконечности выделены пять классов алгоритмов. Класс π0 – это класс быстрых алгоритмов с постоянным временем выполнения, их функция трудоемкости 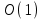 . Промежуточное состояние занимают алгоритмы со сложностью . Промежуточное состояние занимают алгоритмы со сложностью  , которые также относят к данному классу. , которые также относят к данному классу.Класс πР – это класс рациональных или полиномиальных алгоритмов, функция трудоемкости которых определяется полиномиально от входных параметров. Например,  , , 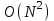 , ,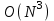 . .Класс πL – это класс субэкспоненциальных алгоритмов со степенью трудоемкости  . .Класс πE– это класс собственно экспоненциальных алгоритмов со степенью трудоемкости  . .Класс πF– это класс собственно надэкспоненциальных алгоритмов. Существуют алгоритмы с факториальной трудоемкостью, но они в основном не имеют практического применения. Состояние памяти при выполнении алгоритма определяется значениями, требующими для размещения определенных участков. При этом в ходе решения задачи может быть задействовано дополнительное количество ячеек. Под объемом памяти, требуемым алгоритмом А для входа D, понимаем максимальное количество ячеек памяти, задействованных в ходе выполнения алгоритма. Емкостная сложность алгоритма определяется как асимптотическая оценка функции объема памяти алгоритма для худшего случая. Таким образом, ресурсная сложность алгоритма в худшем, среднем и лучшем случаях определяется как упорядоченная пара классов функций временной и емкостной сложности, заданных асимптотическими обозначениями и соответствующих рассматриваемому случаю. [1] |

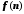
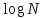
 , если основание равно 10, или порядка 10, если основание равно 2; когда N=1 000 000, значения
, если основание равно 10, или порядка 10, если основание равно 2; когда N=1 000 000, значения  .
.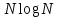
 . Когда N удваивается, тогда время выполнения более чем удваивается.
. Когда N удваивается, тогда время выполнения более чем удваивается.