Курсовая (1). Программная реализация и анализ алгоритмов поиска в тексте

• Название: Программная реализация и анализ алгоритмов поиска в тексте
• Дата: 09.11.2020
• Размер: 1.83 Mb.
• Имя файла: Курсовая (1).docx
• Тип: Курсовая; #149201
• страница: 3 из 5

1.2.2 Алгоритм Кнута, Морриса и Пратта

Алгоритм был открыт Д. Кнутом и В. Праттом и, независимо от них, Д. Моррисом. Результаты своей работы они совместно опубликовали в 1977 году. Алгоритм Кнута, Морриса и Пратта (КМП-алгоритм) является алгоритмом, который фактически требуюет только 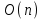сравнений даже в самом худшем случае. Рассматриваемый алгоритм основывается на том, что после частичного совпадения начальной части подстроки с соответствующими символами строки фактически известна пройденная часть строки и можно, вычислить некоторые сведения, с помощью которых затем быстро продвинуться по строке.

Основным отличием алгоритма Кнута, Морриса и Пратта от алгоритма прямого поиска заключается в том, что сдвиг подстроки выполняется не на один символ на каждом шаге алгоритма, а на некоторое переменное количество символов. Следовательно, перед тем как осуществлять очередной сдвиг, необходимо определить величину сдвига. Для повышения эффективности алгоритма необходимо, чтобы сдвиг на каждом шаге был бы как можно большим (рис. 2). На рисунке символы, подвергшиеся сравнению, выделены жирным шрифтом.

Если для произвольной подстроки определить все ее начала, одновременно являющиеся ее концами, и выбрать из них самую длинную (не считая, конечно, саму строку), то такую процедуру принято называть префикс-функцией. В реализации алгоритма Кнута, Морриса и Пратта используется предобработка искомой подстроки, которая заключается в создании префикс-функции на ее основе. При этом используется следующая идея: если префикс (он же суффикс) строки длинной i длиннее одного символа, то он одновременно и префикс подстроки длинной 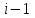. Таким образом, проверяем префикс предыдущей подстроки, если же тот не подходит, то префикс ее префикса, и т.д. Действуя так, находим наибольший искомый префикс.

i

i

i

i

Строка

A

B

C

A

B

C

A

A

B

C

A

B

D

Подстрока

A

B

C

A A

B B

D C

A A

B B A

D C B

A C

B A

D B

D

Рис.2. Демонстрация алгоритма Кнута, Морриса и Пратта [8]

//описание функции алгоритма Кнута, Морриса и Пратта

int KMPSearch(char *string, char *substring){

int sl, ssl;

int res = -1;

sl = strlen(string);

ssl = strlen(substring);

if ( sl == 0 )

cout << "Неверно задана строка\n";

else if ( ssl == 0 )

cout << "Неверно задана подстрока\n";

else {

int i, j = 0, k = -1;

int *d;

d = new int[1000];

d[0] = -1;

while ( j < ssl - 1 ) {

while ( k >= 0 && substring[j] != substring[k] )

k = d[k];

j++;

k++;

if ( substring[j] == substring[k] )

d[j] = d[k];

else

d[j] = k;

}

i = 0;

j = 0;

while ( j < ssl && i < sl ){

while ( j >= 0 && string[i] != substring[j] )

j = d[j];

i++;

j++;

}

delete [] d;

res = j == ssl ? i - ssl : -1;

}

return res;

}

Точный анализ рассматриваемого алгоритма весьма сложен. Д. Кнут, Д. Моррис и В. Пратт доказывают, что для данного алгоритма требуется порядка 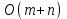сравнений символов (где n и m – длины строки и подстроки соответственно), что значительно лучше, чем при прямом поиске. [1]