ПРОГРАММНАЯ РЕАЛИЗАЦИЯ СПЕКТРАЛЬНОГО ОЦЕНИВАНИЯ ПО МЕТОДУ МИНИМУМА ДИСПЕРСИИ. ДипМинДисп2. Программная реализация спектрального оценивания по методу минимума дисперсии
 Скачать 281 Kb. Скачать 281 Kb.
|
b [n-p] ( 24 )
b [n] = - a bk,p x[ n+k] ( 23 )
означает оценку, а индекс f используется для обозначения оценки, осуществляемой вперед. Второй нижний индекс в обозначении коэффициента a fk,p говорит о том, что количество весовых коэффициентов равно p. Предсказание вперед понимается здесь в том смысле, что оценка, соответствующая временному индексу n , вычисляется по p предыдущим отсчетам случайного процесса. Ошибка предсказания впередПРОГРАММНАЯ РЕАЛИЗАЦИЯ СПЕКТРАЛЬНОГО ОЦЕНИВАНИЯ ПО МЕТОДУ МИНИМУМА ДИСПЕРСИИ Цель: разработка программы позволяющей проводить сравнительный анализ нелинейного метода спектрального оценивания с известными линейными алгоритмами . Программа должна иметь удобный интерфейс для ее использования в учебном процессе. 1.ВВЕДЕНИЕ.Большое количество задач сводится к оцениванию спектра на основе ограниченного набора данных. Раздел науки в котором рассматриваются подобные вопросы называется спектральным анализом. Преобразование Фурье является математической основой для решения задач спектрального анализа, и оно связывает временной сигнал ( или последовательность отсчетов сигнала – если рассматриваются дискретные выборки значений сигнала ) и его представление в частотной области. Однако основная проблема заключается в том, что сигналы ( спектр которых измеряется) являются случайными. При этом доступен для вычисления спектра ( или спектрального анализа ) только небольшой временной отрезок данного сигнала. И основная задача спектрального анализа – по отрезку реализации случайного процесса необходимо максимально точно оценить истинный спектр. В настоящее время известно множество методов решения подобной задачи. Их можно разделить на 2 категории – линейные и нелинейные. В данной работе рассматривается разработка программного продукта в котором производится сравнительный анализ ряда линейных алгоритмов и нескольких нелинейных ( современных но недостаточно исследованного ). 2.ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ Как говорилось выше математической основой вычисления спектра является преобразование Фурье + S ( j w ) = x(t) e – j w t dt ( 1 ) - Наибольший практический интерес представляет модуль этой функции |S ( j w ) | , который является амплитудным спектром сигнала. И этот амплитудный спектр несет информацию о частотах гармонических колебаний составляющих ( в совокупности ) данный сигнал. Как правило, сигнал имеет ограниченную длительность, поэтому вместо формулы ( 1 ) можно записать Тсигн S ( j ) = x(t) exp( - j t ) d t ( 2 ) 0 Здесь считается, что сигнал ограничен во времени от 0 до Тсигн . Часто принято использовать обыкновенную частоту ( в герцах ) и циклическую . Они связаны соотношением = 2 f . (3) Поэтому формулу ( 2 ) можно переписать в виде Тсигн S ( j f ) = x(t) exp( - j 2 f t ) d t . ( 4 ) 0 При использовании цифровой вычислительной техники вместо вычисления интеграла можно использовать суммирование если дискретизировать сигнал x(t) с достаточно малым шагом T. Как выбрать шаг дискретизации, чтобы сохранить всю информацию о непрерывной функции x(t). Ответ на этот вопрос следует из теоремы Котельникова Tдискр < 1 / ( 2 f max ) ( 5 ) Здесь f max - максимальная частота спектра сигнала. Таким образом, можно вместо непрерывного сигнала использовать массив чисел – выбранных значений данного сигнала. И дискретное преобразование Фурье записывается следующим образом N -1 S( j f )x[ n ] exp ( - j2 fTдискр n ) ( 6 ) n = 0 Здесь f изменяется от 0 до 1/ Tдискр . Опять же формулу ( 6 ) часто записывают в несколько ином виде (более компактном и удобном виде ) N -1 S( j x[ n ] exp ( - j n ) ( 7 ) n=0 Здесь 2 f fдискр - дискретная частота и основной интервал дискретной частоты от - доДело в том, что если присмотреться к (7), то мы увидим, что S( j периодическая функция с периодом 2 . Для лучшего понимания дальнейших алгоритмов рассмотрим следующую задачу . Задан сигнал x(t) = cos ( 2 fс t ) , при 0 < t < L Tс, ( 8 ) при других значениях t сигнал равен 0. В ( 8 ) fс = 1 / Tс, fс = 100 Гц, Tс - период косинусоиды, fс - частота косинусоиды, L – количество периодов косинусоиды из которых состоит наш сигнал. Необходимо вычислить спектр данного сигнала. Как видно сигнал – это отрезок ( L периодов ) фукции соs. Вычисляем спектр данного сигнала . Если аналитически вычислить преобразование Фурье, а затем построить спектр, то получим следующую приближенную зависимость ( чем больше L, тем она точнее ) | S( j f) | = L sin ( L Tc [ f - fс ] ) / ( [f - fс ] )   Рис. 1| S( j f) |        0 f Спектр данного сигнала формально не имеет граничной частоты, т.е. продолжается до бесконечности. Однако он достаточно быстро стремится к 0. При этом если L велико ( в пределе бесконечность ) , то спектр сигнала представляет одну ( дискретную ) гармонику на частоте fс . Однако при приеме мы часто располагаем не всей его длительностью, а частью ( не всеми L периодами , а лишь несколькими ). Далее в следующем примере эта задача реализуется в конкретной программе. 2.1 Пример Как видно из рис.1 модуль спектральной плотности мощности достаточно быстро уменьшается после fс . Поэтому приближенно будем считать, что практически вся энергия сигнала будет сосредоточена на частотах от 0 до 10 fс . Это вполне справедливо даже при небольших значениях L. В этом случае в соответствие с теоремой Котельникова можно выбрать шаг Tдискр = 1 / [2 *10 * fс ] = 0.0005 c . Заменим непрерывный сигнал дискретным и схема вычисления дискретного преобразования Фурье выглядит следующим образом Цикл по частоте f от 0 до ( fдискр/2 - как сказано выше это максимальная частота в спектре сигнала) сшагом ( fдискр/2 ) / 500 , где 500-количество точек выводимых на график зависимости спектра от частоты N -1 S( j f x[ n ] exp ( - j2fTдискр n ) ( 9 ) n = 0 Завершение цикла Далее приводится текст программы из файла p_posl1.cpp. Выполняемые файлы : p_posl1.exe ( при L=3 ) p_posl2.exe ( при L=90 ). #include "model.h" #include void disk_spectr( void ); void form( void ); // массив в котором будет формироваться реализация сигнала float x[5000]; // массив в котором будет формироваться спектр реализации сигнала float spectr[560]; // f_s – частота сигнала в герцах, T_diskr - шаг (период) дискретизации в секундах // T_s – период функции косинус // L - число периодов косинусоиды в сигнале float T_s = 0.01 , T_diskr , f_diskr, f_s; int N ; // N – число дискретных отсчетов рассматриваемого сигнала int L = 5 ; void main ( void ) { T_diskr = 1 / (2* 10* f_s ); f_diskr = 1 / T_diskr ; N = T_s / T_diskr * L; form(); // функция формирующая реализацию сигнала disk_spectr(); // функция вычисляюшая спектр сигнала Init_graph(); graf_1("spektr", spectr, 0,499 ); Close_graph(); } void form ( void ) { int i; for ( i = 0 ; i < N ; i++ ) x[i] = x[i] + cos(2*PI* f_s * i* T_diskr ); } void disk_spectr( void ) { int i, n; float ww , max ,df , shag ; complex mnoz , sym ; shag = (f_diskr/2) / 500; // Шаг по частоте при вычислении спектра for ( i = 0 ; i < 500 ; i++ ) // Весь интервал частот ( положительных ) // разбивается на 500 точек { tetta= 2*PI* i * shag / f_diskr ; sym= complex( 0,0); for ( n = 0 ; n < N ; n++) { mnoz = complex( cos( -tetta*n),sin( -tetta*n)); sym = sym + x[n]*mnoz ; } spectr[i] = abs( sym ); } max = spectr[0] ; for ( i =1 ; i< 500 ; i++ ) { if ( spectr[i] > max ) max = spectr[i] ; } for(i=0 ; i < 500 ; i++ ) spectr [i] = 20*log10(spectr [i] / max ); } Из сопоставления результатов работы программы при L=90 и L=3 можно сделать следующий вывод. Если нам доступен для наблюдения не весь сигнал, а только его часть, то спектр при этом отличается ( часто достаточно существенно ) от истинного. Дальнейшие исследования решают проблему повышения точности измерения спектра когда нам доступен только короткий фрагмент сигнала. 3. ЛИНЕЙНЫЕ МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА До настоящего момента мы принимали, что сигнал – это детерминированный процесс. Однако реальные сигналы и помехи представляют случайные процессы и в этом случае вычисление спектра несколько иное. Далее приводятся методы вычисления спектра ( для случайных процессов спектр имеет другое название – спектральная плотность мощности ) в предположении, что сигналы это случайные процессы. Существуют два метода определения спектральной плотности мощности. Один метод основан на соотношении ( формула 4.33 по книге Марпл “Цифровой спектральный анализ”) P( R[m] exp ( - jm ) ( 10 ) m= Здесь дискретная частота 2 f / f дикр, R[m] – корреляционная функция случайного процесса. P( спектральная плотность мощности . Как видно из (10) Фурье-преобразование вычисляется не от сигнала ( который является случайным ), а от корреляционной функции этого сигнала R[m] = М { X(n) X(n+m) } ( 10а ) где М – обозначение математическое ожидание , X(n) – значение случайного процесса ( представляющего сигнал ) в момент времени n, а X(n+m) - значение случайного процесса в момент времени n+m . Допущение об эргодичности исследуемого процесса позволяет ввести другое определение спектральной плотности мощности (формула 4.58 по книге Марпл “Цифровой спектральный анализ”) N P() = lim M { 1 / [2N+1] | x[n] exp (- jn ) | 2 } ( 11 ) N-> n=-N где n – номер отсчета исследуемого процесса, M{ …} – обозначение математического ожидания. В соответствие с этими определениями существуют два метода основных – коррелограммный метод и метод периодограмм . 3.1. КОРРЕЛОГРАММНЫЙ МЕТОД ОЦЕНКИ СПМ Использование данного метода заключается ( стр.190 в книге Марпла “Цифровой спектральный анализ”) в подстановке в (10) конечной последовательности оценок корреляционной функции L P( W m )R[ m ] exp ( - jm ) ( 12 ) m = - L В ( 12 ) введена оконная функция служащая для уменьшения смещения оценки. Одно из наиболее популярных окон – это окно Бартлетта ( или треугольное окно ) W(n) = 1 – | m | / L . ( 12a ) Дело в том, что мы практически никогда не располагаем всей корреляцинной функцией, а только фрагментом из 2L+1 отсчета. Далее приводится программа реализующая коррелограммный метод оценки спектральной плотности случайного процесса ( программа p_posl3.cpp и выполняемый файл p_posl3.exe). В ней можно выбрать вид окна ( для взешивания отсчетов корреляционной функции ) . #include "model.h" #define N 1000 #define L 40 // L - длительность оценки корреляционной функции // N – количество отсчетов реализции случайного процесса #include void form( void ); // Функция, которая формирует массив отсчетов // случайного процесса, по которым в дальнейшем ,будет оцениваться // корреляционная функция void correlation( void ); // Функция, которая будет формировать массив // отсчетов оценки корреляционной функции void window( int nomer ); // Функция, которая будет формировать массив отсчетов функции окна ( 0 – без окна, 1 – треугольное окно, 2 – окно Ханна ). void cor_gramma( void ); // Функция, которая будет формировать массив отсчетов // спектральной плотности мощности в массиве spektr complex x[N]; // массив отсчетов случайного процесса, 1000 – длина массива complex R[L]; // массив отсчетов оценки корреляционной функции float w[ L ]; // массив отсчетов функции окна float spectr[500]; // массив отсчетов спектра float chislo_PI = 3.1415 ; void main ( void ) { form(); correlation(); window(2); cor_gramma(); } void window ( int nomer ) { int m; if ( nomer == 0 ) { for( m=0 ; m <=L ; m++ ) w[m] = 1.0 ; } if ( nomer == 1 ) { for( m=0 ; m <=L ; m++ ) w[m] = 1.0 - (float)m / L ; } if ( nomer == 2 ) { for( m=0 ; m < =L ; m++ ) w[m] = 0.5 + 0.5*cos( 3.14 * m / L ) ; } } // В следующей функции формируются две синусоиды в шуме void form ( void ) { int i; for ( i = 0 ; i < N ; i++ ) x[i] = complex( gauss ( 0, 0.1 ), gauss(0 ,0.1) ) ; for ( i = 0 ; i < N ; i++ ) x[i] = x[i] + 0.2*complex( cos ( PI/5 * i ), sin (PI/5*i) ); for ( i = 0 ; i < N ; i++ ) x[i] = x[i] + 0.2*complex( cos ( PI/3 * i ), sin ( PI/3*i) ); } void correlation( void ) { int m, j ; complex sym ; for ( m = 0 ; m < L ; m++ ) { sym = complex( 0 , 0 ); for ( j = 0 ; j < N ; j++ ) { if( (j+m) < N ) sym = sym + x[j+m ] *conj( x[j] ) ; } R[m] = sym/ (N-m); } } void cor_gramma( void ) { int i, m; float ww ; complex mnoz , sym ; float chis_PI2 = 3.14/2 ; for ( i = 0 ; i < 500 ; i++ ) { ww = 3.14*i/ 500 ; sym= complex( 0,0); for ( m = -L ; m < L ; m++) { mnoz = complex( cos( -ww*m),sin( -ww*m)); if( m < 0 ) sym = sym + conj(R[-m])*w[-m]*mnoz ; else sym = sym + R[m]*w[m]*mnoz ; } spectr[i] = abs( sym ); } Init_graph(); graf_1("graphik", spectr, 0,499 ); Close_graph(); } 4.ПЕРИОДОГРАММНЫЕ ОЦЕНКИ СПМ Этот метод поясняется в известной литературе ( кн. Марпл “ Цифровой спектральный анализ” стр.191 – 192. ). В этом случае по конечной последовательности данных можно вычислить выборочный спектр ( формула 5.31 в кн. Марпл “ Цифровой спектральный анализ” ). N-1 P() = 1 / N | x[n] e (- jn ) | 2 ( 13 ) n=0 где P() – выборочный спектр. Недостатком формулы (13) является появление ложных пиков в спектре в связи со случайностью реализации фрагмента сигнала. Для сглаживания быстрых флуктуаций в оценке спектра Даньелл предложил ( кн. Марпл “ Цифровой спектральный анализ” стр.192.) использовать усреднение по соседним частотам n+K P д( i ) = 1 / [2K +1] P( n) n=i-K Здесь предусматривается, что весь интервал частот ( ) разбивается на отрезки ( точки ). Далее приводится программа реализующая данный алгоритм ( программа p_posl4. cpp и выполняемый файл p_posl4.exe). #include "model.h" #define N 1000 #include void form( void ); void vish( void ); complex x[1000]; float spectr[600]; // Массив для оценки спектра по реализации float spectr_sr[600]; // Массив для усредненной оценки спектра float chislo_PI = 3.1415 ; void main ( void ) { form(); vish(); Init_graph(); graf_1("graphik", spectr_sr, 0,499 ); Close_graph(); } void form ( void ) { int i; for ( i = 0 ; i < N ; i++ ) x[i] = complex( gauss ( 0, 0.01 ), gauss(0 ,0.01) ) ; for ( i = 0 ; i < N ; i++ ) x[i] = x[i] + 2*complex( cos ( PI/7 * i ), sin ( PI/7*i) ); for ( i = 0 ; i < N ; i++ ) x[i] = x[i] + 2*complex( cos ( PI/3 * i ), sin ( PI/3*i) ); } void vish( void ) { int i, m, n , j; float ww ; complex mnoz , sym ; static complex y[100], sp[500] ; float chis_PI2 = 3.14/2 ; for ( i = 0 ; i < 500 ; i++ ) { ww = 3.14*i/ 500 ; sym= complex( 0,0); for ( m = 0 ; m < 1000 ; m++) { mnoz = complex( cos( -ww*m),sin( -ww*m)); sym = sym + x[m]*mnoz ; } spectr[i] = abs(sym)*abs(sym) ; } for(i=0; i < 500 ; i++ ) { spectr_sr[i]=0; for( j =-5 ; j <= 5 ; j++ ) { if( ( (i+j)>=0) && ( (i+j)<500) ) spectr_sr[i] = spectr_sr[i] + spectr[i+j]/11. ; } } } 5. ПАРАМЕТРИЧЕСКИЕ МОДЕЛИ СЛУЧАЙНЫХ ПРОЦЕССОВ. Ранее спектр ( точнее спектральная плотность мощности ) была определена как дискретно-временное преобразование Фурье от бесконечной автокорреляционной последовательности ( или самой реализации сигнала ). Другим альтернативным методом спектрального оценивания является принятие гипотезы, о том какая система породила данную реализацию случайного процесса. На первый взгляд кажется что такая информация является недоступной или достаточно условной. Однако на самом деле всегда имеется некоторая априорная информация для предположения о том, что является источником исследуемого процесса. При этом спектр процесса уже будет определяться как функция параметров модели (описывающей ту систему которая породила этот процесс ). Наиболее общей моделью ( которая описывает практически все встречающиеся на практике детерминированные и случайные процессы ) является ( рис.1 на листе ) модель АРСС ( авторегрессии – скользящего среднего ) p q x[n] = - ak x [ n – k ] + bk u [ n – k ] ( 14 ) k=1 k=0 где x[n] – отсчет реализации наблюдаемого случайного процесса в n-й дискретный момент времени, u[n] – входная последовательность представляющая дискретный белый шум с дисперсией , ak – коэффициенты авторегрессии ( АР – коэффициенты ), bk – коэффициенты скользящего среднего. Напомним, что дискретный белый шум – это случайный процесс с нулевым математическим ожиданием соседние отсчеты которого статистически независимы. Если более упрощенно посмотреть на формулу (14), то формирование очередного выходного (наблюдаемого нами ) случайного отсчета x[n] из предыдущих отсчетов этого процесса x[n-1], x[n-2],…, x[n-p] и набора входных отсчетов дискретного белого шума u[n], u[n-1],u[n-2],… . Из этой общей модели АРСС (14) получаются более простые модели – АР ( авторегрессии ) и СС ( скользящего среднего ). Если СС-параметры положить равными нулю ( за исключением b0 = 1 ), то мы получим модель АР-процесса ( рис.3 на листе ) p x[n] = - ak x [ n – k ] + u [ n ] . ( 15 ) k=1 Если АР-параметры положить равными нулю , то мы получим модель СС-процесса ( рис.2 на листе ) q x[n] = bk u [ n – k ] + b0 u [ n ] . ( 16 ) k=1 Важным для практики является возможность выразить параметры одной из моделей ( АР, СС, АРСС ) через параметры любой из двух других моделей ( при этом порядок модели-замены существенно увеличивается по сравнению с p или q ). Так например если случайный процесс был порожден системой описываемой моделью АРСС ( порядка p=4 и q = 4 ), то его можно описать (с большой точностью) моделью АР порядка p от 25 до 50 ( стр.223 в рассматриваемой книге ). Наибольшее практическое применение имеет АР-модель т.к. известно много эффективных алгоритмов оценивания параметров разработано для АР-моделей. Кроме того, вычислительные трудности при АР-модели значительно меньше трудностей вычисления параметров моделей АРСС и СС. Таким образом, будем считать, что исследуемый процесс ( независимо от системы породившей его) является АР-процессом ( при этом порядок модели может быть достаточно большой p >>1 ) . В связи с этим наша задача заключается в оценке параметров АР-модели и ak при k от 1 до p. ( 17 ) Теперь важный момент . Ранее спектр определялся Фурье-преобразованием - (10) или (11) . Спектр АР-процесса определяется уже параметрами АР-модели (кн. Марпл “ Цифровой спектральный анализ” )  p 2 p 2P(ak exp( -j k ) | ( 18 ) k=1 Дальнейшие рассматриваемые алгоритмы будут по принятой реализации x[n] оценивать параметры АР-процесса ( 17 ), а затем по формуле (18 ) оценивать спектр. Базовым соотношением для определения АР-параметров является уравнение Юла-Уокера ( стр.226 в рассматриваемой книге )       R[0] R[-1] R[-p] 1 R[0] R[-1] R[-p] 1 R[1] R[0] R[-p+1] a1 = … … R[p] R[p-1] R[0] ap В уравнении ( 19 ) R[m] – значение корреляционной функции ( 10а) . Решая уравнение (19) относительно параметров АР-процесса можно далее по ( 18 ) вычислить исследуемый спектр. Учитывая, что матрица в (19) является теплицевой и эрмитовой, то алгоритм Левинсона является наиболее эффективным в вычислительном отношении для решения данной задачи ( стр. 134 по кн. Марпла “Цифровой спекральный анализ” ). Такая методика вычисления спектра предполагает, что известны значения корреляционной функции, а это не так. На практике часто стоит задача по короткой последовательности данных x[n] попытаться получить максимально точную оценку спектра. Решение подобной задачи во многом сходно с задачей линейного предсказания данных рассматриваемой далее. 6. ЛИНЕЙНОЕ ПРЕДСКАЗАНИЕ ДАННЫХ Задачу линейного предсказания данных можно сформулировать следующим образом – по набору принятых отсчетов x[n-1],x[n-2],x[n-3]… случайного процесса необходимо максимально точно предсказать значение отсчета будет после этого ( отсчет который поступит потом – будущем ),т.е. x[n]. В виде соотношения это можно записать следующим образом p x |
e p f [n] = x[n] - x
k=1
где a bk,p – коэффициент линейного предсказания назад, соответствующий индексу k. Здесь


 x T [n] = x [ n ] x [ n – 1] … x [ n – k ]
x T [n] = x [ n ] x [ n – 1] … x [ n – k ]




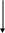


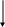
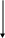


 де
де
 p k 2
p k 2 p
p 