Производственный менеджмент (лекции). Производственный менеджмент
 Скачать 6.27 Mb.
|
|
Теперь наше уравнение принимает следующий вид:  Поскольку все переменные xi и wi принимают целые значения, правая часть уравнения должна быть целочисленной, откуда следует, что левая часть уравнения также должна принимать целые значения. Далее, так как fij 0 и i 0 для всех i и j, то  .Следовательно, выполняется неравенство  .Это означает, что  , поскольку fi < 1.Так как левая часть рассматриваемого неравенства должна принимать целые значения, можно записать необходимое условие ее целочисленности в следующем виде:  .Последнее ограничение перепишем в виде равенства 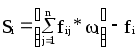 , где Si – неотрицательная дополнительная переменная, которая по определению должна принимать целые значения. Такое ограничение-равенство определяет отсечение Гомори для полностью целочисленной задачи.Из симплексной таблицы следует, что i = 0, и, таким образом, Si = – fi, т. е. данная компонента решения не является допустимой. Это означает, что полученное ранее решение не удовлетворяет новому ограничению. В такой ситуации следует использовать двойственный симплекс-метод, реализация которого обеспечивает отсечение некоторой области многогранника решений, не содержащей точек с целочисленными координатами. Преобразуем исходную таблицу путем приписывания к ней строки и столбца, соответствующих построенному отсечению Гомори для полностью целочисленной задачи. Получим новую таблицу:
Если в результате применения двойственного симплекс-метода решение оказывается целочисленным, то процесс решения исходной задачи завершен. В противном случае необходимо ввести новое отсечение на базе полученной таблицы и вновь воспользоваться двойственным симплекс-методом. Если на некоторой итерации при использовании двойственного симплекс-метода обнаружится отсутствие допустимого решения, то рассматриваемая задача не имеет допустимого целочисленного решения. Название дробный алгоритм связано с тем обстоятельством, что все ненулевые коэффициенты введенного отсечения меньше единицы. Общее число ограничений порожденной задачи не может превышать (m + n). Процесс определения оптимального плана методом Гомори включает следующие этапы: 1. Используя симплекс-метод находят решение задачи без учета требований целочисленности переменных. 2. Составляют дополнительное ограничение для переменной, которая в оптимальном плане имеет максимальное дробное значение, а должна быть целочисленной. 3. Используя двойственный симплекс-метод, находят решение задачи, получающейся в результате присоединения дополнительного ограничения. 4. В случае необходимости составляют еще одно дополнительное ограничение и продолжают процесс. ПРИМЕР F(  ) = 7x1 + 9x2  при ограничениях -x1 + 3x2 6  -x1 + 3 x2 + x3 = 67x1 + x2 35 7x1 + x2 + x4 = 35x1, х2 0, целые; x1, ..., x4 0, целые. Таблица 1
Так как полученное решение не является целочисленным, следует расширить данную таблицу путем введения некоторого отсечения. В качестве производящей строки можно выбрать любую строку таблицы. Обычно выбирается строка, соответствующая  . Сейчас  . Строке с базисной переменной х2 соответствует равенствоx2 + 7/22x3 + 1/22x4 = 7/2. Следовательно, уравнение отсечения Гомори имеет вид - 7/22x3 - 1/22x4 +  = -1/2В результате получаем новую таблицу: Таблица 2
Так как решение опять не является целочисленным, необходимо продолжить процесс введения отсечений. Строке с базисной переменной х1 соответствует ограничение: - 1/7x4 - 6/7 |
=
=