контрольня по мат анализу. Решение Перепишем исходное уравнение в виде. (1)
 Скачать 184 Kb.
|
 Решить матричное уравнение  , где  .Решение: Перепишем исходное уравнение в виде  . (1)Поскольку в правой части уравнения стоит разность матриц 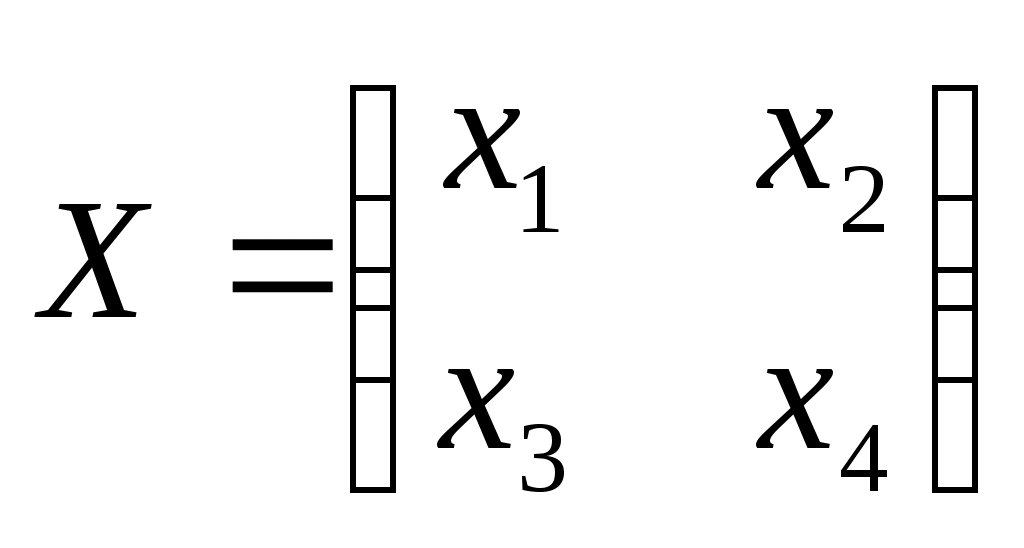 , а вычитать можно только матрицы одинаковой размерности, то искомая матрица имеет вид  .Подставим данное выражение в уравнение (1) и выполним действия над матрицами с учетом того, что 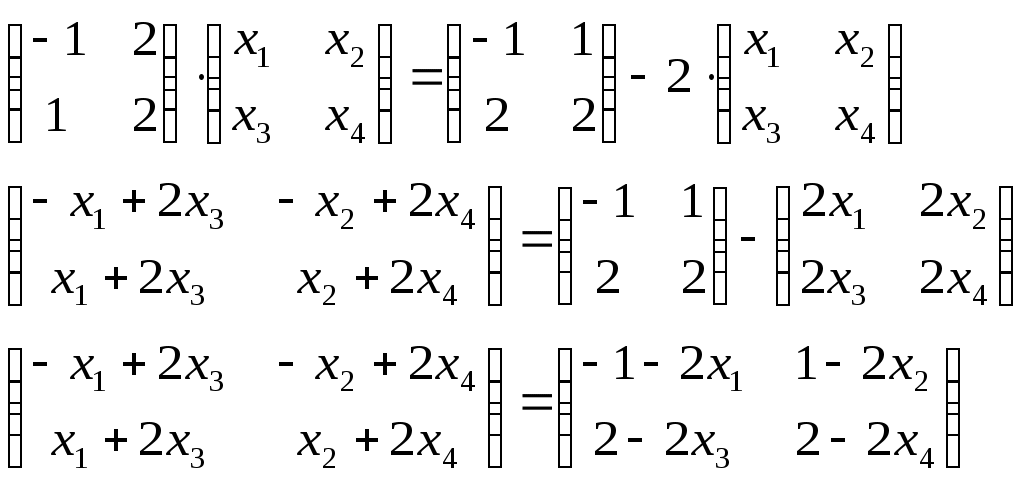 : Поскольку две матрицы равны, когда равны их соответствующие элементы, то полученное равенство запишем в виде системы линейных уравнений: 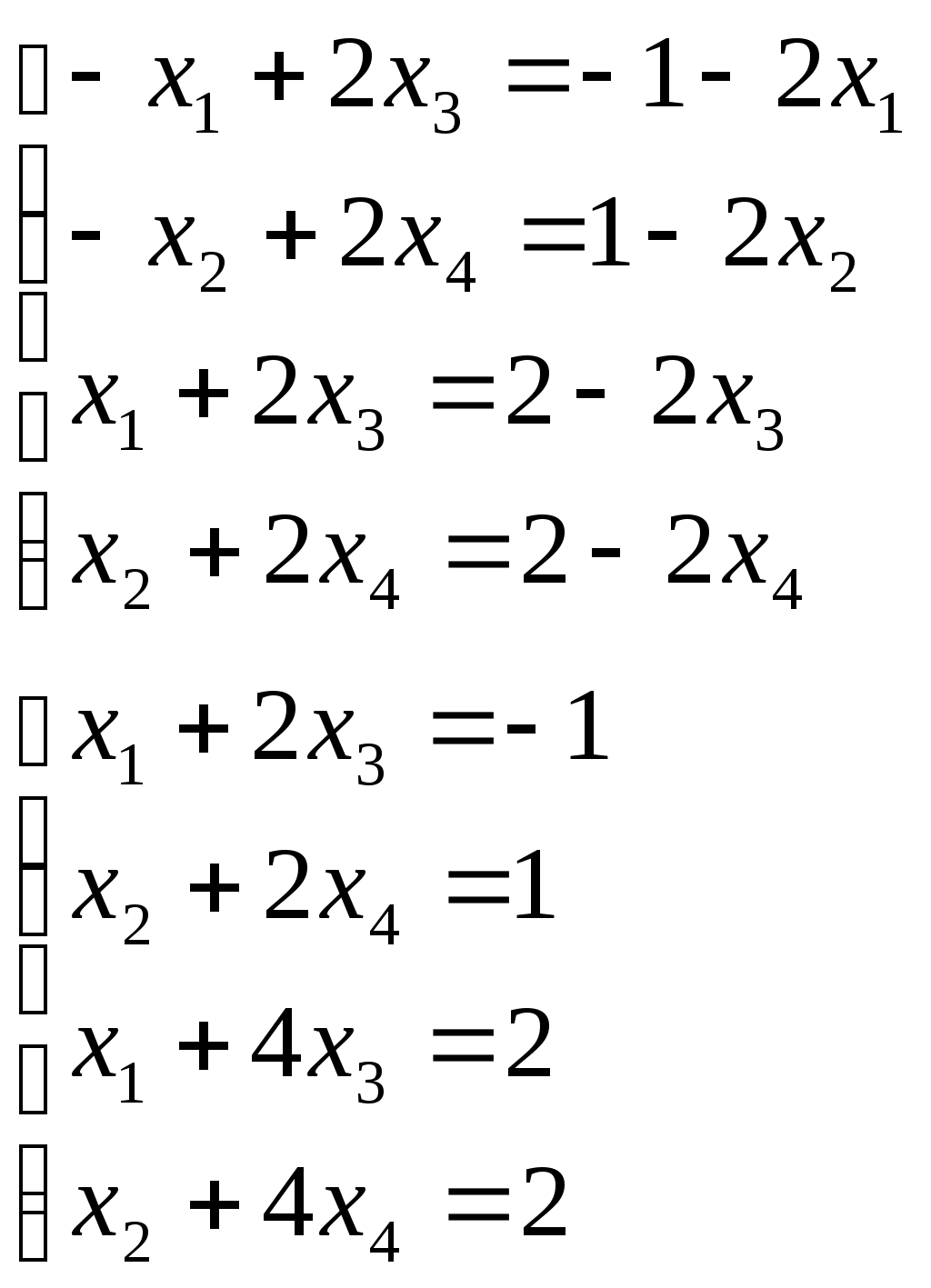 Первое уравнение полученной системы умножим на (-2) и сложим его с третьим. Второе уравнение системы умножим на (-2) и сложим его с четвертым: 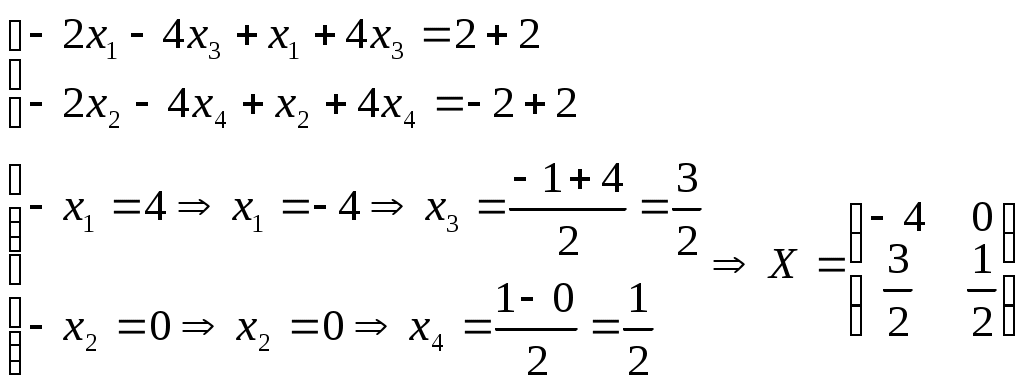 Для проверки полученного решения подставим его в исходное уравнение: 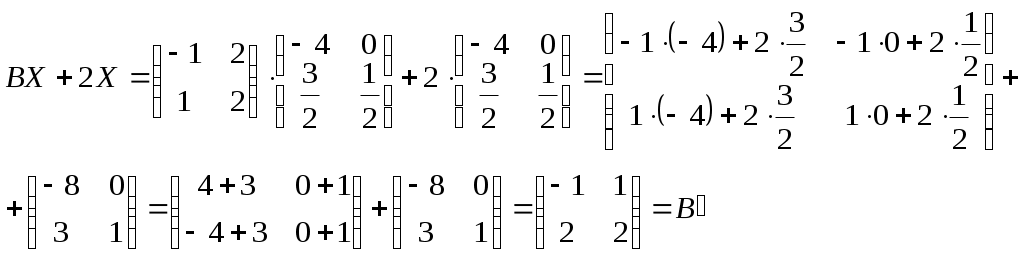 Поскольку при подстановке исходное уравнение превращается в тождество, то решение найдено верно. По формулам Крамера решить систему уравнений 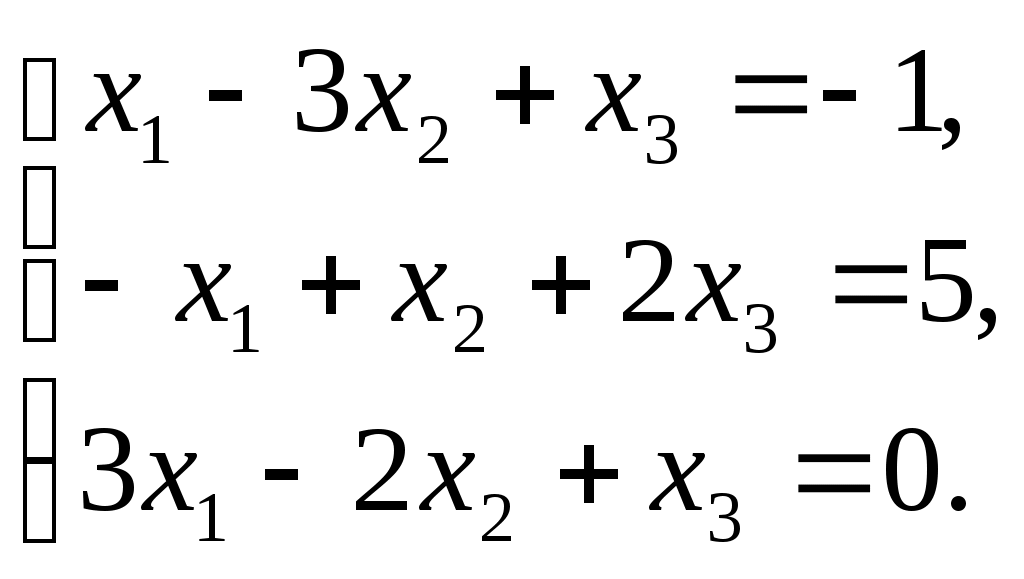 Решение: Вычислим главный определитель (определитель матрицы системы, составленной из коэффициентов, стоящих при неизвестных): 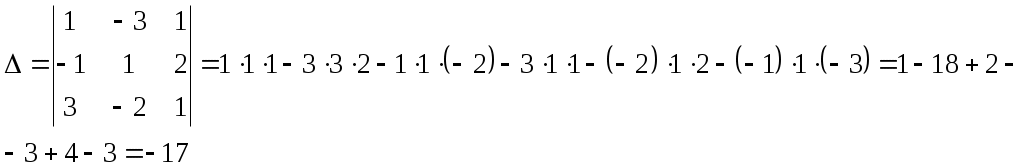 Поскольку 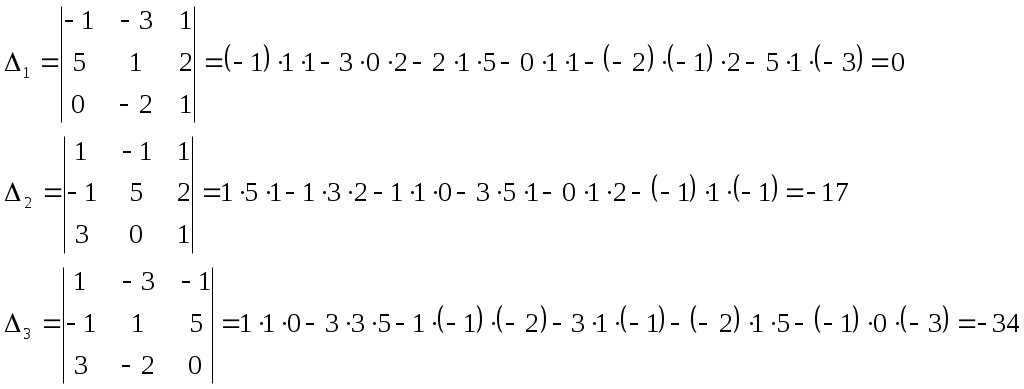 , то для решения данной системы можно использовать формулы Крамера. Вычислим побочные определители, которые получаются из главного определителя при замене столбца коэффициентов при соответствующей неизвестной на столбец свободных членов:  Тогда  ,  ,  .Для проверки найденного решения подставим полученные значения в исходную систему: 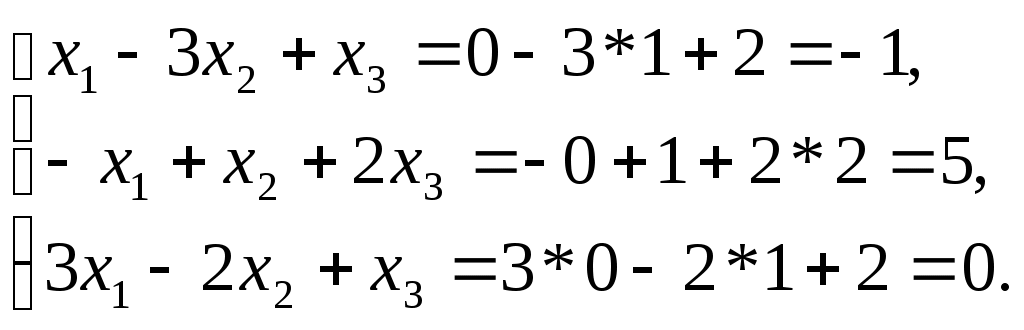 Поскольку при подстановке все уравнения исходной системы обратились в тождества, то решение найдено верно:  ,  ,  .Методом Гаусса решить систему уравнений 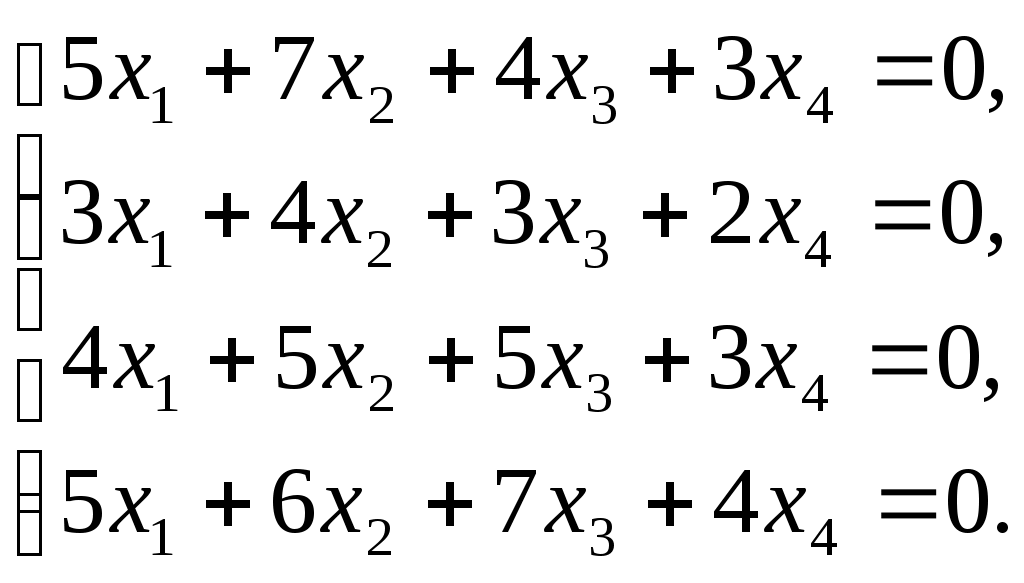 Решение: Прямой ход метода Гаусса: Запишем расширенную матрицу системы и путем эквивалентных преобразований приведем ее к ступенчатому виду:  Элементы первой строки разделим на 5: 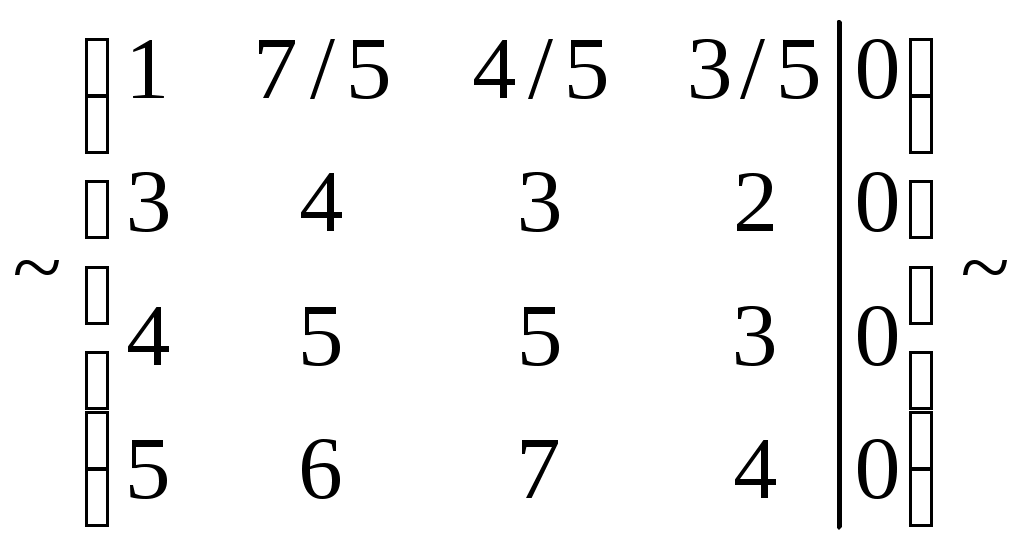 Элементы первой строки умножим на (-3) и прибавим к соответствующим элементам второй строки. Элементы первой строки умножим на (-4) и прибавим к соответствующим элементам третьей строки. Элементы первой строки умножим на (-5) и прибавим к соответствующим элементам четвертой строки: 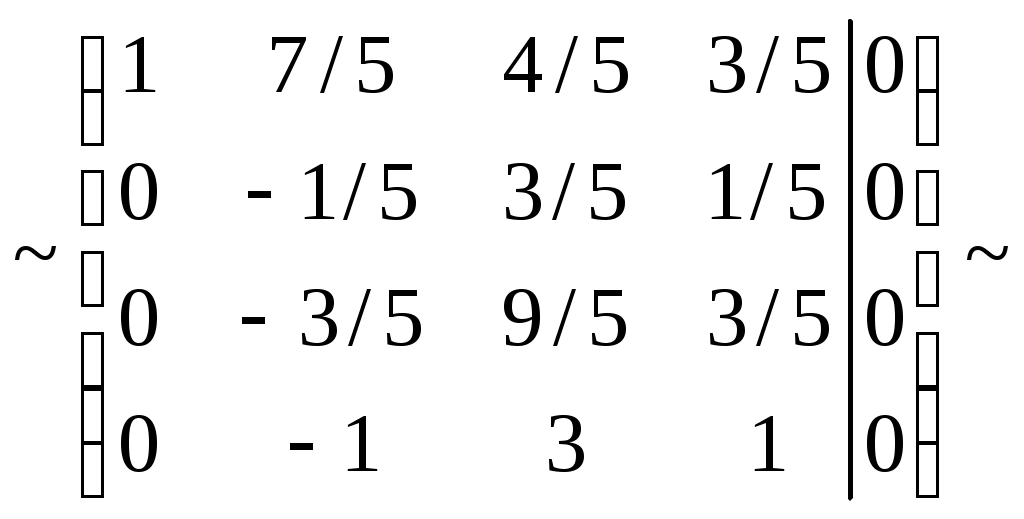 Поскольку вторая, третья и четвертая строки пропорциональны, т.е. линейно зависимы, то удалим любые две из них, например, вторую и третью:  Элементы второй строки разделим на (-1):  Обратный ход метода Гаусса: Поскольку базисный минор 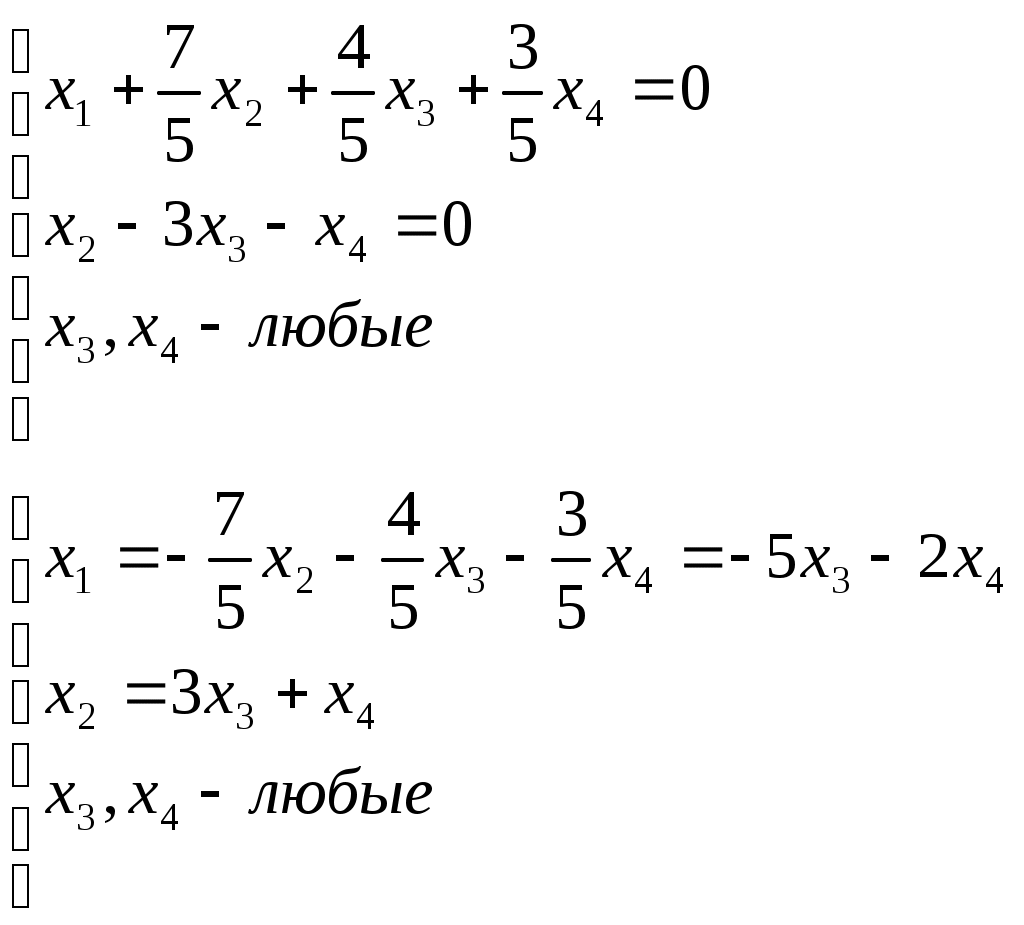 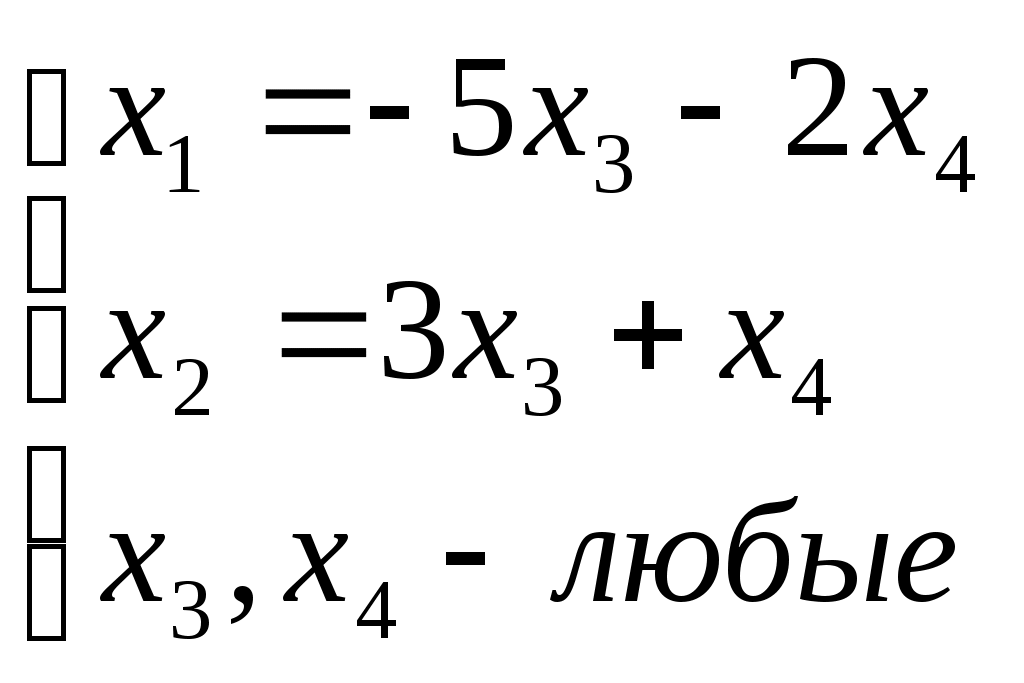находится в первых двух строках, то переменные  ,  – базисные, переменные  ,  – свободные:  – общее решение системыВыполним проверку найденного решения. Для этого полученные выражения подставим в исходную систему: 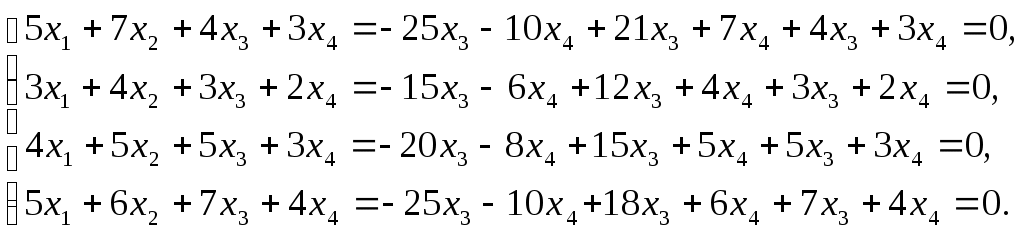 Поскольку при подстановке все уравнения исходной системы обратились в тождества, то решение найдено верно. Найти угол между векторами  и  , если известно, что  ,  ,  ,  , а угол между векторами  и  равен  .Решение: Вычислим скалярное произведение указанных векторов: 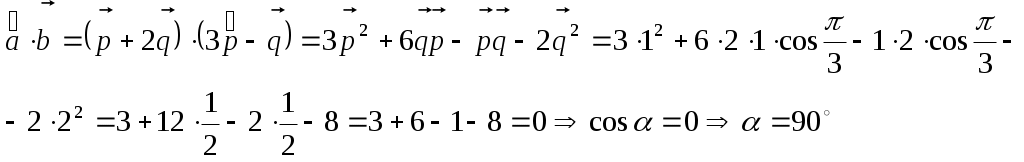 Угол между векторами и  .Определить вид и расположение кривой второго порядка  . Составить уравнение прямой, проходящей через ее центр перпендикулярно прямой  . Сделать чертеж.Решение: Приведем уравнение кривой второго порядка к каноническому виду. Для этого выделим полные квадраты: 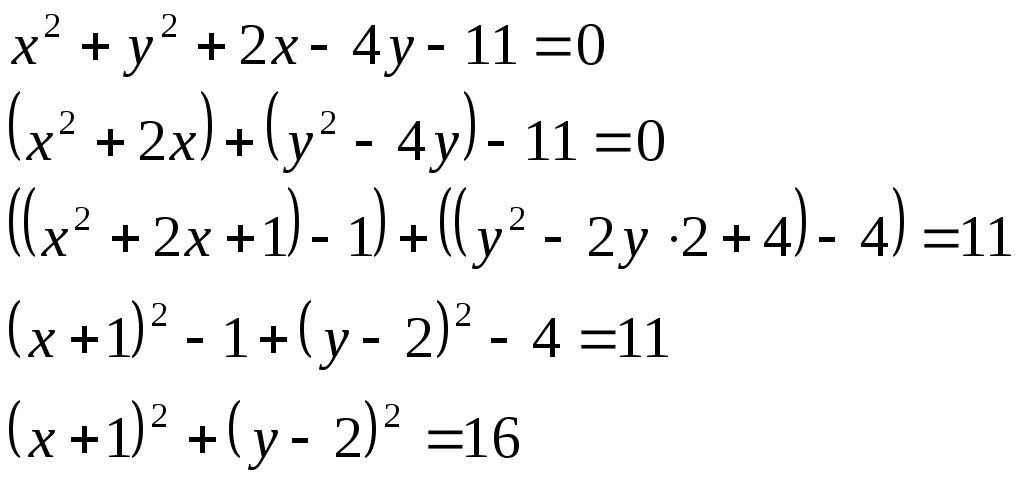  – каноническое уравнение окружности с центром в точке  радиуса  Напишем уравнение прямой, проходящей через точку перпендикулярно прямой . Из данного уравнения прямой запишем координаты ее вектора нормали:  .Поскольку искомая прямая должна быть перпендикулярна данной, то она будет параллельна ее вектору нормали, т.е. вектор можно рассматривать в качестве направляющего вектора искомой прямой, тогда запишем ее уравнение как уравнение прямой, проходящей через заданную точку параллельно заданному вектору:  – каноническое уравнение искомой прямойЗапишем полученное каноническое уравнение в общем виде:   – уравнение искомой прямой в общем видеСделаем чертеж: 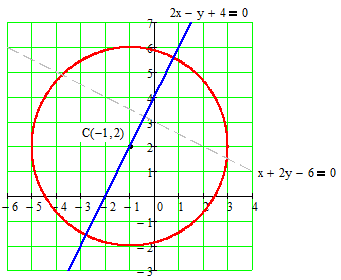 Найти угол между прямой  и плоскостью  .Решение: Для того, чтобы найти угол между прямой и плоскостью, запишем координаты направляющего вектора прямой и вектора нормали к плоскости:  ,  .Тогда  Угол между прямой и плоскостью  .Данная работа скачена с сайта http://www.vzfeiinfo.ru ID работы: 41330 |